几多探究几多“思”——例谈小学生数学探究认知障碍及对策

浙江仙居县实验小学（317300）

数学作为一门较为枯燥、抽象的学科，学生在数学探究认知的过程中障碍重重。要让难题迎刃而解，前期的工作是何等的辛苦，如同在生活中烹食板栗，必须先去掉那层厚厚的刺，才会有之后的清香扑鼻与美味。本文将从认知障碍这个维度选取几个案例，分析原因，寻找对策。

一、图式缺乏障碍

几何知识作为数学基础知识的重要组成部分，一直是基础教育数学课程的重要内容。研究表明，儿童时代是空间知觉即几何直观认知能力的重要发展阶段。小学生学习一些几何初步知识，并在此过程中形成空间观念，对进一步学习几何知识及其他学科知识的影响都是极其重要的。但在具体探究过程中，不少学生对于几何问题往往无从下手，原因就在于学生缺乏相应的图式。譬如在教学平行四边形、三角形、梯形等面积计算时，一般的教学过程是在学生经历面积公式的推导之后，让学生运用面积公式解决图形面积计算问题。如此教法是否能够确保学生已经很好地理解了公式的含义？是否有某些学生的解题活动完全建立在对公式的机械记忆和例题的简单模仿之上呢？事实证明，这种机械模仿的情况是存在的，学生并没有很好地理解公式的含义。

【案例1】请计算下面图形的面积。

学生非常顺利地列出三道算式：8×5÷2，10×8÷2，12×5÷2，可是当教师提问“8×5÷2 求的是三角形的面积，那8×5又如何在图上表示出来呢？”时，却无人能够回答。

形成基理：为什么学生会列式却不明白其中的含义呢？究其原因在于学生的头脑中缺乏相应的图式，之前的公式推导也只是部分学生理解了，而对于大多数学生而言，他们觉得自己要做的只是识记公式。这就给后续组合图形以及空间图形的研究造成知识断层，形成探究障碍。

又如“一本书已经看了58页，还剩下全书的1/4少1页，这本书共有多少页？”，面对此题，多数学生都在绞尽脑汁地想如何解决，也有部分学生在“守株待兔”，等候老师的答案，还有些学生瞎蒙，但没有人通过画线段图来分析该题。皮亚杰认为“图式是人类认识事物的基础”，既然学生没这个基础，也就很难完成探究任务，该题最终还是以教师苦口婆心的讲解收场。

对策：（1）数学思想方法不是一教就会的，而是要在反复中不断体验、感悟得来的。教师在平常教学中应注重数形结合，让学生多进行一些割补、平移等练习。如案例1中，三角形面积公式的推导过程必须由点推广到面，由少数几个学生的汇报推广到同桌互说直至人人过关，这样学生才会理解“三角形面积公式之所以要除以2，是因为底乘高求的是与它等底等高平行四边形的面积，而三角形的面积只是它的一半”，建立这个认知后，学生关于三角形面积计算公式的应用就会更加得心应手。

（2）学生在探究感到困难时，教师可适当增设辅助支架，如上述的书页问题，教师可引导学生一起画线段图，而不是“全盘托出”。“一回生，二回熟”，相信经过一段时间的训练后，学生对线段图一定不会再觉得“高不可攀”了。

二、知识迁移障碍

心理学上把一种学习对另一种学习的影响，称为学习迁移。众所周知，即便是最优秀的教师，也不可能教给学生在任何时候、任何情境中都适用的具体操作。迁移可使学生在学习中不断地掌握知识和发展适应新情境、解决新问题的能力。可见，学习的迁移问题是教学中一个极其重要的问题。根据迁移的性质可把它分为正迁移和负迁移两类，在学生的探究学习过程中，更多碰到的是知识迁移的障碍，即一种学习对另一种学习的阻碍作用。

【案例2】两位数笔算乘法。

师：如果老师分给你们每人86根小棒，请你们算一下一共需要多少根小棒？（全班41人）

生：用 86乘 41就可以了。（板书：86×41）

师：把你的竖式写下来。

形成基理：在这个案例中，我认为学生的直觉判断来自其朦胧而朴素的类比思想，即所谓的张冠李戴，由加法竖式类比乘法竖式，笔算加法的方法是相同数位上的数相加，满十进一，由此推出笔算乘法的方法是相同数位上的数相乘，满几十就向前一位进几。

【案例3】用简便方法计算。

形成基理：这是学完简便运算后，学生常出现的两种错误，究其原因在于他们对乘法结合律和乘法分配律两个概念的混淆，这一混淆为他们想当然的迁移起到“意义支撑”的作用。

对策：两个案例的共通之处在于学生对知识的本质没有一个根本的了解。案例2中，应强调竖式计算方法的依据应是算理，而不是表象，引导学生正确对待知识的负迁移，在探究时运用正、反方摆事实、讲道理的方式建立起正确的问题解决方法。例如，我们可以这样处理：首先把学习的主动权交给学生，要求每个学生根据自己的想法列出竖式，面对不同的竖式势必引发学生的争论，产生寻求统一的动机。“真金不怕火来炼”，有算理“庇护”的学生定能自圆其说，错误列法也就不攻自破。相信这样一个激辩互动的过程定能让学生更好地理解两位数笔算乘法的算理。而案例3，我们可以在澄清基本概念的过程中，对关键字进行比较剖析（见下表）。

（有的学生的竖式是这样的：

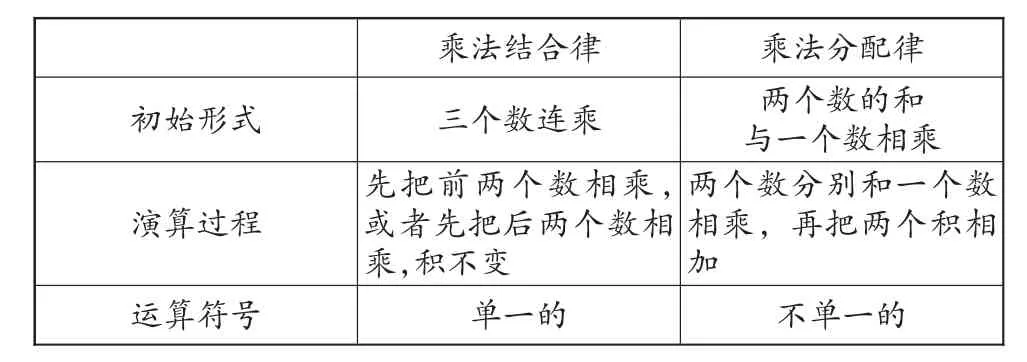
乘法结合律 乘法分配律初始形式 三个数连乘 两个数的和与一个数相乘演算过程两个数分别和一个数相乘，再把两个积相加运算符号 单一的 不单一的先把前两个数相乘，或者先把后两个数相乘，积不变

可见，乘法结合律在演算的过程中一乘到底，即符号是单一的，而乘法分配律最终结果是一个和，即符号是不单一的。为了强化学生的认知，我们可多进行一些混仿练习，在学生算完之后再引导学生比较，唯有比较才能让学生有所悟。

三、阅读理解障碍

阅读是人类社会生活的一项重要活动，是人们汲取知识的主要手段和认识世界的重要途径。数学既是一门科学，同时也是一种文化，更是一种语言。数学阅读是学生个体根据已有的知识经验，通过阅读数学材料建构数学意义和方法的学习活动，是学生主动获取信息、汲取知识、发展数学思维、学习数学语言的重要途径。数学教材讲究的是准确性、概括性和条理性，知识之间联系密切，每一课时的知识编排也有一定的顺序，从准备题、例题、试一试到练习，一成不变，这对学生而言，没有多少新鲜感和吸引力。基于此，不少教师忽略了对学生数学阅读能力的培养，使得学生在执行探究任务的第一步——阅读审题便遇到了障碍。

【案例4】认为以下这组线段能搭成三角形的画“√”，认为不能的画“×”。

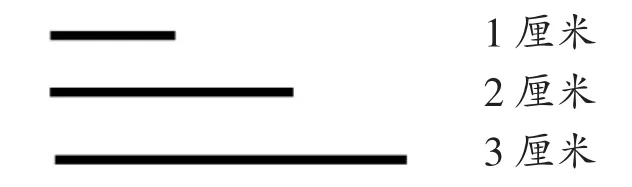
生1：我觉得可以画“√”也可以画“×”。因为“三角形任意两边的和大于第三边”，如果我选1厘米和2厘米，它们的和与第三条相等，就不行；我选2厘米和3厘米，那么它们的和大于1厘米，可行。

生2：黑板上写的是“任意”，那么三种情况中只要有一种不符合，就不能画“√”。

形成基理：学生由于缺失对“任意”一词的完整理解，故而把“任意”一词语义中的某一语义泛化了。“三角形任意两边的和大于第三边”中的“任意”应解释为“任何的，所有的，每”，这和学生生活中接触到的“你可以任意选你想买的东西”中的“随便”解释意义不同。学生的阅读理解能力有限，不能理解不同语境中同一词语的意思，形成阅读理解障碍，困扰了他们的探究。

对策：（1）学生对某些语句不理解时，可尝试让他们大声朗读，或陈述一些与问题有关的信息，培养自我提问的能力；还可以用各种各样的图把问题形象化，如就能帮助学生理解“任意两边之和大于第三边才能围成三角形”。（2）用同样意思却易理解的词来代替说明，如“三角形每两条边的和大于第三边”，这样学生就容易理解了。（3）通过完善学生的经验来达到对相关语义的理解。

如这道题“一台磨面机0.8小时磨面0.5吨。平均每小时可以磨面多少吨？磨一吨面需要几小时？”，两个小数放在一块，究竟谁除以谁，大部分学生对此容易搞错，究其原因是除了学生惯用大数除以小数之外，最主要的是学生对于题中的两个问题在阅读上不是很理解。此时，教师不妨先让学生回答一些简单的问题，如“3个人吃6个苹果，平均每人吃多少个？6÷3=2（个）”“小明20分钟走1千米，平均每分钟走多少千米？1÷20=0.05（千米）”……让学生观察发现每份量跟除数之间的关系，进而明确第一问的列式是“0.5÷0.8”，第二问是“0.8÷0.5”。

综上所述，小学生数学探究性学习障碍形成原因是复杂的，如何寻找对策，扫清障碍，这条探究之路还需且行且“思”。