基于多变量加权一阶局域混沌预测模型优化及应用
张淑清, 刘子玥, 何泓运, 任 爽, 张立国, 姜万录
(燕山大学 电气工程学院, 河北 秦皇岛 066004)
1 引 言
混沌预测的主要思想是根据历史时间序列对未来序列做预测。在重构相空间的基础上,人们先后提出了全域法、局域法、加权一阶局域法等方法[1~3]。全域法计算很复杂,仅适合光滑函数,对于具有较高嵌入维的系统并不适用;局域法具有简单易用、拟合速度快、精度较高等优点,预测效果优于全域法;加权一阶局域法是局域法的优化模型,计算量小,易操作,具有很强的自适应能力和鲁棒性、精度高、通用性强等优点。
然而,这些预测模型仅考虑了单变量时间序列,预测没有考虑其它因素的影响,会造成重要信息的缺失,影响预测精度[4]。鉴于此,本文提出多变量时间序列相空间重构方法,建立多变量加权一阶局域混沌预测模型,并在以下3方面对该模型进行优化:
首先,多变量相空间重构中延迟时间和嵌入维数的选择至关重要。相空间延迟时间的选取方法有自相关函数法、平均位移法、复自相关法、互信息法等;嵌入维数的选取方法有几何不变量法、虚假最邻近点法等;同时确定两个参数的方法有C-C方法和微分熵法等[5,6]。为了简化计算,并且挖掘更多的系统信息,本文基于等概率符号化选取极大联合熵和最小香农熵法分别求最佳延迟时间和嵌入维数。等概率符号化可避免信息遗失,同时提高了符号的利用率[7]。对经典Lorenz混沌系统进行多变量相空间重构,验证了多变量时间序列包含更丰富的系统信息。
其次,采用区间邻近点法确定预测中心点的邻近点,可避免产生伪邻近点,有效减少计算量,同时提高负荷预测模型的准确性。
最后,利用邓氏关联度的概念,分析影响预测的因素,选用关联程度最高的影响因素作为观测变量之一进行预测,从而建立多变量预测模型。
本文对优化的多变量加权一阶局域混沌预测模型进行了数值验证,并应用到电力负荷预测中,在分析影响电力负荷预测的因素和相空间重构的基础上,确定气温作为观测变量之一,建立多变量加权一阶局域混沌预测模型。通过与单变量预测方法比较,验证了本文方法预测精度较高,实用性强。
2 多变量加权一阶局域预测模型
2.1 多变量相空间重构
多变量时间序列的相空间重构方法与单变量时间序列相似[8],对于n维时间序列Xi=(x1,i,x2,i,…,xn,i),i=1,2,…,N,设ti和mi为延迟时间和嵌入维数,则其延迟时间法相空间重构为
Yl=(x1,l,x1,l-t1,…,x1,l-(m1-1)t1,x2,l,x2,l-t2,…,x2,l-(m2-1)t2, …,xn,l,xn,l-tn,…,xn,l-(mn-1)tn)
(1)

2.2 多变量加权一阶局域预测模型
在单变量加权一阶局域预测模型中,设xn为已知量,xn+1为预测量,则包含有这两个分量的最新相空间相点为Xn-(m-1)t=(xn-(m-1)t,xn-(m-2)t,…,xn)和Xn+1-(m-1)t=(xn+1-(m-1)t,xn+1-(m-2)t,…,xn+1)。因此,只要获得相点Xn-(m-1)t的下一轨迹点Xn+1-(m-1)t,并从中分离出唯一未知量xn+1就完成了该值的预测[9]。
由此我们得出,在多变量加权一阶局域预测模型中,设Xi为已知多变量,Xi+1为预测量,按照相空间的演化轨迹,由区间邻近点法得到Xi的邻近点Xir,根据欧式距离计算公式,计算Xi与Xir的距离
(2)
式中:dr为Xir与Xi的距离。设dmin是dr中的最小值,则Xir的权值为
(3)
对Xir和Xir+1进行一阶局域线性拟合,得
Xir+1=ae+bXir
(4)
式中:e为1×m阶矩阵,e=(1,1,…,1)T。
根据加权最小二乘原理,可得
(5)
将式(5)看成是关于a,b的二元函数,两边求偏导,得:
(6)
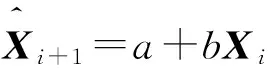
3 多变量混沌预测模型优化
3.1 多变量混沌预测模型子序列重构
针对上述建立的多变量预测模型中的序列Xi的子序列X1,进行基于等概率符号化的极大联合熵[10]和最小香农熵法[11]的相空间重构。
3.1.1 等概率符号化
以多变量时间序列Xi的子序列X1为例,将X1符号化的步骤为:
首先,将序列X1中的元素从小到大排列,得到重排后的序列{xS1,xS2,…,xSn},按公式(7)确定阈值集合{ZC0,ZC1,ZC2,…,ZCd},并将其等概率地分成d个小区间。其中
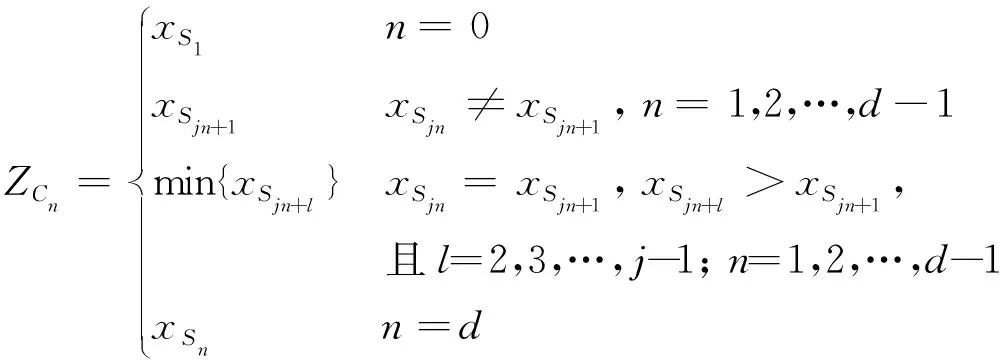
(7)
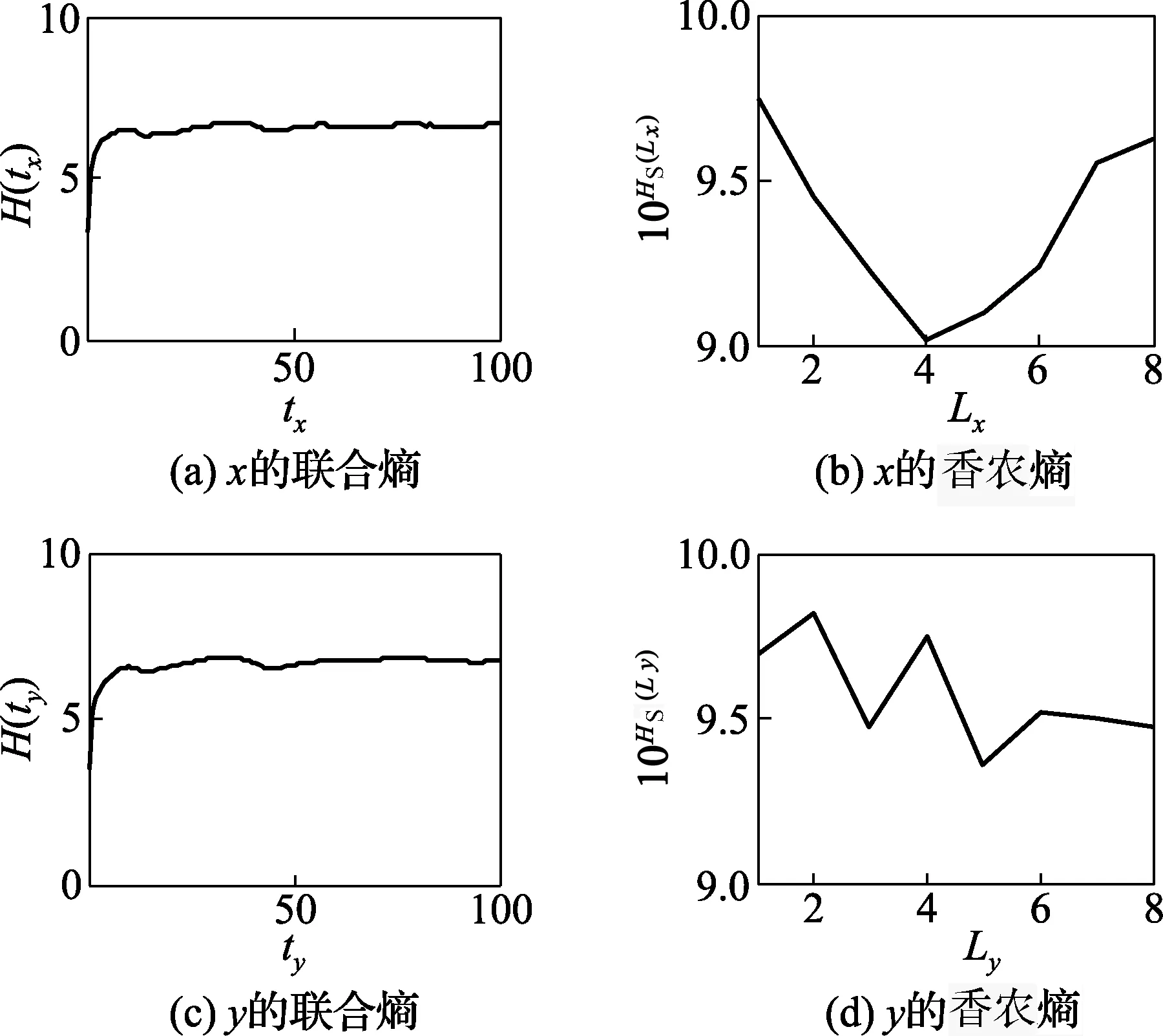
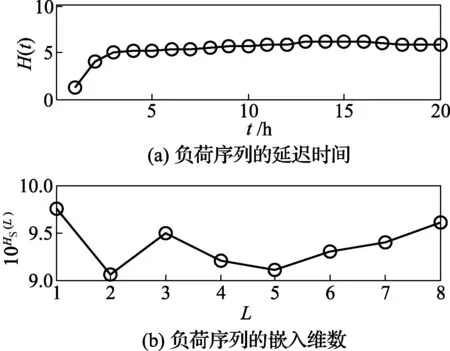
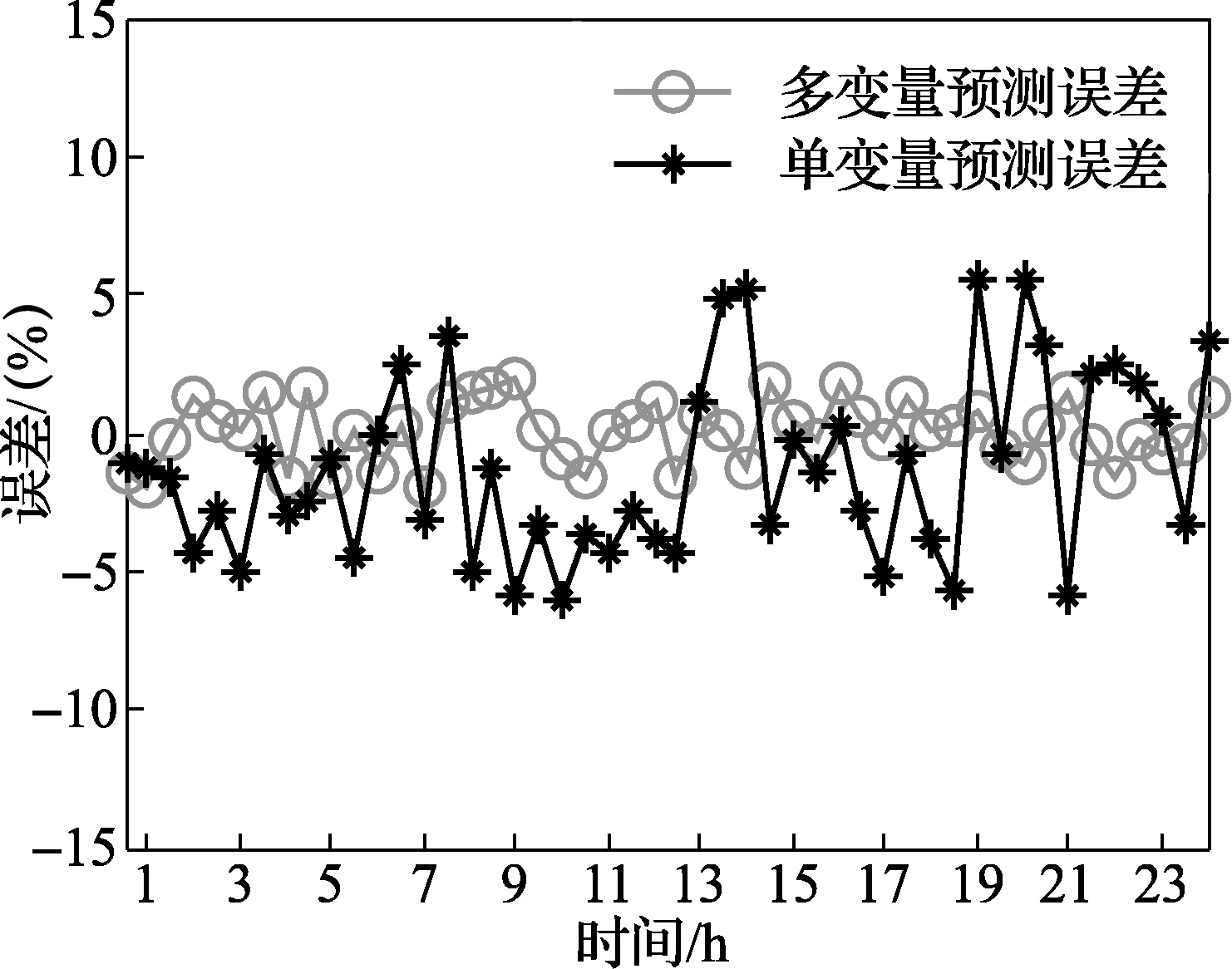
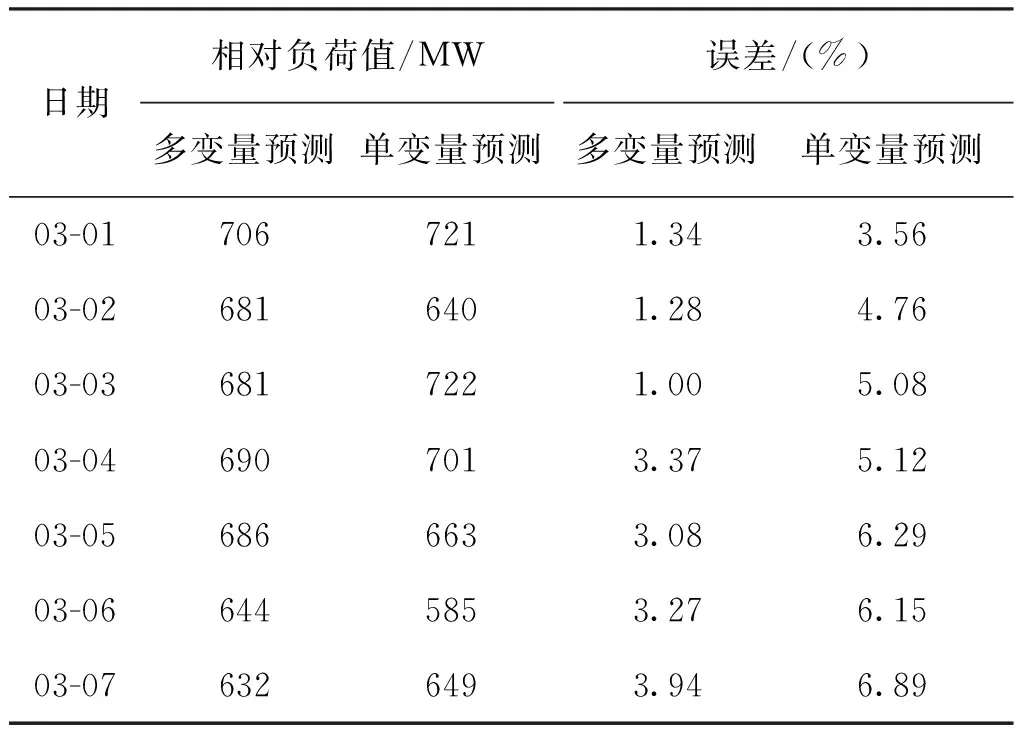
然后,将{xS1,xS2,…,xSn}转换成符号序列组成的符号集Q={n-1|ZCn-1≤xSn 最后,根据文献[10]将其划分成长度为L的短序列,得到新的符号序列[12]。 3.1.2 极大联合熵法求延迟时间 在稳态情况下,对任意的延迟时间t,子序列X1和延迟序列X1,t都具有相同的概率分布和统计特性,则二者的熵值接近于常数,即 H(X1,X1,t) =H(X1)+H(X1,t)-I(X1,X1,t) =C-I(X1,X1,t) (8) 式中:H(X1)为子序列X1的熵;H(X1,t)为延迟序列X1,t的熵;H(X1,X1,t)为联合熵;C为常数;I(X1,X1,t)为互信息函数。 由联合熵与互信息函数的关系式(8),联合熵H(X1,X1,t)的第一极大值点可以确定相空间重构的最佳延迟时间[13]。 等概率符号化将X1和X1,t编码成十进制数序列Lx(n)和Lxt(n),则基于等概率符号分化求取的联合熵公式为 (9) 式中P(Lx,Lxtj)为联合概率。 3.1.3 最小香农熵法求嵌入维数 在等概率符号化的基础上,定义改进的香农熵[14]: (10) 式中:Nseq是符号序列中具有非零概率的符号的总个数;pi,L是第i个长度为L的序列出现的概率。 HS(L)越低意味着原始时间序列中包含确定性的结构。给定符号集大小,香农熵HS(L)的值将随符号序列分割长度L的变化而变化,令L从1开始增加,当HS(L)取最小值时,所对应的L值即为最佳嵌入维数的值[15]。 3.1.4 数值验证 经典Lorenz混沌系统[16]方程为: (11) 由变量x和y构成多变量时间序列,参数σ=16,b=4,r=45.92。对时间序列等概率符号化,得到极大联合熵和最小香农熵如图1所示,可知延迟时间tx=ty=10;嵌入维数mx=Lx=4,my=Ly=5。 图1 Lorenz系统数值仿真实验 图2展示了Lorenz系统在x-y平面的投影,单变量x和单变量y的重构吸引子图以及多变量xy的重构吸引子图。由图可以看出,多变量时间序列在一定程度上比单变量时间序列的重构包含更多的信息,能很好地反映出Lorenz系统的双圈拓扑结构,从而提高预测精度。 图2 重构吸引子图 设多变量时间序列Xi的嵌入维数为mi,延迟时间为ti,序列的最大值为ximax,最小值为ximin,将序列的取值区间[ximin,ximax]均分为h份,定义第v个区间Qv为: Qv=[ximin+(v-1)δi,ximin+vδi] (12) δi=(ximax-ximin)/mi (13) 式中:δi为各个小区间的长度;v=1,2,…,h。 在相空间中,对于给定区间划分数h和中心点Xi=[xn,i,xn-ti,i,…,xn-(d-1)ti,i]T,如果存在某一状态Xir满足式(14),则Xir称为Xi的邻近点[17]。 xn-p-kt,i∈Qv xnr-p-kt,i∈Qv (14) 式中:p=1,2,…;k=0,1,…,mi-1。上述即为区间邻近点的选取方法。 选取中心点x1的邻近点时,若只根据邻近距离ε选,不能排除伪邻近点x3;而区间邻近点思想不仅保证了邻近点位于中心点附近,而且保证了在p个时刻内两点的轨线都很接近,如图3所示,从而避免了伪邻近点的产生[18]。 图3 区间邻近点避免产生伪邻近点的示意图 在进行预测时,不同因素影响程度不同,利用邓氏关联度的概念[19],关联程度最高的影响因素作为观测变量之一进行预测。 (15) (16) 依据某地区2012年1月和2月的负荷及相关数据,对2012-03-01的电力负荷进行预测。首先,对实际电力负荷与相关因素(气温、实时电价和时间)[20,21]做关联分析,所得关联系数曲线如图4所示,其中电力负荷与气温的关联度为0.89,与实时电价的关联度为0.33,与时间的关联度为0.75。由此看出,气温与电力负荷的关联度最高,故选择气温作为负荷预测的观测变量。 图4 电力负荷与各因素的关联系数曲线 然后,采用等概率符号化、极大联合熵和最小香农熵法对电力负荷序列和气温时间序列进行相空间重构,见图5和图6。由图可知,负荷时间序列的延迟时间t1=21,嵌入维数m1=2;气温时间序列的延迟时间t2=4,嵌入维数m2=3。 图5 重构负荷时间序列 图6 重构气温时间序列 最后,在关联分析和相空间重构的基础上,采用本文提出的多变量加权一阶局域混沌预测模型对2012-03-01全天的负荷值进行预测,并与单变量加权一阶局域预测模型的预测结果进行比较,见图7、图8和表1。 图7 多变量与单变量预测负荷比较 图8 多变量与单变量预测误差比较 表12012-03-01负荷预测的平均误差与平均计算时间 参数多变量预测单变量预测平均误差/(%)平均计算时间/s0.8130.6342.9670.425 由图7、图8和表1可见,多变量预测模型在计算时间上与单变量预测模型相差不大,但在预测精度上具有明显优势。因此,多变量预测模型可以在保证计算时间的同时提高模型的预测精度。 为了进一步验证多变量预测方法的有效性,对2012-03-01到2012-03-07一周的电力负荷进行预测,并对一周的日最高负荷预测结果进行误差分析,结果见表2。 表2 一周负荷预测误差分析 由表2可以看出,多变量局域区间预测方法对一周的负荷预测的结果优于单变量预测方法。因此,验证了多变量预测方法应用到电力负荷预测的有效性。 在多变量相空间重构思想的基础上,建立多变量加权一阶局域混沌预测模型。采用基于等概率符号化的极大联合熵和最小香农熵法进行相空间重构,能够有效挖掘时间序列的信息,并用经典的Lorenz混沌模型验证了该重构方法的有效性。优化的多变量混沌预测模型应用于短期电力负荷预测,利用相关分析得到气温是与负荷相关程度最高的影响因素,将电力负荷和气温序列结合起来,相较于单变量负荷时间序列预测方法,明显提高了负荷的预测精度。 [参考文献] [1] 肖白,周潮,穆钢.空间电力负荷预测方法综述与展望[J].中国电机工程学报,2013,33(25):78-92. [2] Hu Y, Chang X. Short-term load forecasting based on local wave method and LSSVM[J].ElectricalMeasurement&Instrumentation, 2015, 52(7):5-9. [3] 王书涛,李梅梅,张淑清,等.基于多重分形去趋势波动的机械故障诊断新方法[J].计量学报,2012,33(3):232-235. [4] 郭创新,王扬,沈勇,等.风电场短期风速的多变量局域预测法[J].中国电机工程学报,2012,32(1):24-31. [5] 马哲,舒勤.基于ESPRIT分解算法的短期电力负荷预测[J].电力系统保护与控制,2015,43(7):90-96. [6] 张淑清,师荣艳,董玉兰,等.双变量小波阈值去噪和改进混沌预测模型在短期电力负荷预测中的应用[J].中国电机工程学报,2015, 35(22):5723-5730. [7] 张淑清,董璇,翟欣沛,等.基于EEMD和混沌的信号特征提取方法及应用[J].计量学报,2013,34(2):173-179. [8] 张淑清,任爽,师荣艳,等.基于多变量气象因子的LMBP电力日负荷预测[J].仪器仪表学报,2015,36(7):1646-1652. [9] 王玉田,李长吾,李艳春,等.基于小波神经网络的农药荧光光谱识别[J].计量学报,2008,29(1):84-86. [10] 张淑清,李新新,张立国,等.基于符号分析的极大联合熵延迟时间求取方法[J].物理学报,2013,62(11):110506-110511. [11] 张雨.时间序列的混沌和符号分析及实践[M].长沙:国防科技大学出版社,2007. [12] 黄晓林,霍铖宇,司峻峰,等.等概率符号化样本熵应用于脑电分析[J].物理学报,2014,63 (10):26-31. [13] 张淑清,李盼,冯璐,等.基于LMD能量熵和GK模糊聚类的电能质量扰动识别[J].计量学报,2016,37(1):90-95. [14] Chaturvedi D K, Sinha A P, Malik O P. Short term load forecast using fuzzy logic and wavelet transform integrated generalized neural network[J].InternationalJournalofElectricalPower&EnergySystems, 2015, 67:230-237. [15] 刘明.基于连云港市的电力系统短期负荷预测研究[J]. 东北电力技术, 2015,36 (2):29-34. [16] 张素香,赵丙镇,王风雨,等.海量数据下的电力负荷短期预测[J].中国电机工程学报, 2015,35(1):37-42. [17] 刘自发,庞铖铖,王泽黎,等.基于云理论和元胞自动机理论的城市配电网空间负荷预测[J].中国电机工程学报,2013,33(10):98-105. [18] 管红立,王博文,赵智忠.基于相空间重构和Lyapunov 指数电弧电压混沌特性分析[J]. 燕山大学学报, 2017,41(2):149-155. [19] 于之虹, 黄彦浩, 鲁广明,等.基于时间序列关联分析的稳定运行规则提取方法[J]. 中国电机工程学报, 2015 35(3):519-526. [20] 张淑清,任爽,姜安琦,等.PCA-GRNN在综合气象短期负荷预测中的应用[J].计量学报, 2017, 38(3): 340-344. [21] 孙冠群,张黎锁.基于细菌觅食算法的异步电动机现场效率估算[J].计量学报,2017,38(2):215-219.

3.2 邻近点的确定

3.3 关联分析确定观测变量

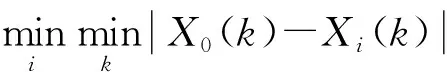
4 实际电力负荷预测




5 结 论

