基于相关主成分分析和极限学习机的 风电机组主轴承状态监测研究

何 群, 王 红, 江国乾, 谢 平, 李继猛, 王腾超

(燕山大学 电气工程学院 河北省测试计量技术及仪器重点实验室, 河北 秦皇岛 066004)

1 引 言

风能作为一种潜力巨大的可再生能源受到了广泛的关注,全球风电装机容量呈现逐年上涨的趋势。然而,伴随着装机容量的不断增加,机组的故障率也在不断增加,导致高额的维护费用和停机损失严重影响了风场的经济效益。因此,风电机组运行状态监测已成为风电产业需要迫切解决的问题之一。目前,常用的状态监测方法包括振动、油液和数据采集与监视控制系统(supervisory control and data acquisition, SCADA)监测等,但是振动和油液监测方法测试系统复杂、成本较高;而SCADA系统监测数据获取较容易,并可实时对机组及其主要部件的运行状况进行记录、存储,其已成为近年来风电状态监测的研究热点[1]。

文献[2]基于风电机组SCADA运行数据建立正常工作行为模型,有效地实现齿轮箱、发电机异常及故障的检测；文献[3]运用聚类技术挖掘SCADA系统监测参数间的关系,实现了早期故障的自动检测；一些学者也分别针对发电机[4]、齿轮箱[5～7]和塔架[8]的故障检测开展了类似的研究工作。然而,针对主轴承展开的研究则较少。

近年来,神经网络在SCADA数据建模和状态监测方面得到了广泛的应用,如误差反向传播(error back propagation, BP)网络,然而其存在学习过程收敛速度慢、容易陷入局部极小点、鲁棒性不好以及网络性能差等缺点[9]。基于此,文献[10]提出了一种新型学习算法——极限学习机(extreme learning machine, ELM)。该方法学习速度快、泛化能力强,已成功应用于软测量建模[11～13]及短期负荷预测[14]等领域。因此，将此方法作为本文的主要建模方法。首先对某机组的SCADA数据进行预处理,建立主轴承正常运行时的温度模型并用其进行温度预测;其次采用滑动窗和核密度估计方法对正常运行时的残差进行分析,确定主轴承异常监测时所需的阈值。当模型预测的温度残差分布特性超出设定的阈值时,发出报警。本文从整体上实现了主轴承潜在故障的预测。

2 风电机组SCADA监测参数

本文所用数据为内蒙古某风电场1.5 MW变速恒频风力发电机组的监测数据。该风电机组的SCADA系统每隔30 s采集并记录一次机组的参数,记录的内容包括主轴承温度、风速和环境温度等共47个连续量参数,同时还包括机组的运行状态、子系统或部件的启动次数、运行时间等共25个离散量信息。该离散量信息同时设定了各个子系统或部件各个监测量的“安全阈值”,一旦所采集的数据超出此阈值,系统就会报警。但此阈值设定范围较广,往往达到该阈值时,风机已经发展到“故障停机”的地步。本文从SCADA连续量监测数据入手,充分利用主轴承与其他子系统或部件之间的相互作用关系,实现主轴承的异常状态监测。

3 主轴承温度ELM建模

3.1 ELM原理

(1)

式中:j=1,2,…,N;wi=[wi1,wi2,…win]T为网络输入层到隐含层的连接权值;βi=[βi1,βi2,…,βim]T为隐含层节点到输出层的连接权值;bi为第i个隐含层神经元的阈值;g(x)为激活函数;wi·xj为wi和xj的内积。

单隐含层神经网络学习的目的是使输出的误差最小,即存在βi、wi和bi,使得

(2)

式(2)可以简化为:

Hβ=T

(3)

式中:H称为神经网络的隐含层输出矩阵;T为网络输出矩阵。

(4)

式中H+为隐含层输出H矩阵的广义摩尔逆。

3.2 主轴承ELM建模变量选取

为建立主轴承ELM模型,选取表征主轴承运行状态的主轴承温度作为模型的输出变量。同时采用相关-主成分分析法(principal component analysis, PCA)选取与主轴承温度密切相关的变量作为模型的输入变量。所用数据为该机组2014年7月29日至8月4日正常运行的SCADA数据。首先采用相关系数法来确定模型的初始输入变量。计算主轴承温度与其它46个变量两两之间的相关系数。在计算之前,为了减少数据随机性和各变量之间量纲不同对计算结果产生的影响,对数据进行平滑和归一化处理,归一化到[-1,1]之间。本文选用相关系数的绝对值大于0.6的变量作为模型初始输入变量,选择结果见表1。

表1 主轴承温度与初始输入变量的相关系数

为了消除以上9个初始输入变量之间的相关性和冗余性,采用主成分分析方法[15]来提取主成分作为模型新的输入,从而减少模型训练的复杂性以及提高模型的预测精度。各个主成分所对应的特征值、方差贡献率以及累计方差贡献率如表2所示。一般地,当累计贡献率大于85%时,就认为新变量能足够反映原变量的信息。由表2可见,当包含5个主成分时,累计贡献率达到98%以上,表明新变量涵盖了原始变量多于98%的信息。进一步验证表明,含有5个主成分时的预测精度最高,因此将原来的9个变量转化为线性无关的5个变量作为ELM模型的输入。并可按照图1对新的输入数据进行分析。

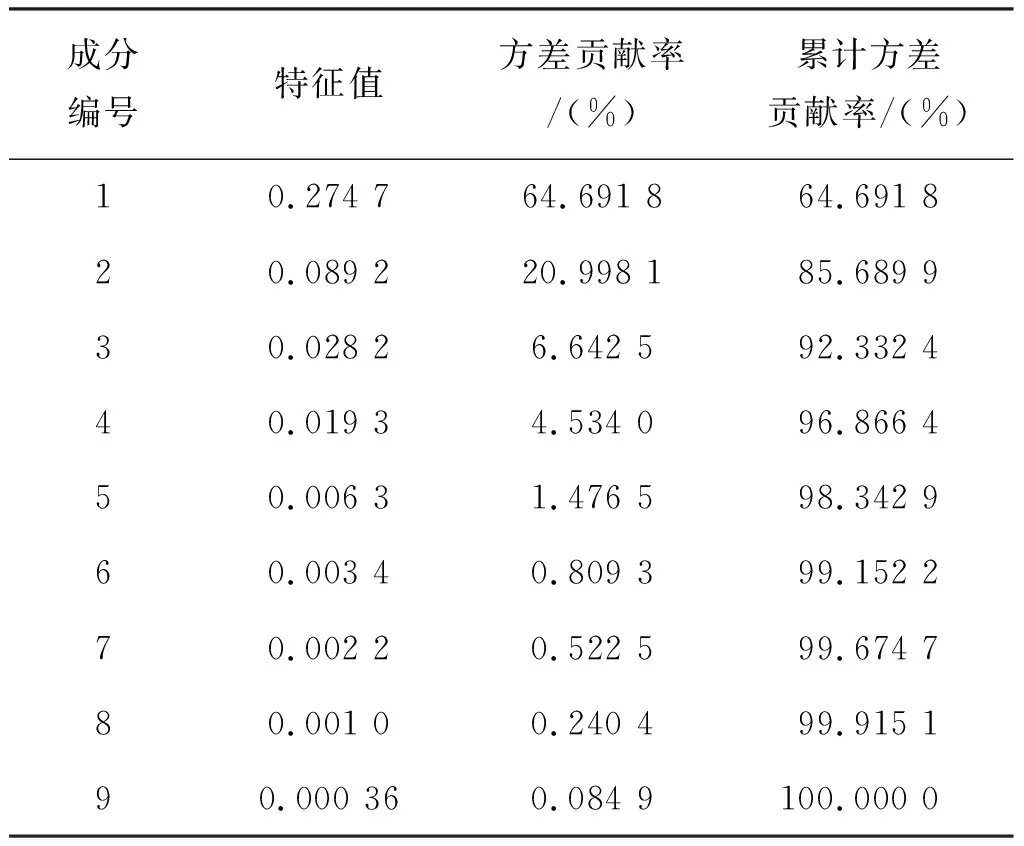
表2 方差及主成分贡献率

图1 研究路线框图

4 基于ELM的主轴承温度预测

4.1 主轴承ELM温度模型有效性验证

为了使ELM模型能够覆盖主轴承的正常工作空间以及尽可能包含正常时的全部工况,选取3.2节所提的2014年7月29日至8月4日机组正常运行、功率大于零的14 318个历史SCADA样本作为模型的训练样本集,8月22日正常运行的2 873个样本作为测试样本集。采用本文所提方法与相关ELM以及相关BP方法进行预测,并选择合理的隐含层节点个数,预测结果如图2和图3所示。

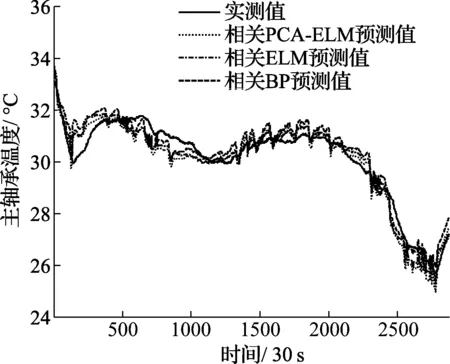
图2 正常情况下主轴承温度实际值与预测值对比图

图3 正常情况下主轴承温度预测残差对比图

为了能够定量地对图2和图3的预测结果进行分析,分别以3种方法的训练时间、均方根误差(RMSE)、平均绝对误差(MAE)和平均百分比误差(MAPE)作为性能评价指标,结果见表3所示。

表3 3种预测方法对比

图2、图3以及表3数据分别为模型试验100次的平均值。由表3可知:主轴承在正常运行状态下,相关ELM方法无论是从训练时间还是预测精度方面都优于相关BP;同时,相关PCA-ELM由于输入变量只有5个,结构简单,所用训练时间最少,且预测精度高于相关ELM。

4.2 主轴承预测残差分析

为实时反映主轴承温度残差特性的变化,以及消除随机因素的干扰,使用图4所示的滑动平均窗口方法对残差进行滑动平均处理,其中N为滑动窗口的宽度;同时,为根据残差的特性变化检测主轴承的异常变化,采用式(5)所示的核密度估计方法来设定检测阈值。

(5)

式中:n为样本总数;xi为给定样本;h为带宽或平滑参数;K为核函数,并且满足下式:

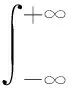
(6)

图4 残差滑动窗口工作原理

滑动窗口的宽度N取为120,核函数采用高斯核函数,置信度取为0.99。对4.1节中验证集中主轴承正常运行时3种方法的残差序列分别进行分析,确定主轴承异常监测时各种方法所需的阈值。当模型预测的主轴承温度残差滑动窗口统计特性超过预先设定的阈值时,发出报警。

在该风电机组的SCADA数据中,没有主轴承从正常运行到出现故障的记录。为了验证本文所提基于相关PCA-ELM方法监测主轴承故障的有效性,基于实测的SCADA数据进行故障模拟,模拟主轴承故障时导致主轴承温度升高的情况。对验证集中于8月22日的2 873个历史数据从第1 001点开始对主轴承温度变量加入步距为0.005的累计温度偏移,以达到主轴承故障从发生到故障程度不断加深的过程。故障预测结果如图5所示。

图5 主轴承故障预测结果

同时,分别使用相关BP和相关ELM方法进行故障预测。3种方法的残差滑动窗口特性以及报警阈值如图6所示。

图6 主轴承故障预测残差滑窗特性和报警阈值

由图6可以看出,使用相关BP、相关ELM和相关PCA-ELM进行故障预测时,经过滑动平均处理后的残差曲线分别在第1 069、937、726个滑动窗口超出预先设定的报警阈值,且随着故障程度的加深,超出报警阈值的程度也在不断增大。考虑到滑动窗口的宽度N为120,可以得出3种方法分别在第1 189、1 057、846点检测出了主轴承的异常变化。比较发现,相比于相关BP和相关ELM方法,本文所提的基于相关PCA-ELM状态监测方法可以有效地实现主轴承潜在故障的预测。

5 结 论

在风电机组实测SCADA数据的基础上,运用相关分析法与主成分分析法对SCADA数据进行处理,建立主轴承正常运行时的ELM温度模型并用其进行温度预测,并运用滑动窗口统计方法与核密度估计方法来确定主轴承工作异常监测阈值,实现故障早期检测。对比结果表明:本文所提的基于相关PCA-ELM方法具有更快的学习速度以及更高的预测精度,同时能够更早预测故障的发生。该方法可进一步用于机组其他部件监测变量的建模分析和故障预测。

[参考文献]

[1] 赵文爽. 风机异常状态监测与关键参数预测方法研究[D]. 秦皇岛:燕山大学, 2015.

[2] Zaher A, McArthur S D J, Infield D G,etal. Online wind turbine fault detection through automated SCADA data analysis[J].WindEnergy, 2009, 12(6):574-593

[3] Kim K, Parthasarathy G, Uluyol O,etal. Use of SCADA data for failure detection in wind turbines[C]//Presented at the 2011 Energy Sustainability Conference and Fuel,Cell Conference.Washington D C, USA, 2011.

[4] Guo P, Infield D, Yang X. Wind turbine generator condition-monitoring using temperature trend analysis[J].IEEETransactionsonSustainableEnergy, 2012, 3(1): 124-133.

[5] 郭鹏, David Infield, 杨锡运. 风电机组齿轮箱温度趋势状态监测及分析方法[J]. 中国电机工程学报, 2011, 31(32): 129-136.

[6] 顾煜炯, 宋磊, 徐天金, 等. 变工况条件下的风电机组齿轮箱故障预警方法[J]. 中国机械工程, 2014, 25(10) :1346-1351.

[7] 董玉亮, 李亚琼, 曹海斌, 等. 基于运行工况辨识的风电机组健康状态实时评价方法[J]. 中国电机工程学报, 2013, 33(11): 123-127.

[8] 郭鹏, 徐明, 白楠, 等. 基于SCADA运行数据的风电机组塔架振动建模与监测[J]. 中国电机工程学报, 2013, 33(5): 128-135.

[9] 龙泉, 刘永前, 杨勇平. 基于粒子群优化BP神经网络的风电机组齿轮箱故障诊断方法[J]. 太阳能学报, 2012, 33(1):120-125.

[10] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine : theory and applications[J].Neurocomputing,2006, 70(1-3): 489-501.

[11] 潘孝礼, 肖冬,常玉清,等. 基于极限学习机的软测量建模方法研究[J]. 计量学报,2009, 30(4) : 324-327.

[12] 毛志忠, 唐奡, 肖冬. 基于 ELM 的非线性 PLS 软测量方法研究[J]. 计量学报, 2010, 31(4): 374-378.

[13] 谢平,王一凡,江国乾,等. 基于样本熵的风力发电机早期故障检测[J]. 计量学报, 2017,38(5): 626-630.

[14] 成天乐, 周胜瑜, 李斯, 等. 基于极限学习机方法的短期负荷预测[J]. 电力科学与工程, 2013, 29(4): 24-29.

[15] 周松林, 茆美琴, 苏建徽. 基于主成分分析与人工神经网络的风电功率预测[J]. 电网技术, 2011, 35( 9) : 128-132.