大空间坐标测量网络的现场实时标定方法
张红英, 余晓芬, 王 标
(合肥工业大学 仪器科学与光电工程学院, 安徽 合肥 230009)
1 引 言
大空间坐标测量网络是一种分布式大尺寸测量设备,主要由若干测量基站组成,仅依靠距离信息即可根据多边法原理计算出距离交会点的空间坐标[1~4]。由于对测量基站的旋转精度及定位精度要求不高,且采用了相对成熟的激光脉冲绝对测距技术,单个测量基站的构建成本较低。另外,精度自适应的构建方法[5]还最大限度地优化了网络布局,减少了构建网络所需测量基站的数量,间接提高了网络的测量速度。上述因素使得网络的测量成本大大低于现有大尺寸测量设备,如室内GPS、激光跟踪仪等[6,7]。按精度自适应方法所得布局现场构建测量网络后,需首先标定出各个测量基站的空间坐标才能对工件待测点进行测量。另外,大尺寸测量的任务周期一般较长,干扰因素较多,需在测量过程中实时重新标定测量基站的坐标,以及时修正测量误差。因此,大空间坐标测量网络的现场、实时标定方法是网络构建的关键。
现有测距多边法坐标测量系统的标定方法主要有基于动点冗余测量和基于基站间距测量两种。前者要求系统包含N(N≥4)个跟踪测距基站(如文献[8]所叙述的系统)或在N个站位上依次进行测量(如文献[9]所叙述的系统),其标定原理是每增加一个被测动点都会引入3个未知量,同时得到N个距离约束方程,当被测动点足够多时方程个数将超过未知量个数,超定方程组的最小二乘解即包含基站坐标信息[10]。具体计算时,若直接规定坐标系原点及方向,最小二乘解则被转化为无约束的最优化问题[11,12];若通过约束条件间接规定坐标系原点及方向,最小二乘解则被转化为有约束的最优化问题[13]。基于动点冗余测量的标定方法仅依靠基站自身的测距功能即可完成系统标定,不增加系统的测量成本,但其标定效果受系统布局、动点布局等多种因素的影响,存在较大的不确定性,且模型解算较为复杂,难以实现实时标定,见文献[2]。后者是根据基站间的距离信息建立相应的约束方程组,进而计算出基站坐标。该标定模型解算简单,同样可仅利用基站的测距功能完成系统标定,但其仅适用于基站非共面布局[14]的测量网络,具有很大局限性,且需对测距瞄准方法进行研究以获取标定所需距离信息。
本文结合上述两种标定方法,提出了模拟基站的标定模型,并研究了相应的测距瞄准方法,解决了大空间坐标测量网络的现场、实时标定问题。
2 多边法原理及测量基站结构
2.1 多边法原理
设空间中有n个坐标已知点(xi,yi,zi)(i=1,2,…,n,n≥3),所求被测点坐标为(x,y,z),第i个坐标已知点和被测点之间的距离为di,则可建立如下距离约束方程组:
(1)
获取距离di后,即可计算出被测点坐标,坐标测量精度σ为:
σ=(trace[(ATA)-1])1/2·σ0
(2)
式中:σ0为距离测量精度;A为距离对被测点坐标偏导数的雅克比矩阵,推导过程见文献[5]。
2.2 测量基站的结构
测量基站主要由激光测距传感器(laser distance measuring sensor,LDMS )、水平旋转机构、竖直旋转机构及标靶板组成[15],结构如图1所示。水平旋转机构和竖直旋转机构的转轴及LDMS的测距光轴正交于一点,称该点为测量基站的旋转中心;标靶板安装在LDMS的背面,且标靶板中心在LDMS的测距光轴上,结构见图2。LDMS的测距起始端面与旋转中心之间的距离为c1,标靶板中心与旋转中心之间的距离为c2,两者均为常数。测量基站的旋转机构工作时,旋转中心的空间位置保持不变。因此可标定出旋转中心的坐标,并将旋转中心作为距离约束方程组(1)中的坐标已知点。
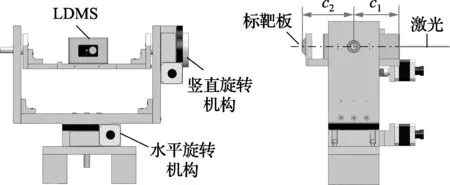
图1 测量基站结构图

图2 标靶板
3 网络的标定方法
因LDMS测距时需与被测点之间保持通视,故通常将大空间坐标测量网络的布置区域设定在待测空间上方或两侧。这种条件下,在精度自适应方法所得布局中,测量基站多处于共面或近似共面状态,因此,测量网络标定方法的研究主要在共面布局的条件下进行。
3.1 模拟基站标定模型
模拟基站标定方法是指:在远离测量基站安装面的位置上设置球形标靶,并以标靶球心模拟测量基站的旋转中心,进而完成测量网络的标定。如图3所示,假设精度自适应方法所得布局中含有4个测量基站,编号分别为Mi,i=1,2,3,4;布置的模拟基站记为B。
建立测量坐标系O-xyz:以M1的旋转中心为坐标原点,将M2的旋转中心设在x轴正方向上,M3的旋转中心设在xOy面上。设Mi旋转中心坐标为(xMi,yMi,zMi),B的中心点坐标为(xB,yB,zB); 另设
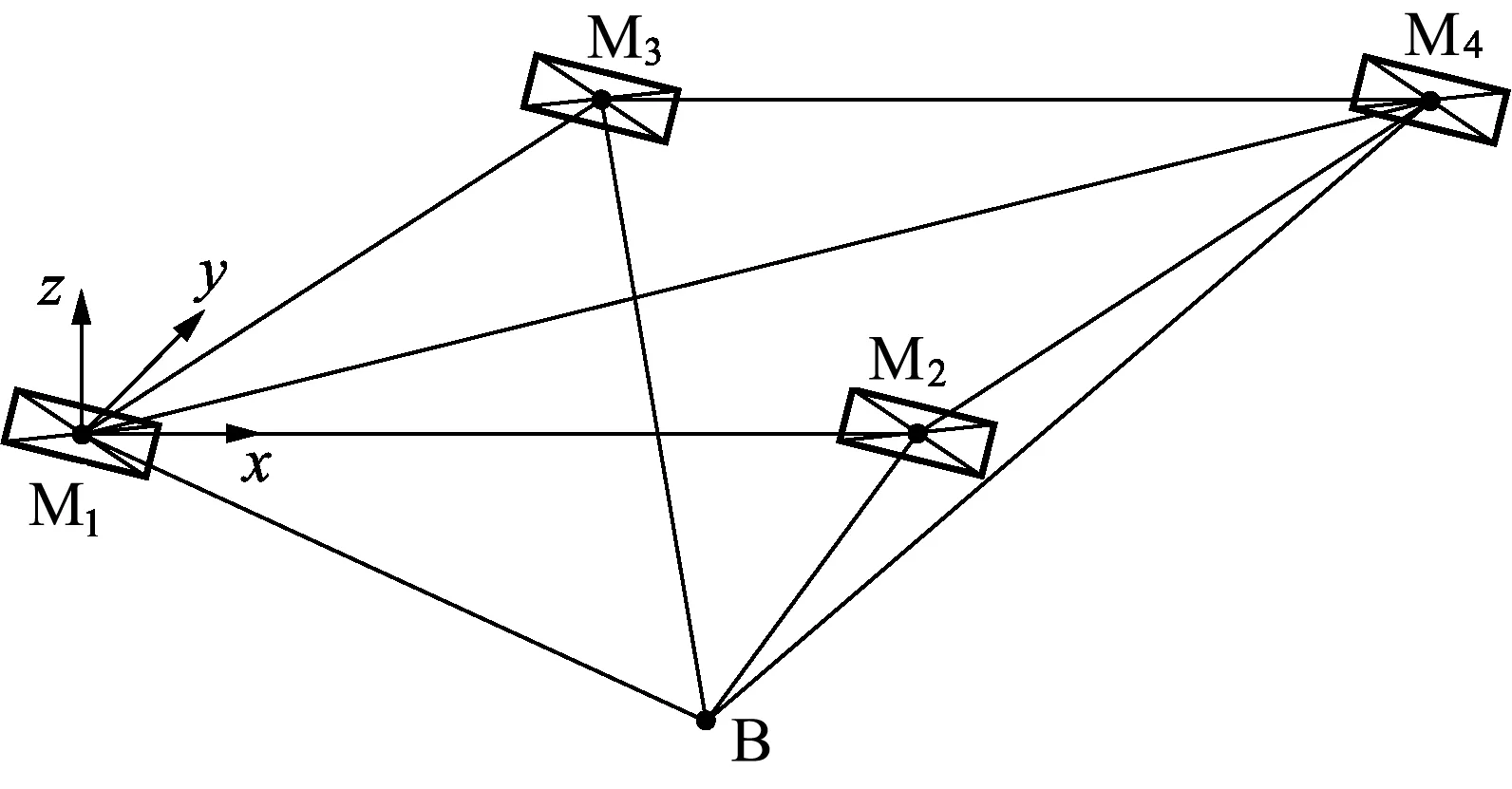
图3 模拟基站标定示意图
Mi和Mj旋转中心间距离为dij,Mi的旋转中心与B的中心点间的距离为diB,则模拟基站标定模型为:
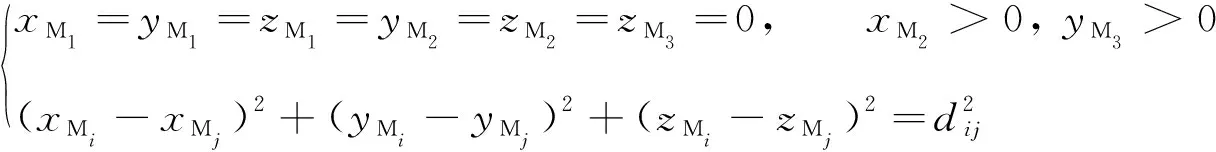
(3)
(4)
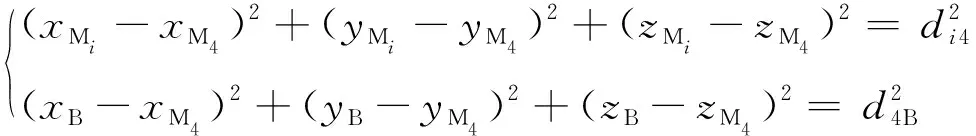
(5)
式中:i=1,2,3;j=2,3,且j>i。
可以发现,标定模型由3组方程组成:当布局中只含有3个测量基站时,无需设置模拟基站,按式(3)建立标定方程即可;当测量基站的数量超过3个时,需先按式(3)标定出部分测量基站旋转中心的坐标,然后按式(4)标定出模拟基站中心点的坐标,最后按式(5)标定出其余测量基站旋转中心的坐标。
显然,模拟基站的安装位置及标定精度对测量基站最终的标定效果均有影响。为此采用搜索精度最佳点的方式确定其安装位置:首先以Mi(i=1,2,3)的旋转中心为坐标已知点,以B的中心点为被测点,根据公式(2),将B的中心点坐标设为自变量,搜索出网络的最佳测量精度及此时模拟基站的位置(xP1,yP1,zP1);然后以Mi(i=1,2,3)的旋转中心和B的中心点为坐标已知点,以M4的旋转中心为被测点,根据公式(2),同样将B的中心点坐标设为自变量,搜索出网络的最佳测量精度及此时球心的位置(xP2,yP2,zP2);最后取P1和P2连线的中点为球形标靶的安装位置。搜索过程中,测量基站的坐标由精度自适应方法根据待测点的理论坐标及要求的测量精度给出。搜索精度最佳点的方法,综合考虑了模拟基站的标定精度及用其标定M4时的网络测量精度。
3.2 测距瞄准方法
模拟基站标定模型涉及两类距离信息:①测量基站旋转中心之间的距离;②测量基站旋转中心和模拟基站中心点之间的距离。快速、准确地获取上述距离是实现测量网络现场、实时标定的关键。
3.2.1 主动扫描瞄准
如图4所示,为确定测量基站M1和M2旋转中心之间的距离,使M1瞄准M2的标靶板中心。
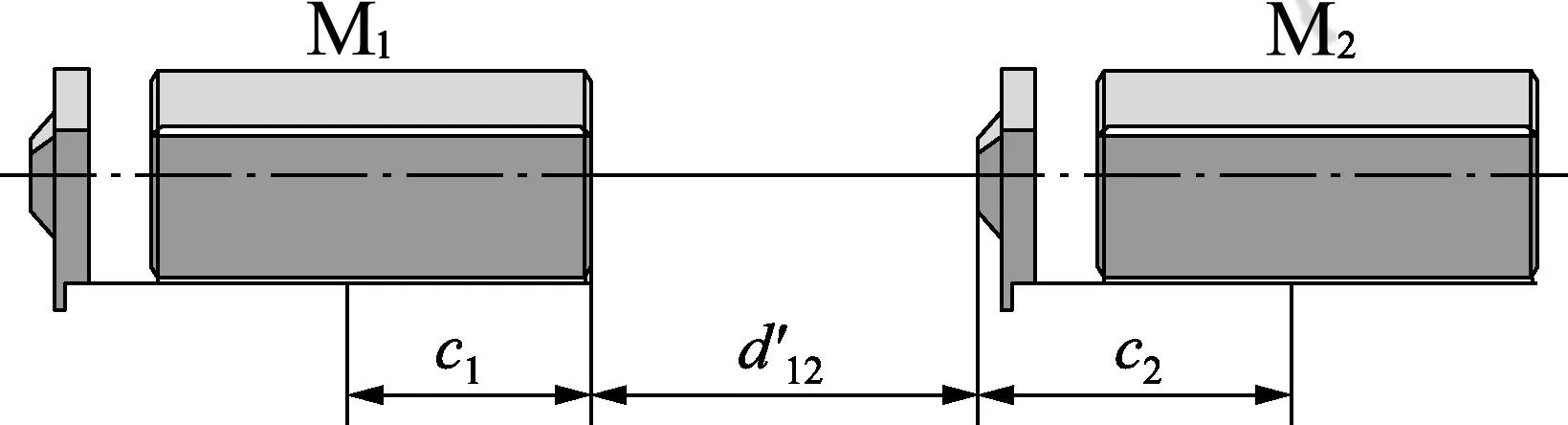
图4 获取第一类距离信息原理图
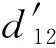
(6)
称实施瞄准测距的测量基站为主动基站,如图4中M1;称被瞄准测距的测量基站为被动基站,如图4中M2。显然,获取第一类距离信息的关键是使主动基站和被动基站的激光光轴共线。
主动扫描瞄准是指,使主动基站对被动基站的标靶板在两维旋转方向上分别进行测距扫描,并根据扫描结果调整两测量基站的瞄准角度。以调整测量基站水平旋转维度上的瞄准角为例,图5是主动基站对被动基站标靶板在水平旋转方向上的测距扫描曲线。X轴数值是测距序号,Y轴数值是距离值;扫描的法向步距为Δd;A是扫描起点,位于标靶板的左侧边缘,扫描次序记为nA;F是扫描终点,位于标靶板的右侧边缘,扫描次序记为nF;C和D对应标靶板中心凸起区域的边界点,对应的距离值分别记为dC和dD,扫描次序分别记为nC和nD。则被动基站的被瞄准角度调整值:
(7)
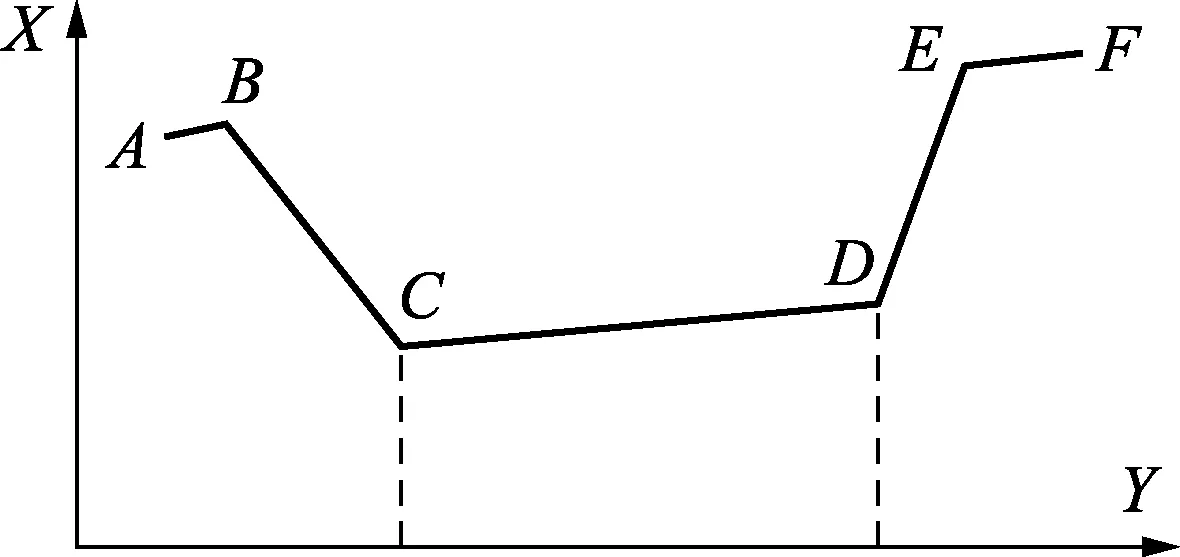
图5 标靶板测距扫描曲线
主动基站的瞄准角度调整值:
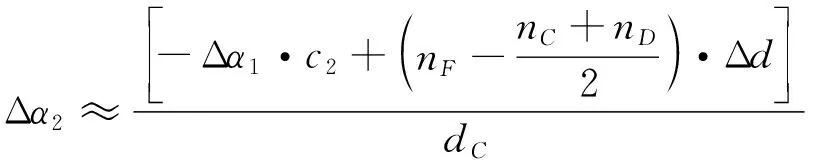
(8)
式(7)和式(8)均以测量基站逆时针旋转为角度增加方向。使两测量基站在水平旋转方向上分别按所得调整值转动,即可完成水平旋转维度上的共线调整。同理,完成竖直旋转维度上的瞄准角调整后即可使主动基站和被动基站的激光光轴共线。
3.2.2 寻心扫描瞄准
寻心扫描瞄准用于获取第二类距离信息。如图6所示,对模拟基站进行测距时需使测量基站的激光光轴瞄准球心,并按式(9)修正测距值d′。
d=d′+c1+r
(9)
式中:r是模拟基站的半径。

图6 获取第二类距离信息原理图
寻心扫描瞄准过程如下:首先保持测量基站的竖直转角不变,使测量基站在水平旋转维度上对标靶进行测距扫描,并使测量基站回转到测距值最小点处;然后保持测量基站的水平转角不变,使测量基站在竖直旋转维度上对标靶进行测距扫描,同样使测量基站回转到测距值最小点处,从而使测量基站的激光光轴瞄准模拟基站的中心点。
4 实验验证
4.1 仿真实验
为验证所提标定模型的效果,进行了仿真实验,分别对“未使用模拟基站”、“在普通位置上安装模拟基站”、“在精度最佳点上安装模拟基站”3种条件下测量网络的标定效果进行了比对。限于篇幅,仅以其中一组仿真为例说明实验结果:测量基站M1、M2、M3和M4的安装坐标分别被设定为(0,0,0)、(5 000,0,0)、(500,5 000,0)和(4 500,4 500,-500),mm;测量基站的测距误差分布为N(0,0.52),设定的普通位置为(300,350,-3000),搜索得到的精度最佳点为(2300,2350,-2 950)。标定实验重复进行50次,3种条件下测量基站M4的坐标标定误差(按方和根公式计算)如图7所示。
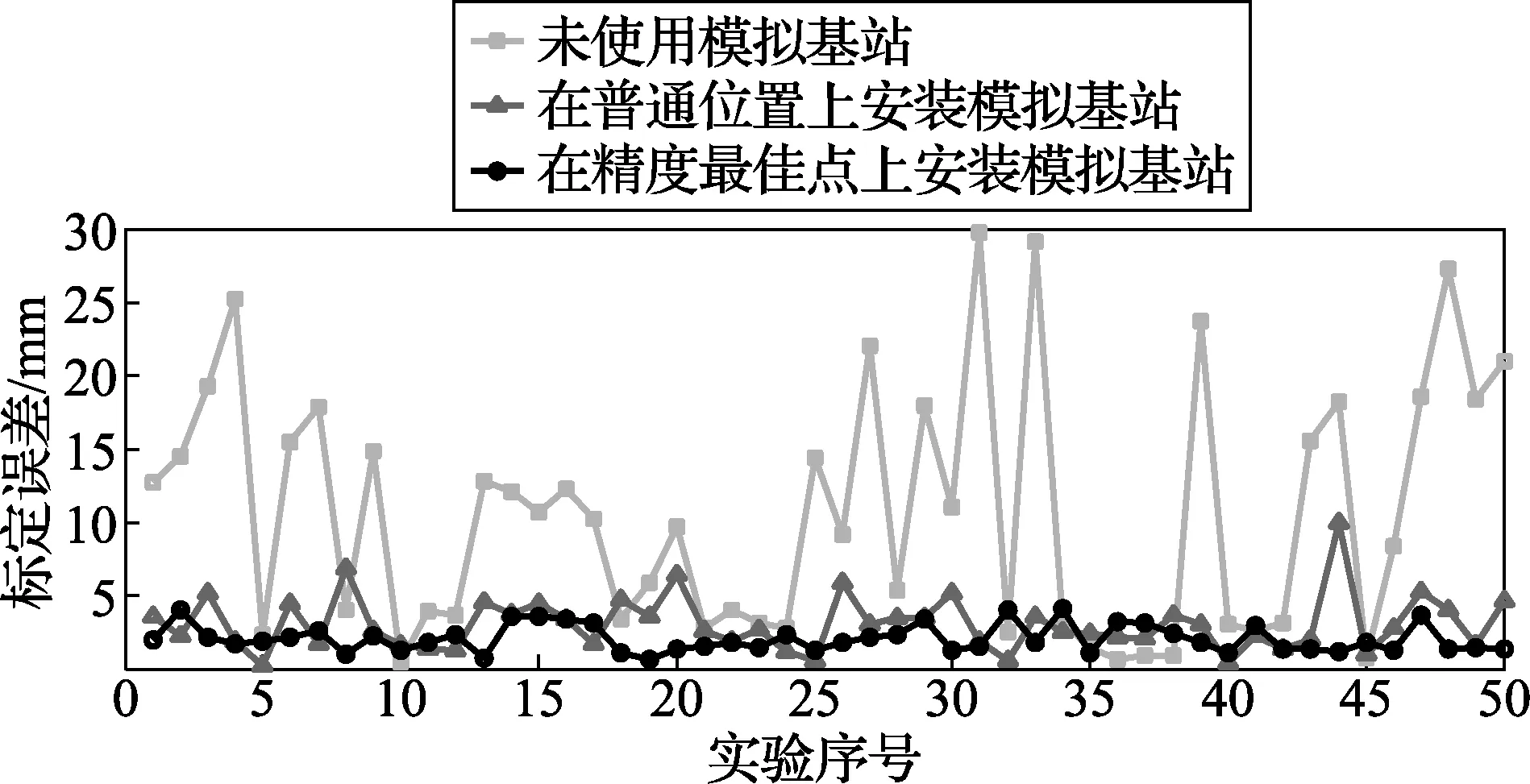
图7 测量基站标定误差曲线图
从图7可以看出,直接使用M1、M2和M3标定M4时,标定误差很大,误差均值约为10.7 mm;在普通位置上安装模拟基站时,标定误差均值约为3.1 mm;在精度最佳点安装模拟基站标定模型时,标定误差均值约为2.1 mm。后两者较为接近,但在精度最佳点安装模拟基站的标定效果更好。这说明,所提标定模型能够很好地完成共面布局下的测量网络标定,且可根据现场情况适当调整模拟基站的安装位置。
4.2 瞄准实验
为验证所提测距瞄准方法的效果,分别编制了相应的测距扫描程序并进行了测试。实验以测量基站重复瞄准后测距值的标准差作为瞄准效果的评判依据。所用测量基站的测距分辨率为0.1 mm,标称的测距标准差为0.5 mm,测量基站照片见图8,模拟基站的直径为52.5 mm。实验结果见表1表2。

图8 测量基站
上述实验结果中,主动扫描瞄准所得测距值标准差最大值为0.16 mm,寻心扫描瞄准所得测距值标准差最大值为0.34 mm,均与测量基站标称的测距标准差在同一数量级上。这表明两种瞄准方法均是可行的。
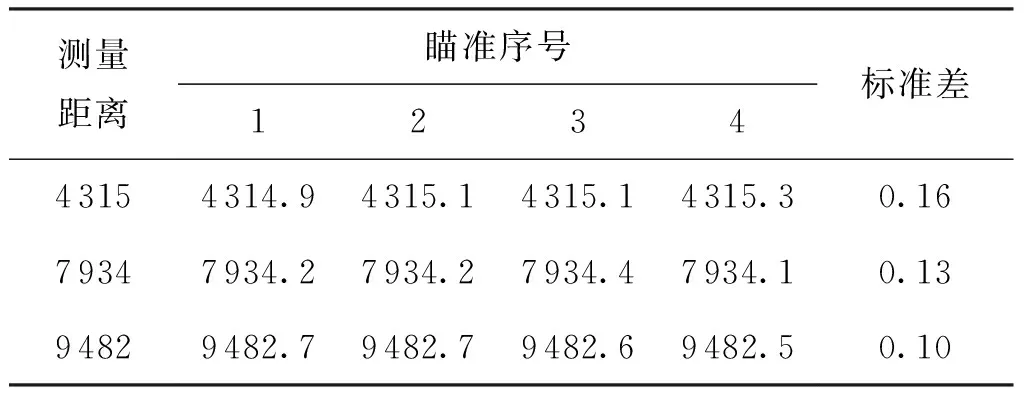
表1 主动扫描瞄准实验结果 mm
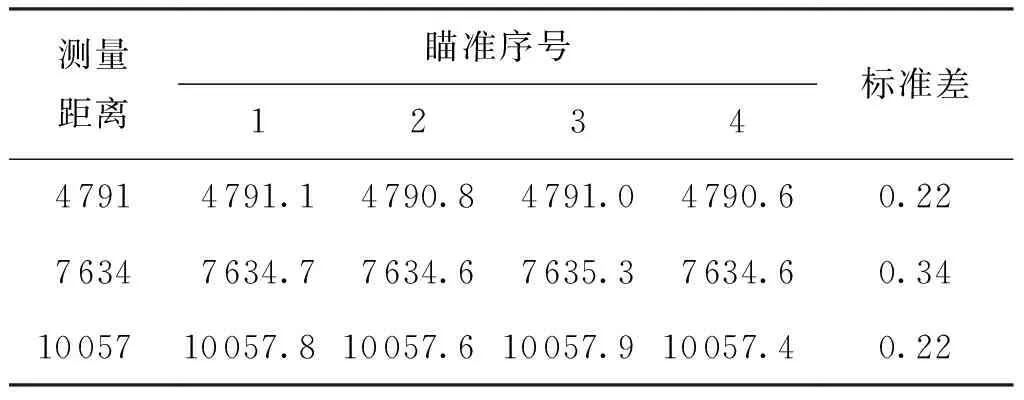
表2 寻心扫描瞄准实验结果 mm
5 结 论
大尺寸测量具有干扰因素多、测量周期长等特点,需要在测量中实时重新标定大空间坐标测量网络的参数,以及时发现并修正测量误差。本文针对大空间坐标测量网络的现场实时标定方法进行了研究,得出以下结论:
(1)提出了模拟基站标定模型,仿真实验表明当测量基站的测距精度为0.5 mm时,测量基站的坐标标定误差均值为2.1 mm。
(2)提出了主动扫描和寻心扫描两种测距瞄准方法,瞄准实验所得测距值标准差分别为0.16 mm和0.34 mm,与测量基站标称的测距标准差相当,表明标定方法是可行的。
[参考文献]
[1] Maisano D A, Jamshidi J, Franceschini F,etal. Indoor GPS: system functionality and initial performance evaluation[J].InternationalJournalofManufacturingResearch, 2008, 3(3): 335-349.
[2] 胡进忠,余晓芬,刘媛媛. 基于激光多边法的坐标测量系统自标定研究[J]. 电子测量与仪器学报, 2014, 28(2): 130-137.
[3] 唐七星,余晓芬,王标. 超大尺寸激光测距大型测控网络研制[J]. 计量学报, 2016, 37(4): 360-365.
[4] 吴斌,丁文,杨峰亭,等. 非正交轴系全站仪坐标测量系统误差分析技术研究[J]. 计量学报, 2017, 38(6): 661-666.
[5] 张红英,余晓芬,王标. 大空间坐标测量网络的精度自适应构建方法[J]. 电子测量与仪器学报, 2016, 30(11): 1664-1670.
[6] 叶声华, 邾继贵, 张滋黎,等. 大空间坐标尺寸测量研究的现状与发展[J]. 计量学报, 2008, 29(z1): 1-6.
[7] Galetto M, Mastrogiacomo L, Pralio B. MScMS-II: an innovative IR-based indoor coordinate measuring system for large-scale metrology applications[J].InternationalJournalofAdvancedManufacturingTechnology, 2011, 152(1-4): 291-302.
[8] 张国雄,林永兵,李杏华,等. 四路激光跟踪干涉三维坐标测量系统[J]. 光学学报,2003, 23(9): 1030-1036.
[9] Camboulives M, Lartigue C, Bourdet P,etal. Calibration of a 3D working space by multilateration[J].PrecisionEngineering, 2016, 44(1): 163-170.
[10] 林永兵,张国雄,李真,等. 四路激光跟踪干涉三维坐标测量系统自标定与仿真[J]. 仪器仪表学报,2003, 24(2): 205-210.
[11] Zhang D F, Rolt S, Maropoulos P G. Modelling and optimization of novel laser multilateration schemes for high-precision applications[J].Meas.Sci.Technol. , 2005, 16 (1): 2541-2547.
[12] Santolaria J, Majarena A C, Samper D,etal. Articulated Arm Coordinate Measuring Machine Calibration by Laser Tracker Multilateration[J].TheScientificWorldJournal, 2014, 2014: 681853-11.
[13] Wendt K, Franke M, Härtig F. Measuring large 3D structures using four portable tracking laser interferometers[J].Measurement, 2012, 45(10): 2339-2345.
[14] Takatsuji T, Koseki Y, Goto M,etal. Restriction on the arrangement of laser trackers in laser trilateration[J].MeasurementSienceandTechnology, 1998, 9(8): 1357-1359.
[15] 胡进忠. 超大尺寸测量网络构建方法研究[D]. 合肥:合肥工业大学,2015.

