数字示波器大触发延迟时间的量子化测量方法

梁志国

(北京长城计量测试技术研究所 计量与校准技术重点实验室， 北京 100095)

1 引 言

人们所处的物质世界是以基本时空来确定与衡量的，三维空间和一维时间所描述的四维世界定义表述了大千世界。因而，时间差的量值至关重要。一些仪器设备，如高度表、雷达、测距机、声纳等，借助于物理原理，利用电磁波、光波、声波等，将空间距离转换成时间差进行测量。更加凸显了时间差精确测量与校准的意义与价值[1～16]。

在时间差测量与校准中，数字示波器的触发延迟具有独一无二的作用。实际上，数字示波器从诞生起就获得广泛应用的原因主要有两点：一是高速宽带的波形测量能力；二是丰富多彩且功能强大的触发功能[10～16]。其主要特征是：(1)具有明确可靠的事件条件捕捉能力；(2)与其它绝大多数仪器设备的触发时开启物理动作不同，数字示波器在开机后实际上一直处于测量并循环记录的工作状态，其触发实际上是结束测量的指令，因而，其触发延迟时间可以是正值(落后于触发条件)，也可以是负值(超前于触发条件)；(3)拥有超长延迟能力，触发延迟时间可以从0 s至几百 s任意可调，具有极高的时间分辨力，可达纳秒量级。

数字示波器触发延迟的计量校准，可使用外接硬件延时器方式进行。其难点主要在于固定延时器有较高准确度，但只能计量校准一些离散点，很难实现宽范围任意时间间隔的计量校准。而间隔可调的延时器，准确度和分辨力较难满足校准要求。

另外一种触发延迟时间的计量校准方法，是使用正弦波条件下的相位差测量方式进行[17～19]，也可获得足够的测量准确度，但其前提条件是延迟时间小于一个正弦波形周期。当其大于所用正弦波形周期时，由于相位差的多值性和周期性，很难直接用来进行触发延迟时间差的精确测量与评价。

本文所指的大触发延迟时间差，即是延迟时间大于激励信号波形周期的条件和情况。由此可见，大触发延迟的精确测量与校准是一个尚待进一步研究解决的问题。

本文后续内容，主要针对数字示波器大触发延迟时间的精确测量与校准问题展开讨论。提出了累积时间法和量子化法两种测量校准方法，其特征是直接使用高精度正弦信号源，用正弦信号的周期作为尺度标准，直接实现大触发延迟时间的精确测量与校准，具有宽广的测量范围和几乎连续的时间分辨力，无需使用外接的延时器，可实现任意触发时间延迟的测量与校准。

2 测量原理

大触发延迟累积法测量的基本思想，是针对大触发延迟时间τ，使用周期为T(频率f=1/T)的正弦波形作为触发激励信号，用正弦激励信号的周期T作为测量触发延迟的尺子。为适应大时间延迟τ的测量，将触发延迟时间分为整数个信号周期部分和小数个信号周期部分的两部分合成。

其中，小数个信号周期部分的延迟使用同频率下相位差测量原理进行测量、拟合、运算处理获得。

关于整数部分的确定，首先，通过将大于激励信号周期T的大触发延迟时间τ分割成多个小于激励信号周期的小触发延迟增量Δτi(Δτi≤T/2)之和，然后，用相位差法分别求得这些小触发延迟增量，最后，通过累加获得大触发延迟的初步测量结果，由此初步测量结果可以获得准确的触发延迟包含的激励信号周期个数m。

将整数部分延迟与小数部分延迟进行叠加合成，获得大触发延迟测量结果。

对于固定的延迟τ时间而言，其所对应的完整信号相位差φ与频率f的关系为：φ=2p f·τ

由于正弦波的周期性，导致相位差的多值性，具有典型的量子化特征，即，人们测量获得的相位差φ，其值域范围为φ∈[0,2p}。φ与φ的关系有：

φ=2p f·τ=φ+2p ·m

(1)

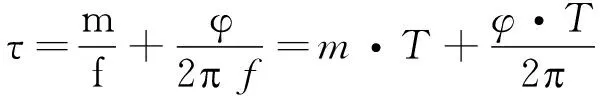
(2)

式中：m为非负整数。

所述整数个信号周期部分整数m的确定，是将待校准延迟时间τ拆分为多个延迟增量Δτi，且使得

Δτi≤T/2

(3)

τ0=0

(4)

τi=τi-1+Δτi, (i=1,2,…,q)

(5)

τ=τq

(6)

(7)

式中：int[*]为取整数运算。

对于被校准的大延迟时间τ，在将其拆分成多个不同的延迟增量Δτi时，Δτi对应的相位差Δτi，其值域范围为Δφi∈[0,p }。为确保整数m的确定不会出现错误。其过程如下：

(1)如图1所示，设定被测量数字示波器的触发条件，根据被测量数字示波器触发信号的幅度范围和触发信号频率范围，选取正弦信号源的信号幅度，信号频率为f，通过三通将正弦波信号同时加载到数字示波器的测量通道和触发输入端。

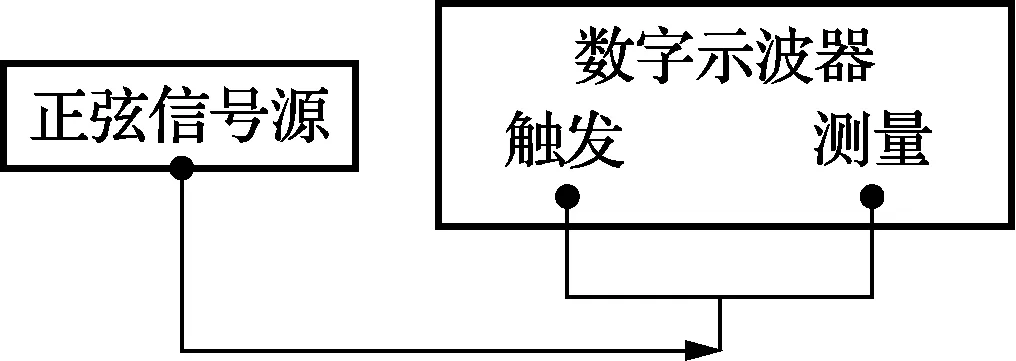
图1 触发延迟测量原理框图

设定触发延迟为τ0=0，触发测量并记录采样波形序列，获得采样时间点t0,1,t0,2,…,t0,n上的等间隔采样序列为x0,1,x0,2,…,x0,n。用四参数正弦波拟合方法进行最小二乘波形拟合[20, 21]，其函数表达式为：

(8)

拟合残差均方根值为：

(9)

(2)其它条件不变，设定触发延迟为τ1=τ0+Δτ1，Δτ1≤T/2，触发测量并记录采样波形序列，获得采样时间点t1,1,t1,2,…,t1,n上的等间隔采样序列为x1,1,x1,2,…,x1,n。用四参数正弦波拟合方法进行最小二乘拟合，其拟合曲线的函数表达式为：

(10)

拟合残差均方根值为：

(11)

则，待测触发延迟Δτ1对应的相位差Δφ1为：

Δφ1=2p ·f·Δτ1=φ1-φ0

(12)

(13)

(3)其它条件不变，设定触发延迟为τ2=τ1+Δτ2，Δτ2≤T/2，触发测量并记录采样波形序列，获得采样时间点t2,1,t2,2,…,t2,n上的等间隔采样序列为x2,1,x2,2,…,x2,n。用四参数正弦波拟合方法进行最小二乘拟合，其拟合曲线的函数表达式为：

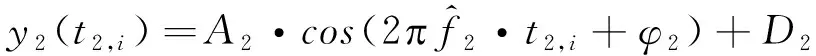
(14)

拟合残差均方根值为：

(15)

则，待测触发延迟Δτ2对应的相位差Δφ2为：

Δφ2=2p ·f·Δτ2=φ2-φ1

(17)

(4)在新的延迟增量上重复上述(3)的过程，依次获得Δτ3,Δτ4, …,Δτq，τ=τq。

即，其它条件不变，设定触发延迟为τk=τk-1+Δτk，Δτk≤T/2，触发测量并记录采样波形序列，获得采样时间点tk,1,tk,2,…,tk,n上的等间隔采样序列为xk,1,xk,2,…,xk,n。用四参数正弦波拟合方法进行最小二乘拟合，其拟合曲线的函数表达式为：

(18)

拟合残差均方根值为：

(19)

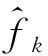
则，待测触发延迟Δτk对应的相位差Δφk为：

Δφk=2p ·f·Δτk=φk-φk-1

(20)

(21)

(23)

3 实验验证

接线如图1所示。使用DSO8104型数字示波器作为被测对象，其A/D位数8 Bit，频带宽度1 GHz，存储深度16 M，共4个测量通道。用通道 3作为测量通道。

设置其幅度量程为±1.2 V(300 mV/div)，直流偏置offset=-2 mV，采集速率v=10 kSa/s(100 ms/div)，通道采集数据个数n=20 022，触发电平202 mV, 上升沿触发，待测的触发延迟τ=1.1 s。

用HP3325B合成信号源产生的正弦信号波形作为标准激励[22]，根据待测触发延迟，选取等间隔延迟增量Δτi=0.05 s，激励正弦波形周期T>Δτi，频率为9 Hz，峰值幅度0.5 V。

执行上述步骤(1)～(5)，获得Δτi实测值为： 0.049 9, 0.050 1, 0.050 1, 0.049 9, 0.050 1, 0.050 0, 0.050 0, 0.049 6, 0.050 4, 0.050 1, 0.049 9, 0.050 0, 0.050 2, 0.050 0, 0.049 9, 0.050 0, 0.050 1, 0.049 7, 0.049 8, 0.050 7, 0.049 8, 0.050 0 s。

其中，取τ0、τ1、τ2、τ3等4条曲线的局部显示如图2，可见，相邻曲线之间的相位延迟略小于180°。

图2 4条不同触发延迟曲线时序关系

T=1/9，按式(7)计算得：m=9。

由直接相位差法计算得小数部分延迟：

则，由式(23)可得大触发延迟测量结果为：

4 不确定度分析

直接使用相位差法进行触发延迟时间差的测量时，其不确定度评定可以参照文献[18]执行，本文不再赘述。获得的参考结论是，其通常仅有2～3位有效数字。

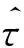
5 讨 论

本文所述方法，可以实现数字示波器的大触发延迟的测量，其溯源渠道为正弦信号频率，优点是可以实现未知任意量值的触发延迟时间差的精确测量。其不足之处主要体现在为了应对大延迟时间差问题，需要将大延迟时间分割成众多小延迟增量之和，因而造成测量工作量巨大。当触发延迟时间非常大时，尤其如此。例如延迟时间为上百秒时，需要数百次触发测量才能实现最终结果。其中最主要的目的仅仅是准确判定整数个激励波形周期m而已。解决之道是选取尽量低的激励信号频率和尽量大的触发延迟增量，从而降低工作量。

在计量校准工作中，通常的大延迟时间差是拥有足够准确度的已知量值，人们仅仅是需要通过计量校准工作确定其实际值与标称值之间的差异而已。此时，通常人们可以不必将其分割成众多微小延迟的累积，而是在承认其拥有足够准确度的基础上对其进行计量溯源，此时，可以使用其给定的标称值τq直接使用式(7)计算获得m值，然后，直接使用0延迟时间的采样序列和τq延迟时间的采样序列之间的相位差获得延迟时间差的小数部分，用式(23)计算合成被测量的大触发延迟即可。由此可望极大降低计量校准的工作量。

另外需要注意的一点是，本文所述的大触发延迟，是与0触发延迟相比较而产生的增量延迟，并非是与定义触发点相比的绝对延迟，有关绝对延迟的测量实际上是要参照本文方法获得的延迟，结合0延迟时其实际相对于定义触发点的绝对延迟合成而得，相关文献给出了0延迟时其相对于定义触发点的绝对延迟的测量方法，本文不再赘述。

6 结 论

综上所述，本文所述方法主要是针对大触发延迟时间测量中，该被测量的大延迟时间在与使用直接相位差测量法获得的时间差相比，一定相差整数个激励波形周期这一量子化特征，尝试以累积方法判定该整数值，然后与用直接相位测量法获得的时间差相合成，最终获得数字示波器大触发延迟的测量结果。该方法可将触发延迟时间差溯源到激励正弦信号的频率量值上，无须使用外接硬件延时器，尤其适合于计量部门和用户对数字示波器大触发延迟量值实现精确测量与校准。

[参考文献]

[1] Gao Y K, Zhang T T, Pokharel P,etal. Pseudo Functional Path Delay Test through Embedded Memories[J].JournalofElectronicTesting, 2015, 31(1): 35-42.

[2] Liu T Q, Zhou Y B, Liu Y,etal. Harzard-Based ATPG for Improving Delay Test Quality[J].JournalofElectronicTesting, 2015, 31(1): 27-34.

[3] Long X, Arends J B, Aarts R M,etal. Time delay between cardiac and brain activity during sleep transitions[J].AppliedPhysicsLetters, 2015, 106(14): 143702-1-4.

[4] Li H M, Liu S B, Liu S Y,etal. Electromagnetically induced transparency with large delay-bandwidth product induced by magnetic resonance near field coupling to electric resonance[J].AppliedPhysicsLetters, 2015, 106(11): 114101-1-4.

[5] Ban Y, Wang L J, Chen X. Tunable delay time and Hartman effect in graphene magnetic barriers[J].JournalofAppliedPhysics, 2015, 117(16): 164307-1-6.

[6] Jing Q, Zhang X, Wei W,etal. Power dependent pulse delay with asymmetric dual-core hybrid photonic crystal fiber coupler[J].OpticsandLaserTechnology, 2014, 55(2): 26-36.

[7] Xiang S Y, Pan W, Zhang L Y,etal. Phase-modulated dual-path feedback for time delay signature suppression from intensity and phase chaos in semiconductor laser[J].OpticsCommunications, 2014, 324(324): 38-46.

[8] Xu Y H, Xie C R, Tong D B. Adaptive synchronization for dynamical networks of neutral type with time-delay[J].Optik-InternationalJournalforLightandElectronOptics, 2014,125(1): 380-385.

[9] Singh H,Sheetal A, Kumar A.Impact of interferometer delay time on the performance of ODSB-SC RoF system with wavelength interleaving[J].Optik-InternationalJournalforLightandElectronOptics, 2014, 125(9): 2057-2061.

[10] 冯为蕾，王福娟，曾万祺，等.应用于LIBS的CCD光谱测量系统[J].激光与光电子学进展，2013，50(1)：196-202.

[11] 梁境锋，李光灿，杜勇，等.TSA线性阵列的脉冲辐射特性分析[J].电子测量技术，2012，35(8)：38-41.

[12] 顾军.频率捷变信号源的捷变合成研究及实现 [J].电子测量技术，2010，33(6)：17-19.

[13] 卫兵，卿燕玲，李洪涛,等.开关触发延迟时间和抖动测量的不确定度分析[J].强激光与粒子束，2010，22(7)：1649-1652.

[14] 赵娟，曹科峰，曹宁翔,等.脉冲氙灯放电闪光仪 [J].国外电子测量技术，2009，28(6)：52-54.

[15] 程度，耿春萍，张治.逻辑分析仪在数字电路测试中的触发选择[J].现代电子技术，2007，30(13)：160-162.

[16] 武锦辉，李仰军，赵冬娥.激光测速靶连发弹丸速度测试系统[J].兵工自动化，2005，24(4)：16-17.

[17] 梁志国.数字存储示波器触发点电平和延迟的精确校准[J].仪器仪表学报，2011，32(6): 1403-1409.

[18] 梁志国，孟晓风.波形记录仪触发延迟的测量不确定度评定[J].计量学报，2011，32(4)：361-367.

[19] 梁志国，孟晓风.波形记录仪触发延迟线性的实验研究[J].计测技术，2009，29(5)：4-7.

[20] 梁志国.数据采集系统校准中的若干问题研究[D].北京：北京航空航天大学，2009.

[21] 国家质量技术监督局.JJF 1057—1998 数字存储示波器[S]. 1999.

[22] Hewlett Packard Company. HP 3325B Synthesizer/Function Generator Operating Manual [Z].1990.