马尔科夫跳变系统的不定平均场随机线性二次最优控制问题

,,(山东科技大学 数学与系统科学学院，山东 青岛 266590)

近几十年来，马尔科夫跳变系统获得极大关注，并被应用于各个领域，例如航天器设计、太阳能站、卫星动态系统、证券投资组合最优化以及通讯网络等。文献[1]中有很多关于离散时间马尔科夫跳变系统的基础知识，文献[2]则讲解关于最优控制的基本问题和应用。文献[3]是随机奇异系统的线性二次帕累托最优控制问题，文献[4]研究随机的离散时间线性二次最优控制问题，文献[5]和[6]分别研究离散时间平均场线性二次最优控制问题对于有限和无限时间的情况。

最优控制理论由经典变分学发展起来，其历史可追溯到360年前。但是直到上世纪60年代，人们才真正对其产生兴趣[7]。文献[8]利用一种非协调有限元局部稳定化方法解决Navier-Stokes方程的最优化问题。动力学系统的数学模型为线性方程,所取的性能指标为状态变量与控制变量的二次型函数,这种动态系统的最优化问题称为线性二次型(linear quadratic, LQ)问题。由于LQ问题的最优解具有统一的解析表达式,且可得到一个线性的状态反馈控制律,便于计算和实现闭环反馈控制,从而成为最优控制理论及应用中最成熟的部分[9]。文献[10]研究一类含消费、寿险和投资的随机最优控制问题。

马尔科夫跳系统作为一类典型的混杂动态系统，由于其强大的建模能力在各个领域已经得到广泛的应用[11]。文献[12]研究带有马尔科夫跳变参数的连续时间线性二次问题。文献[13]讨论连续时间马尔科夫跳变系统的时变问题，通过一个带有马尔科夫跳变的性能指标来解决不定线性二次最优控制问题，并研究了代替平均差的标准。

本文研究一类离散时间平均场随机线性二次最优控制问题。平均场能够简化对复杂问题的研究，把一个高次、多维的难以求解的问题转化为一个低维问题。近来，平均场类型的随机最大值原理获得广泛关注，文献[14]研究局部信息下平均场类型最优控制问题的随机最大值原理。文献[15]在传统传染病SIR模型的基础上，利用平均场改进为一个基于用户影响力的信息传播模型。文献[16]通过变分法，推导出平均场类型的随机最大值原理的最优化系统是一个线性平均场前后随机差分方程。

文献[17]针对跳变系统参数矩阵不确定的情况，引进一种新的分解技术，将不同时刻下的系统综合考虑，以矩阵块的方式给出最优控制的表达式。与文献[17]相比较，本研究将系统和性能指标的加权矩阵推广到不定的情况，首先定义一个差分黎卡提方程，并得到最优控制存在的充分条件是黎卡提方程可解，给出最优控制的一般表达式以及不考虑平均场时的特殊形式，可视为对文献[17]结果的一个推广。

1 问题阐述与定义准备

研究如下带有乘性噪音的系统：

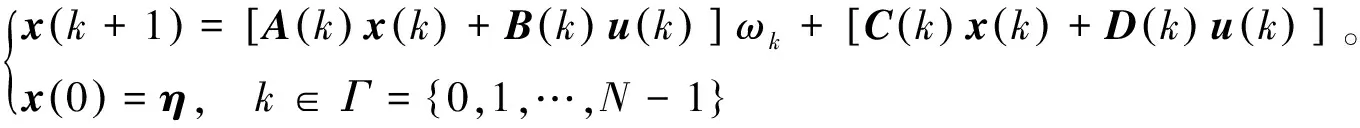
(1)

其中：A，C∈Rn×n和B，D∈Rn×m都是对称矩阵，x(k)和u(k)分别是状态变量和控制变量。噪声扰动参数ω≡{ωk}以及状态初始值η均定义在完备概率空间(Ω,F,P)上。状态初始值η是0时刻的状态值，即η=x(0)。噪声扰动参数ω是一个有限二阶矩的鞅差分序列，并且E[ωk+1|Fk]=0，其中Fk是由集合{x(0),ωl,θl,l=0,1,…,k}所产生的σ-代数，并且满足:

(2)

考虑下面的性能标准:

J(x(0),u(k),θ0)

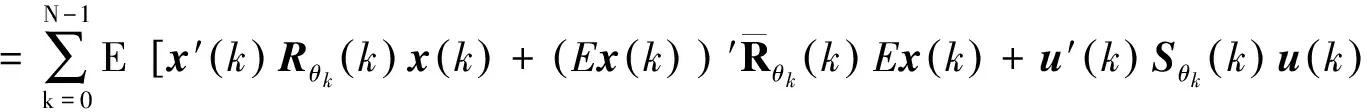
(3)

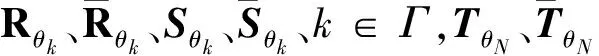
pij=P(θk+1=j|θk=i),i,j∈M,k∈Γ。

(4)

E是期望算子，对于k=0,1,…,N，记：

定义1.1(MF-LQ) 对于任意的初始值η，如果存在u0(k)∈U使得:

(5)

其中，U是可容许控制集，则称u0(k)是MF-LQ问题的最优控制。

本研究系统和性能指标的加权矩阵可以是不定的，为方便后续使用，引入广义逆矩阵的定义。

定义1.2[18]给定矩阵Q∈Rm×n，则存在一个唯一的矩阵Q+∈Rn×m，称为Q的广义逆矩阵，使得:

(6)

引理1.3[18]给定对称矩阵L，M，N，则矩阵方程LXM=N有解X的充要条件是:

LL+NMM+=N，

并且解的一般表达式为X=L+NM++Y-L+LYMM+，其中Y是合适维数的任意矩阵。

2 主要结果

为定义系统(1)的广义黎卡提差分方程，先引入两个等式

E[x′(N)PθN(N)x(N)]-E[x′(0)Pθ0(0)x(0)]

(7)

以及

(8)

通过噪声扰动参数的性质以及简单的计算有：

E[x′(k+1)Pθk(k+1)x(k+1)|Fk]

=x′(k)[A′(k)E(Pθk(k+1))A(k)+C′(k)E(Pθk(k+1))C(k)]x(k)

+2x′(k) [A′(k)E(Pθk(k+1))B′(k) +C′(k)E(Pθk(k+1))C′(k)]u(k)

+u′(k)[B′(k)E(Pθk(k+1))B′(k)+D′(k)E(Pθk(k+1))D′(k)]x(k),

(9)

故有:

E[x′(N)PθN(N)x(N)]-E[x′(0)Pθ0(0)x(0)]

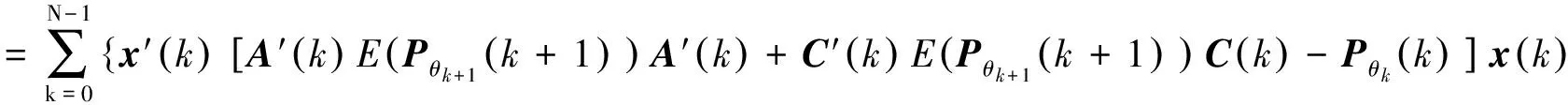
+2x′(k)[A′(k)E(Pθk+1(k+1))B(k)+C′(k)E(Pθk+1(k+1))D(k)]u(k)

+u′(k)[B′(k)E(Pθk+1(k+1))B(k)+D′(k)E(Pθk+1(k+1))D(k)]u(k)},

(10)

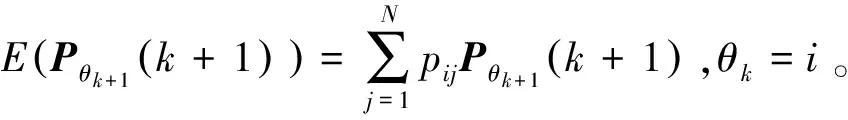
(11)

通过式(3)以及式(7)、(8)、(10)、(11)，有：

J(x(0),u(k),θ0)

-Pθk(k)]x(k)+2x′(k) [A′(k)E(Pθk+1(k+1))B(k)+C′(k)E(Pθk+1(k+1))D(k)]u(k)

+u′(k) [Sθk(k)+B′(k)E(Pθk+1(k+1))B(k) +D′(k)E(Pθk+1(k+1))D(k)]u(k)

(12)

定义2.1给出下面的约束差分方程：

(13)

其中

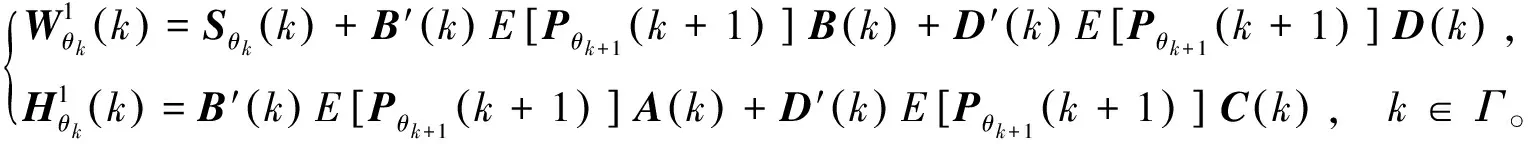
(14)

和

(15)

其中

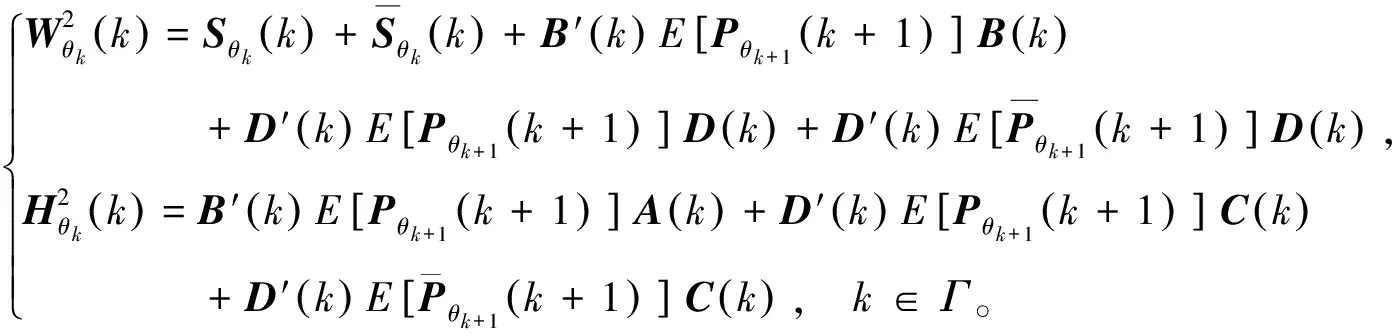
(16)

称为乘性噪声系统的广义差分黎卡提方程。

定理2.2对于线性二次最优化问题(1)、(3)、(5)，最优控制:

(17)

(18)

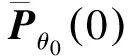
证明：通过简单的完全平方计算以及定义2.1，(12)式可以转化为:

J(x(0),u(k),θ0)

×E(Pθk + 1(k+ 1))C(k)](x(k)-Ex(k))+ 2(x(k)-Ex(k))[A′(k)

×E(Pθk + 1(k+ 1))B(k) +C′(k)E(Pθk + 1(k+ 1))D(k)](u(k)-Eu(k))

+ (u(k)-Eu(k))[Sθk(k) +B′(k)E(Pθk + 1(k+ 1))B(k) +D′(k)

+A′(k)E(Pθk + 1(k+ 1))A(k)]Ex(k) + (Ex(k))[C′(k)(E(Pθk + 1(k+ 1))

+E(x′(0)Pθ0(0)x(0))

(19)

令

(20)

求解方程组(20)，得最优控制的表达式为:

(21)

相应的性能指标的最小值：

(22)

证明结束。

注释2.3特别地，当系统(1)、(4)、(5)中加权矩阵正定时，并且系统中不再考虑跳变参数时，定理2.2变为文献[23]定理3.1。

推论2.4当性能指标中不考虑平均场，对应的最优控制为:

(23)

相应性能指标最小值:

(24)

证明：通过定义2.1 和简单的完全平方计算，(12)式可以转换为:

J(x(0),u(k),θ0)

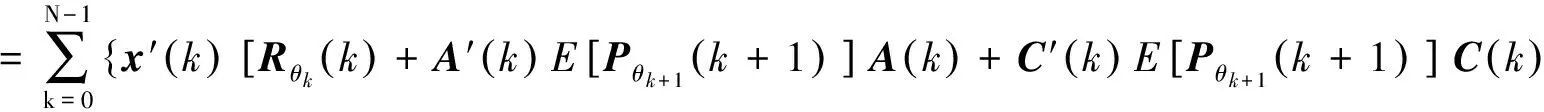
-Pθk(k)]x(k)+2x′(k) [A′(k)E[Pθk+1(k+1)]B(k)+C′(k)E[Pθk+1(k+1)]D(k)]u(k)

+u′(k) [Sθk(k)+B′(k)E[Pθk+1(k+1)]B(k)+D′(k)E[Pθk+1(k+1)]D(k)]u(k)}

+E[x′(0)Pθ0(0)x(0)]

+E[x′(0)Pθ0(0)x(0)],

(25)

则最优控制为:

(26)

相应性能指标最小值:

(27)

证明结束。

3 数值例子

这一部分研究一个数值例子。对于给定的系统:

考虑下面的性能指标:

其中，马尔科夫链θ的取值为1，2，转移概率矩阵为:

其中

pij=p(θk+1=j|θk=i),i,j=1,2,k=0,1,2。

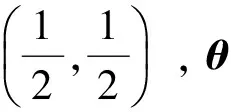
对于任意的k=0,1，2，当θk=1时，

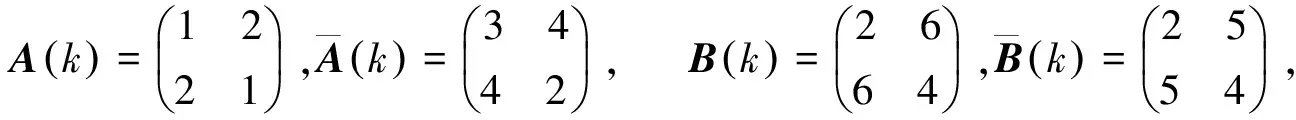
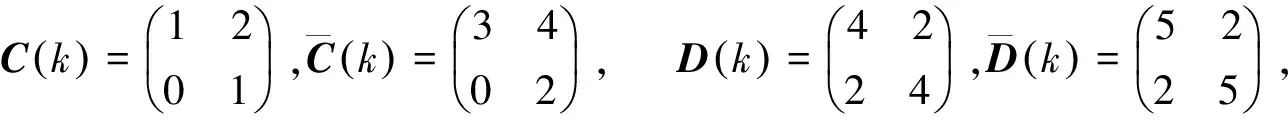
对于任意的k=0,1,2，当θk=2时，

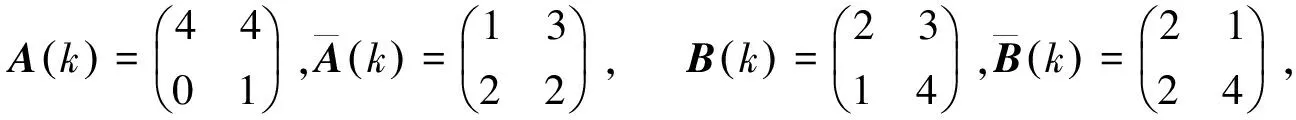
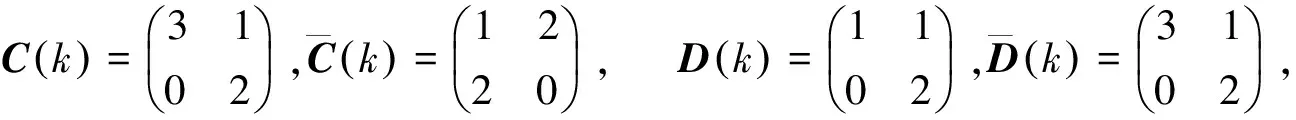
通过式(13)～(16)，对于任意的k=0,1,2，当θk=1时，有:

最优控制(17)式中的对应系数如下:

当对于任意的k=0,1,2，当θk=2时，有:

最优控制(17)式中的对应系数如下:

则最优控制和性能指标的表达式如下:

以及

和

令x(0)=(0,1)′，则

4 总结

研究了乘性噪声系统的不定平均场随机线性二次最优控制问题，系统和性能指标中的参数矩阵允许是不定的，首先定义一种广义差分黎卡提差分方程，证明其可解性是最优控制存在的充分条件。其次，推导出最优控制的一般表达式。最后，给出没有平均场时最优控制的特殊形式。

参考文献：

[1]COSTA O L V,FRAGOSO M D,MARQUES R P.Discrete-time Markov jump linear systems[M].London：Springer-Verlar,2005:916-917.

[2]解学书.最优控制理论与应用[M].北京:清华大学出版社,1986.

[3]ZHANG W H,LIN Y N,XUE L G.Linear quadratic Pareto optimal control problem of stochastic singular systems[J].Journal of the Franklin Institute,2017,354(2):1220-1238.

[4]LIU X K,LI Y,ZHANG W H.Stochastic linear quadratic optimal control with constraint for discrete-time systems[J].Applied Mathematics and Computation,2014,228:264-270.

[5]ELLIOTT R,LI X,NI Y H.Discrete time mean-field stochastic linear-quadratic optimal control problem[J].Automatica,2013,49:3222-3233.

[6]NI Y H,ELLIOTT R,LI X.Discrete time mean-field stochastic linear-quadratic optimal control problem,II:Infinite horizon case[J].Automatica,2015,57:65-77.

[7]韦兰用.最优控制问题研究综述[D].长春:吉林大学,2006.

[8]覃艳梅,李辉,冯民富.Navier-Stokes方程最优控制问题的一种非协调有限元局部稳定化方法[J].应用数学和力学,2016,37(8):842-855.

QIN Yanmei,LI Hui,FENG Mingfu.A local stabilization nonconforming finite element method for the optimal control of Navier-Stokes equations[J].Applied Mathematics and Mechanics,2016,37(8):842-855.

[9]马宏基.不定随机线性二次最优控制若干问题的研究[D].青岛:山东科技大学,2007.

[10]梁宗霞,赵笑阳.一类含消费、寿险和投资的随机最优控制问题[J].中国科学,2016,46(12)：1863-1882.

LIANG Zongxia,ZHAO Xiaoyang.Optimal investment,consumption and life insurance under stochastic framework[J].Science China,2016,46(12):1863-1882.

[11]李繁飙.半马尔科夫跳变系统的分析和综合[D].哈尔滨:哈尔滨工业大学,2015.

[12]ZHOU J.On stochastic Riccati equations for the stochastic LQR problem[J].Systems & Control Letters,2005,54(2):119-124.

[13]DRAGAN V,MOROZAN T.The linear quadratic optimization problems for a class of linear stochastic systems with multiplicative white noise and Markovian jumping[J].IEEE Transactions on Automatic Control,2004,49(5):665-675.

[14]WANG G C,ZHANG C H,ZHANG W H.Stochastic maximum principle for mean-field type optimal control under partial information[J].IEEE Transactions on Automatic Control,2014,59(2):522-528.

[15]肖云鹏,李松阳,刘宴兵.一种基于社交影响力和平均场理论的信息传播动力学模型[J].物理学报,2017,66(3):1-13.

XIAO Yunpeng,LI Songyang,LIU Yanbing.An information diffusion dynamic model based on social influence and mean-filed theory[J].Acta Physica Sinica,2017,66(3):1-13.

[16]YONG J M.A linear quadratic optimal control problem for mean-field stochastic differential equations[J].SIAM Journal on Control Optimization,2013,51(4):2809-2838.

[17]NI Y H,LI X,ZHANG J F.Mean-field stochastic linear-quadratic optimal control with Markov jump parameters[J].Systems & Control Letters,2016,93:69-76.

[18]RAMI M A,CHEN X,ZHOU X Y.Discrete-time indefinite LQ control with state and control dependent noises[J].Journal of Global Optimization,2002,23:245-265.