时标上障碍带条件下p-Laplacian方程两点边值问题解的存在性
,(山东科技大学 数学与系统科学学院,山东 青岛 266590)
常微分方程是伴随着微积分的产生和发展而逐渐成长起来的一门历史悠久的学科。在数学学科内部的许多分支中,常微分方程是常用的重要工具之一。由于应用领域的不断扩大和新理论生长点的不断涌现,这一古老学科的发展至今仍充满着生机与活力。微分方程边值问题是一个微分方程和一组边界条件形成的方程组,边值问题的解通常是符合约束条件的微分方程的解。在物理学、生物学等中都经常遇到边值问题,例如波动方程等。
常微分方程边值问题是微分方程研究领域中一个十分重要而热门的话题。早在1994年,Kelevedjiev[1]运用Leary-Schauder原理讨论了障碍带条件下非线性二阶两点边值问题x′′(t)=f(t,x(t),x′(t)),t∈(0,1)分别在Dirichlet边界条件x(0)=A,x(1)=B、Neumann边界条件x(0)=A,x(1)=B以及混合边界条件x(0)=A,x′(1)=B、x′(0)=A,x(1)=B下解的存在性问题,得出了函数f在满足一类符号条件下解的存在性定理。
在时标理论未出现前,一些连续变化的现象或过程可以用微分方程去刻画;对于某些离散的现象或变化过程,则用差分方程去描述,但对于一些既包括连续又包括离散状态的数学模型却无从下手。时标理论提供了一种研究实际生活中许多没有规律现象的新方法,时标理论的出现,引起众多学者的关注和研究。结合时标理论,Ma和Luo[3]运用Leary-Schauder原理及时标上函数的相关性质,并运用截断函数的技巧,结合文献[1]中所用方法研究了时标上边值问题
xΔΔ(t)=f(t,x(t),xΔ(t)),t∈[0,1]T,x(0)=0,xΔ(σ(1))=0
解的存在性。若将时标T取为实数集R,即为文献[1]中所研究的Dirichlet问题。
2014年,Ma等[4]运用拓扑横截定理研究了障碍带条件下φ-Laplace方程两点边值问题
(φ(u′))′=f(t,u,u′),t∈(0,1),u(0)=A,u′(1)=B
解的存在性,该文用更一般的增算子代替了p-Laplace算子,若是用p-Laplace算子作用,便是本文将时标T推广到实数集R的特殊情况。另外,对于不同边值条件下解的存在性,还可以运用不动点定理、拓扑度方法、上下解方法和非线性泛函分析等方法来研究,具体可以参考文献[5-8,11-20]。
受以上文章的启发,本文研究时标上障碍带条件下一类p-Laplace方程两点边值问题
(φp(xΔ(t)))Δ=f(t,x(t),xΔ(t)),t∈(0,1),
(1)
x(0)=xΔ(σ(1))=0,
(2)
或者
xΔ(σ(0))=x(1)=0,
(3)

1 预备知识
时标T是指实直线R上的一个非空子集,当T取R时,时标T上的微分方程边值问题即是常微分方程边值问题。
定义1对t∈T,规定infφ=maxT。定义前跳跃算子σ:T→T为
σ(t)=inf{τ>t|τ∈T}。
对t∈T,设supφ=minT,定义后跳跃算子ρ:T→T为
ρ(t)=sup{τ 当σ(t)>t时,称t是右离散的:当σ(t)=t时,称t是右稠密的。同样,当ρ(t) T上的子集TK,TK分别定义为:如果T有左离散的最大值t1,则TK=T-{t1},否则TK=T;如果T有右离散的最小值t2,则TK=T-{t2},否则TK=T。 T上的开区间(a,b)定义为(a,b)={t∈T|a 定义1.2设f:T→R,t∈TK。如果有R中的数fΔ(t),使得对∀ε>0,存在t的一个邻域U,使得对所有的s∈U,都有 |f(σ(t))-f(s)-fΔ(t)(σ(t)-s)|≤ε|σ(t)-s|, 则称fΔ(t)为f在t点的Δ-导数。若对所有的t∈TK,fΔ(t)都存在,称f在TK上是Δ-可导的。 定义1.3若恒有FΔ(t)=f(t),t∈TK,则Δ-积分定义为 引理1.1[9]设f:T→R,t∈TK,则以下各条成立: 1)如果fΔ(t)存在,则f在t点处连续; 4)如果fΔ(t)存在,则 f(σ(t))=f(t)+(σ(t)-t)fΔ(t)。 引理1.2[10]设X,Z为实向量赋范线性空间,L:domL⊂X→Z是一个指标为0的Fredhoml算子。假定Ω⊂X是有界开子集,N:Ω→Z是一个L-紧算子。如果kerL={0},0∈Ω且对所有的(u,λ)∈(domL∩∂Ω)×(0,1), Lu-λNu≠0, 定理2.1设f:[0,σ(1)]×R→R连续,L:D→C[0,1],Lx=(φp(xΔ(t)))Δ,若存在常数C使得对边值问题 Lx(t)=λf(t,x(t,),xΔ(t)),t∈(0,1),x∈D,λ∈(0,1) (2.1) 证明:首先,证明L是一一映射。在边值条件(1.2)下,由Lx=0可得到x(t)≡0,即kerL={0}。因此L是一一映射。令N:C2[0,σ2(1)]→C[0,1],G:C[0,1]→C2[0,σ2(1)],且 (Nx)(t)=f(t,x(t),xΔ(t)),t∈[0,σ(1)], , 则LGy=y,y∈C[0,1],GLx=x,x∈D,于是GL是零指标的Fredholm映射。从而得出GN:C2[0,σ2(1)]→C2[0,σ2(1)]是GL紧映射。 定理2.2设f:[0,σ(1)]×R2→R连续,假设存在Li,i=1,2,3,4,满足L2>L1≥0,L3 f(t,u,p)≥0, (t,u,p)∈[0,1]×R×[L1,L2], (2.2) f(t,u,p)≤0, (t,u,p)∈[0,1]×R×[L3,L4], (2.3) 则问题(1.1),(1.2)在C2[0,σ2(1)]中至少有一个解。 证明:考虑同伦族问题 (φp(xΔ(t)))Δ=λf(t,x(t),xΔ(t)),t∈[0,1], (2.4) x(0)=xΔ(σ(1))=0。 (2.5) 由定理2.1知,若(2.4),(2.5)的所有可能解x在C2[0,σ2(1)]中有一个不依赖于λ∈(0,1)的先验界,则问题(1),(2)在C2[0,σ2(1)]中有解。 首先估计xΔ(t)的范数。假设集合 S0={t∈[0,σ(1)]|L1 S1={t∈[0,σ(1)]|L3≤xΔ(t) (2.6) 则由xΔ(t)的连续性可知,可取t0∈(t0,1]∩S0,但对t∈S0,有 (φp(xΔ(t)))=λf(t,x(t),xΔ(t))≥0, 所以有 即 xΔ(t)≥xΔ(t0),t∈(t0,1]。 特别地,xΔ(σ(1))≥xΔ(t0)>L1≥0,这与边值条件xΔ(σ(1))=0矛盾。所以S0=Ø。同理可证S1=Ø。 结合xΔ(σ(1))=0以及xΔ(t)的连续性可知 |xΔ(t)|0≤C,t∈[0,σ(1)], (2.7) 其中C=max{|L1|,|L4|}。 另一方面,由式(2.7)知 对t=σ2(1), x(σ2(1)) =x(σ(1))+xΔ(σ(1))(σ2(1)-σ(1)) ≤L1σ(1)+L1(σ2(1)-σ(1)) =L1(σ2(1)), x(σ2(1)) =x(σ(1))+xΔ(σ(1))(σ2(1)-σ(1)) ≥L4σ(1)+L4(σ2(1)-σ(1)) =L4(σ2(1)), 从而有 L4(σ2(1))≤x(t)≤L1(σ2(1)),t∈[0,σ2(1)]。 综上可得 |x|0≤Cσ2(1),t∈[0,σ2(1)]。 类似的,可得如下定理: 定理2.3设f:[0,σ(1)]×R2→R连续,假设存在Li,i=1,2,3,4,满足L2>L1≥0,L3 f(t,u,p)≤0, (t,u,p)∈[0,1]×R×[L1,L2], f(t,u,p)≥0, (t,u,p)∈[0,1]×R×[L3,L4], 则问题(1),(3)在C2[0,σ2(1)]中至少有一个解。 考虑如下边值问题 (φp(xΔ(t)))=(xΔ(t))2-5xΔ(t)+4,t∈[0,1], x(0)=xΔ(σ(1))=0, 参考文献: [1]KELEVEDJIEV P.Existence of solutions for two-point boundary value problems[J].Nonlinear Analysis,1994,22(2):217-224. [2]KELEVESJIEV P,BOJERIKOV S.On the solvability of a boundary value problem forp-Laplacian differential equations[J].Electronic Journal of Qualitative Theory of Differential Equations,2017(8):1-9. [3]MA R,LUO H.Existence of solutions for a two-point boundary value problem on time scales[J].Applied Mathematics and Computation,2004,150(1):139-147. [4]MA R,ZHANG L,LIU R.Existence results for nonlinear problems withφ-Laplacian[J].Electronic Journal of Qualitative Theory of Differential Equations,2015(22):1-7. [5]KELEVEDJIEV P S,TERSIAN S A.The barrier strip technique for a boundary value problem withp-laplacian[J].Electronic Journal of Differential Equations,2013(28):1-8. [6]GOODRICH C S.The existence of a positive solution to a second-order delta-nablap-Laplacian BVP on a time scale[J].Applied Mathematics Letters,2012,25(2):157-162. [7]BAI Z,SUN W,ZHANG W.Positive solutions for boundary value problems of singular fractional differential equations[J].Abstract and Applied Analysis,2013(11):5545-5550. [8]WANG D,GUAN W.Multiple positive solutions for third-orderp-Laplacian functional dynamic equations on time scales[J].Advances in Difference Equations,2014(1):242. [9]GARWAL R P,BOHNER M.Basic calculus on time scales and some of its applications[J].Results in Mathematics,1999,35(1/2):3-22. [10]BAI Z,LIANG X,DU Z.Triple positive solutions for some second-order boundary value problem on a measure chain[J].Computers & Mathematics with Applications,2007,53(12):1832-1839. [11]武华华,孙苏菁.基于变分方法的四阶边值问题的多重正解[J].山东科技大学学报(自然科学版),2014,33(2):96-99. WU Huahua,SUN Sujing.Based on the variational method of the Mmultiple positive solutions for a fourth-order boundary value via variation method[J].Journal of Shandong University of Science and Technology (Natural Science),2014,33(2):96-99. [12]董晓玉,白占兵,张伟.具有适型分数阶导数的非线性特征值问题的正解[J].山东科技大学学报(自然科学版),2016,35(3):85-91. DONG Xiaoyu,BAI Zhanbing,ZHANG Wei.Positive solutions for nonlinear eigenvalue problems with conformable fractional differential derivatives[J].Journal of Shandong University of Science and Technology (Natural Science),2016,35(3):85-91. [13]赵聪,崔玉军.非线性四阶两点边值问题的单调迭代[J].山东科技大学学报(自然科学版),2016,35(6):108-113. ZHAO Cong,CUI Yujun.Monotone iterative technique for nonlinear four-order two point boundary value problem[J].Journal of Shandong University of Science and Technology (Natural Science),2016,35(6):108-113. [14]秦伟.障碍带条件下四阶三点边值问题解的存在性[J].山东科技大学学报(自然科学版),2008,27(3):96-101. QIN Wei.The existence of solutions for fourth-order three-point BVPs under the barrier strips conditions[J].Journal of Shandong University of Science and Technology (Natural Science),2008,27(3):96-101. [15]ATICI F M,GUSEINOV G S.On Greens functions and positive solutions for boundary value problems on time scales[J].Journal of Computatioal and Applied Mathematics,2002,141(1):75-99. [16]LIU Y J.Non-homogeneous boundary-value problems of higher order differential equations withp-Laplacian[J].Electronic Journal of Differential Equations,2008 (20):359-370. [17]KELEVEDJIEV P S,TERSIAN S A.The barrier strip technique for a boundary value problem withp-Laplacian[J].Electronic Journal of Differential Equations,2013(28):291-331. [18]DAI G W,MA R Y.Unilateral global bifurcation phenomena and nodal solutions forp-Laplacian[J].Journal of Differential Equations,2012,252(3):2448-2468. [19]BEREANU C,GHEORGHE D,ZAMORA M.Non-resonant boundary value problems with singular φ-Laplacian operators[J].Nonlinear Differential Equations and Applications,2013,20(3):1365-1377. [ 20]马如云.非线性常微分方程非局部问题[M].北京:科学出版社,2004.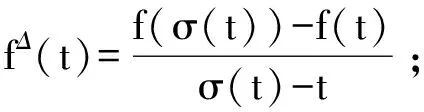
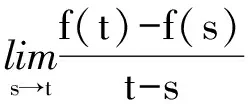
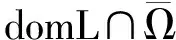
2 主要结果



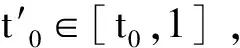
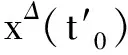
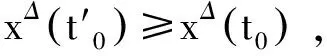

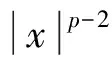
3 例子