连续正奇异线性系统正性判定的一种新方法
,, (山东科技大学 数学与系统科学学院,山东 青岛 266590)
奇异系统,又被称为广义系统、隐式系统、微分-代数系统或半状态系统,是一类由微分及代数方程综合描述的系统,广泛应用于Leontief经济模型[1]、神经网络模型[2]和纽曼模型[3]等实际系统中。近年来,由于自然界中许多模型可以用正奇异系统(状态变量为非负的奇异系统)来描述,如人口模型、电费管理模型、液体体积模型等,正奇异系统引起了学者们的广泛关注。文献[4-12]对正系统的基本问题进行了充分的研究,如可控性、客观性、可达性等。相比较而言,学者们对正奇异系统的研究较晚,包括连续正奇异系统和离散正奇异系统在内的主要研究成果见文献[13-19]。在正奇异系统的正性分析中,文献[13]主要给出了分析离散正奇异系统正性和可达性的充要条件;文献[14-15]通过分析广义Lyapunov方程解的半正定性给出了在离散时间和连续时间状态下刻画正奇异系统正性和稳定性的充要条件;文献[16]在没有不必要的先验条件下,给出了判断连续正奇异系统正性和稳定性的充要条件,并首先提出了用线性规划方法来分析系统的正性和稳定性;文献[17]在没有不必要假设的前提条件下,给出了分析离散正奇异系统正性和稳定性的充要条件,以及基于线性规划的数值算法;文献[18-19]给出了离散正奇异系统存在一个状态反馈,使闭环系统是非负的、稳定的、正则的条件。基于上述研究基础,给出了一种新的刻画连续正奇异系统正性的线性规划方法,该方法没有不必要的先验条件,理论上简单易懂,可行性好,结果清晰明了,能提高系统正性分析的效率。
文中符号的具体说明如下:Rn表示n维实向量空间,Rn×n表示n×n维实矩阵的集合,C表示复数集,Cm×n表示m×n维复数矩阵的集合,AD表示矩阵A的Drazin逆,A-1表示矩阵A的逆,A>0(≥0)表示矩阵A的所有元素aij是正的(非负的),AT表示矩阵A的转置,rank(A)表示矩阵A的秩,I表示单位矩阵,vec(A)表示矩阵A的拉直算子,im(P)表示矩阵P的逆像。
1 简介
考虑时不变齐次奇异系统:
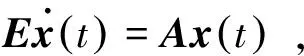
(1)
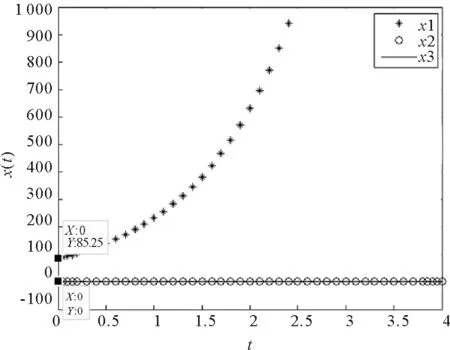
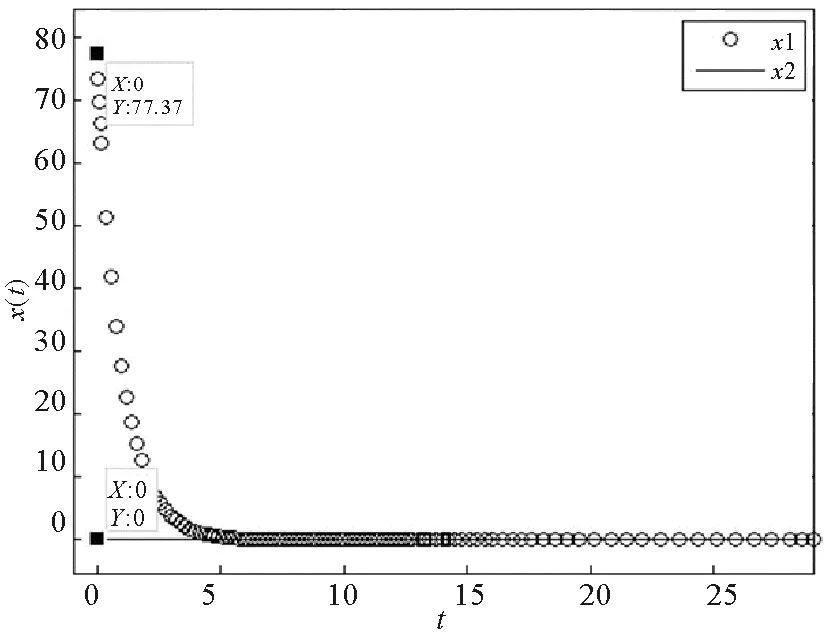
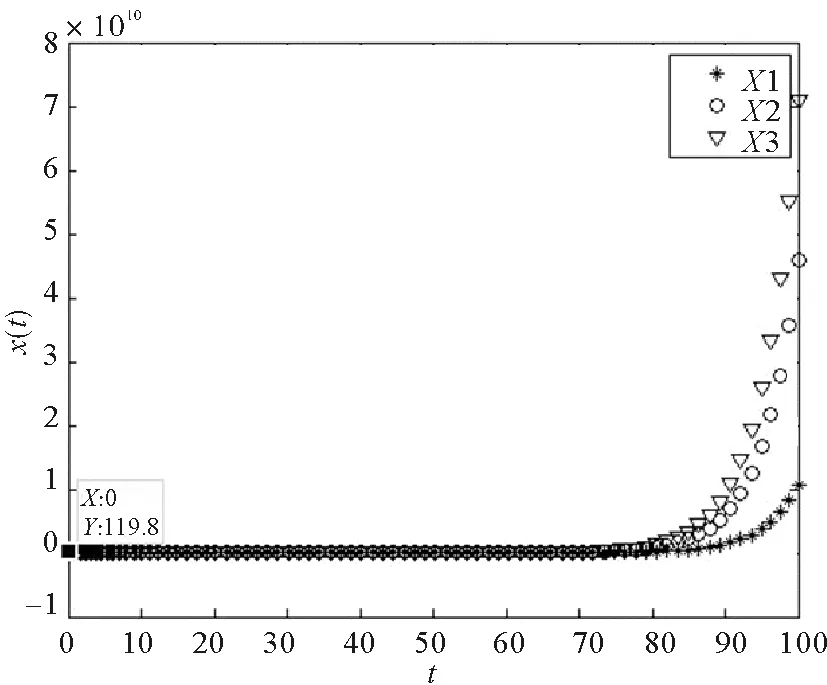
其中E,A∈Rn×n为系统状态矩阵,x(t)∈Rn为系统状态向量,rank(E) 定义1.1[20]设A∈Rn×n且ind(A)=k,存在唯一矩阵X∈Rn×n,满足 AX=XA,XAX=X,XAk+1=Ak。 其中k表示使rank(Ak)=rank(Ak+1)成立的最小非负整数,则X是A的Drazin逆,记作AD。 根据文献[21],任意矩阵A都可化为下列Jordan标准型: (2) 其中,M为可逆矩阵,N为幂零矩阵。则矩阵A的Drazin逆可表示为: (3) 定义1.2[15]E,A∈Rn×n,存在λ∈C,使得det(λE-A)≠0,则称矩阵对(E,A)是正则的。 定理1.3[17] 如果(E,A)是正则的,则系统(1)的解可表示为: (4) 1)P是幂等矩阵(例P2=P); 3) 对于系统(1)的任意解x(t),有Px(t)=x(t)成立。 推论1.5根据定理1.3可知,系统(1)和系统(5)是等价的。 (5) x(0)∈im(P)。 定理1.6[22]考虑方程组AXB=D,设矩阵A∈Cm×n,B∈Cs×r,D∈Cm×r,未知矩阵X∈Cn×s,则vec(D)=vec(AXB)=(BT⊗A)vec(X)。 定义2.1[16]如果对于给定的任意非负可容许初始条件x(0)≥0,有x(t)≥0(t≥0),则称系统(5)是正系统。 定义2.2[23]A=[aij]∈Rn×n,若aij≥0(i≠j),则矩阵A是Metzler矩阵。 定理2.3用A=[aij]∈Rn×n表示n×n维的实矩阵,用M=[mp,q]∈Rn2×n2表示n2×n2维的实矩阵。定义M矩阵: M={mp,q|p≠q:mp,q=0.p=q:m1+(n+1)(j-1),1+(n+1)(j-1)=0,mi+n(j-1),i+n(j-1)=1(i≠j).} 其中,i,j∈[1,2,…,n],p,q∈[1,2,…,n2]。若矩阵A满足M×vec(A)≥0,则A为Metzler矩阵。 注:当A=[aij]∈R1×1时,A不存在非对角线元素,不予考虑。 例如,当矩阵A的维数为2时:i,j∈[1,2],p,q∈[1,2,3,4]。则M∈R4×4,由不等式组M×vec(A)≥0,即 可得a2≥0,a3≥0,即矩阵A的非对角线元素非负。由定义2.2可知,矩阵A为Metzler矩阵。 当矩阵A的维数为3时:i,j∈[1,2,3],p,q∈[1,2,…,9]。则M∈R9×9,由不等式组M×vec(A)≥0可得 由此,a2≥0,a3≥0,a4≥0,a6≥0,a7≥0,a8≥0,即矩阵A的非对角线元素非负。由定义2.2可知,矩阵A为Metzler矩阵。 证明:充分性:A=[aij]∈Rn×n,M=[mp,q]∈Rn2×n2。根据定义2.2可知,判断矩阵是否为Metzler矩阵,只需分析其非对角线元素即可。而向量vec(A)的第i+n(j-1)(其中i≠j)个元素即为矩阵A的非对角线元素,只需左乘一个第i+n(j-1)(其中i≠j)个元素为1的单位行向量mi+n(j-1),使mi+n(j-1)·vec(A)≥0成立,则有矩阵A为Metzler矩阵。 必要性:根据上文分析,若矩阵A为Metzler矩阵,则有mi+n(j-1).vec(A)≥0成立,即M×vec(A)≥0。 根据正奇异系统的解的表达式、正系统的定义以及引理2.5,有下列结论成立。 证明:充分性:令x(0)=Pv0,由定理1.3可得 [x(0)=Pv0=Ps(0)≥0]⟹[x(t)=Ps(t)≥0,∀t≥0]。 定理2.7定义矩阵M=[mp,q]∈Rn2×n2, M={mp,q|p≠q:mp,q=0.p=q:m1+(n+1)(j-1),1+(n+1)(j-1)=0,mi+n(j-1),i+n(j-1)=1(i≠j).} 其中,i,j∈[1,2,…,n],p,q∈[1,2,…,n2],n为系统状态矩阵的维数。 (6) (7) (8) (9) (10) (I) 证明(8)、(9)式成立。 (i) 将矩阵方程组的求解问题转化为线性方程组的求解问题。 Dx=b。 (11) 的求解问题。其中, (ii) 将方程组(11)的求解问题转化为线性规划问题 (7) (iii) 证明上述事实(ii) (12) 接下来用反证法证明x0是方程组(11)的解。假设存在向量x*是方程组(11)的解,则有s(x*) (13) (14) 这与y0是线性规划(7)、(8)和(9)的解相矛盾。 最后证明等式(15)成立。 (15) 类似地,又可证得 (Ⅱ) 证明(10)式成立。 式(10)可转化为M×vec(H)≥0的形式。由定理2.3可得,若矩阵A满足M×vec(A)≥0,则A为Metzler矩阵。 至此,命题得证。 例1[16]考虑具有如下参数矩阵的时不变齐次正奇异系统 根据定理2.7可得, (16) 由MATLAB中的Linprog函数可得: 例2[16]考虑具有如下参数矩阵的时不变齐次正奇异系统 根据定理2.7可得, (17) 图1 例1系统状态轨线图Fig.1 The trajectory of states about example 1 图2 例2系统状态轨线图Fig.2 The trajectory of states about example 2 例3[16]考虑具有如下参数矩阵的时不变齐次正奇异系统 根据定理2.7可得, (18) 由Linprog函数可求得: 例4[16]考虑具有如下参数矩阵的时不变齐次正奇异系统 根据定理2.7可得, (19) 由Linprog函数可求得: 图3 例3状态轨线图Fig.3 the trajectory of states 图4 例4状态轨线图Fig.4 the trajectory of states 主要研究了连续正奇异系统的正性的判定方法。一方面利用Metzler矩阵的非负性约束给出了判断Metzler矩阵的充要条件,另一方面在文献[16]的基础上结合Drazin逆和矩阵拉直算子的相关性质,利用最小绝对差给出了一种新的判定连续正奇异系统正性的线性规划方法。同传统方法相比,该方法简单且易于数值实验,数值实验表明,上述理论方法是正确可行的,在降低理论复杂度的同时,提高了系统正性分析的效率。 参考文献: [2]荣莉莉,张荣.基于离散Hopfiedle神经网络的突发事件连锁反应路径推演模型[J].大连理工大学学报,2013,53(4):607-614. RONG Lili,ZHANG Rong.An exmergency event chain reaction path deduction model based on discrete Hopfield neural network[J].Journal of Dalian University of Technology,2013,53(4):607-614. [3]LUENBERGER D.Dynamic equations in descriptor form[J].IEEE Transactions on Automatic Control,1977,22(3):312-321. [4]OHTA Y,MAEDA H,KODAMA S.Reachability,observability,and realizability of continuous-time positive systems[J].SIAM Journal on Control and Optimization,1984,22(2):171-180. [5]COXSON P G,SHAPIRO H.Positive input reachability and controllability of positive systems[J].Linear Algebra and its Applications,1987,94:35-53. [6]VALCHER M E.Controllability and reachability criteria for discrete time positive systems[J].International Journal of Control,1996,65(3):511-536. [7]FARINA L,RINALDI S.Positive Linear Systems:Theory and Applications[M].New York:John Wiley & Sons,2000. [8]RAMI M A,TADEO F.Positive observation problem for linear discrete positive systems[C]∥2006 45th IEEE Conference on Decision and Control:2006:4729-4733. [9]RAMI M A,TADEO F,Benzaouia A.Control of constrained positive discrete systems[C]∥2007 IEEE American Control Conference,2007:5851-5856. [10]KACZOREK T.Fractional positive continuous-time linear systems and their reachability[J].International Journal of Applied Mathematics and Computer Science,2008,18(2):223-228. [11]LIU X,WANG L,YU W,et al.Constrained control of positive discrete-time systems with delays[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2008,55(2):193-197. [12]LIU X,DANG C.Stability analysis of positive switched linear systems with delays[J].IEEE Transactions on Automatic Control,2011,56(7):1684-1690. [13]BRU R,COLL C,SANCHEZ E.About positively discrete-time singular systems[J].System and Control:Theory and Applications,World Scientific and Engineering Society,Athens,2000:44-48. [14]VIRNIK E.Analysis of positive descriptor systems:topiucs in systems and control theory[M].VDM Verlag, 2008. [15]VIRNIK E.Stability analysis of positive descriptor systems[J].Linear Algebra and Its Applications,2008,429(10):2640-2659. [16]RAMI M A,NAPP D.Characterization and stability of autonomous positive descriptor systems[J].IEEE Transactions on Automatic Control,2012,57(10):2668-2673. [17]RAMI M A,NAPP D.Positivity of discrete singular systems and their stability:An LP-based approach[J].Automatica,2014,50(1):84-91. [18]HERRERO A,RAM A,THOME N.Nonnegativity,stability,and regularization of discrete-time descriptor systems[J].Linear Algebra and its Applications,2010,432(4):837-846. [19]NAPP D,TADEO F,CHAABANE M.State feedback positive stabilization of discrete descriptor systems[J].International Journal of Innovative Computing,Information and Control,2014,10(5):1853-1859. [20]CAMPBELL S L,MEYER,JR C D,Rose N J.Applications of the Drazin inverse to linear systems of differential equations with singular constant coefficients[J].SIAM Journal on Applied Mathematics,1976,31(3):411-425. [21]BEN-ISRAEL A,GREVILLE T N E.Generalized inverses:theory and applications[M].Dordrecht:Springer Science & Business Media,2003:163-164. [22]张贤达.矩阵分析与应用[M].2版.北京:清华大学出版社有限公司,2004:74-77. [23]LUENBERGER D G D G.Introduction to dynamic systems: Theory,models,and applications[R].Palo Alto:Stanford University,1979:204-206.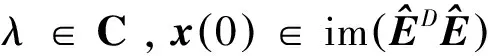
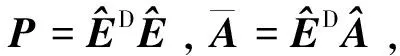
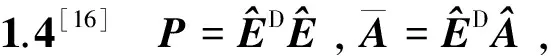
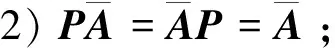
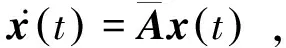
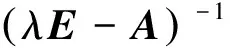
2 正性分析
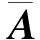
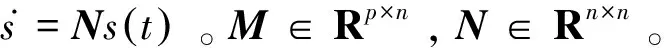
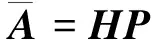
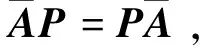
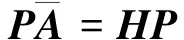
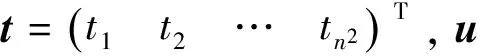
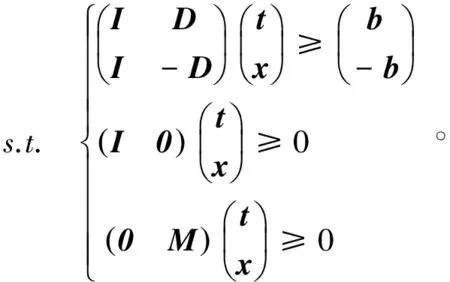
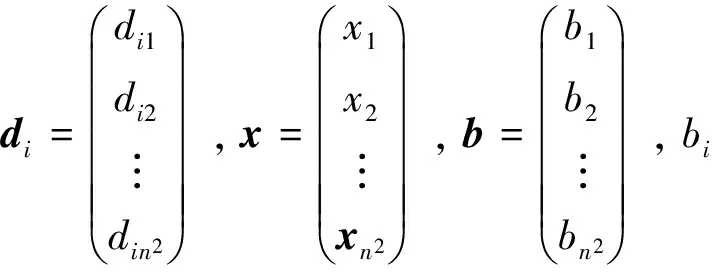
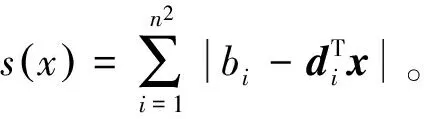

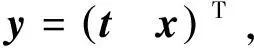
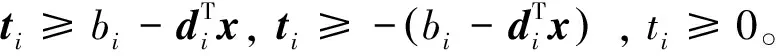
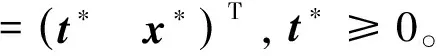
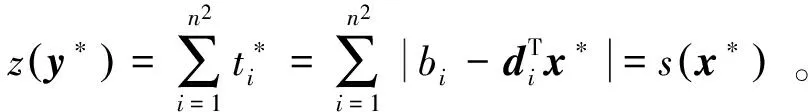
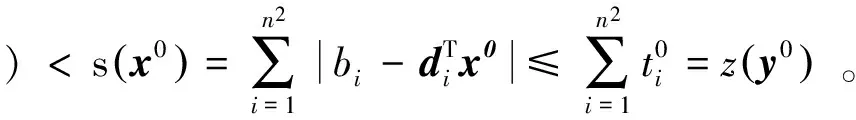
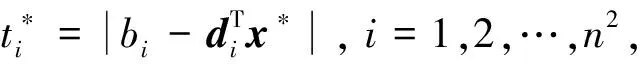
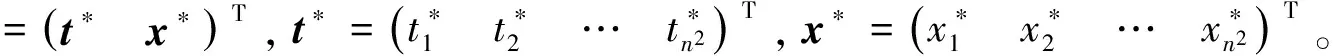
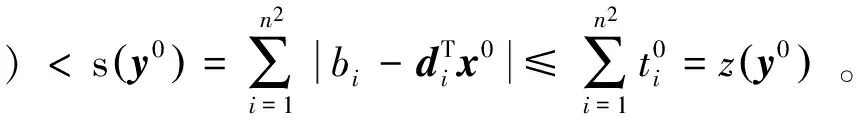
3 数值例子
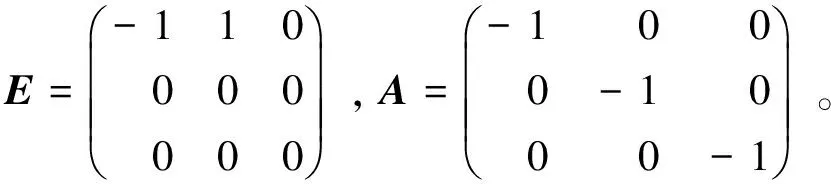
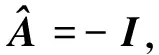

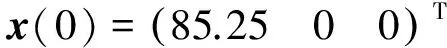
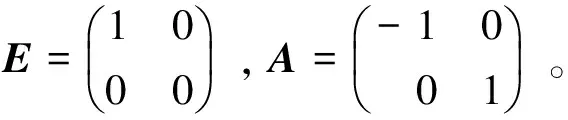
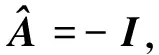
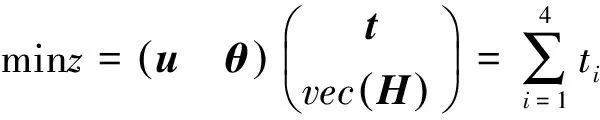

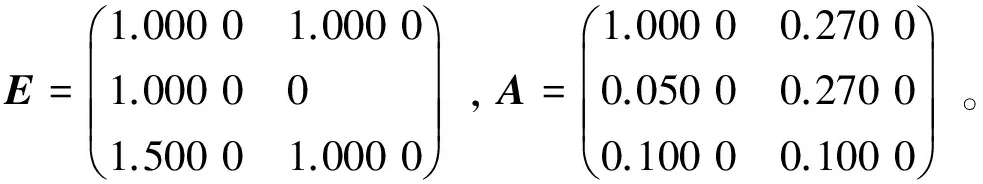
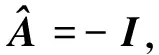
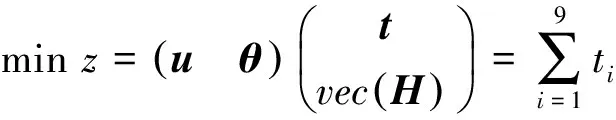

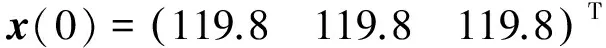
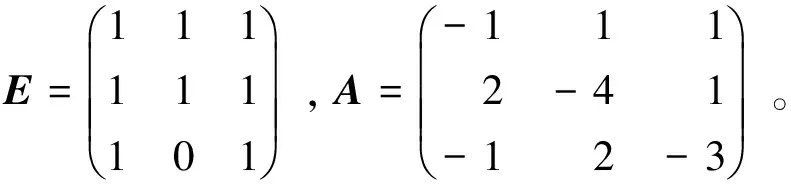
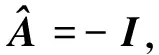
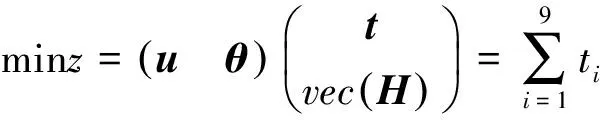

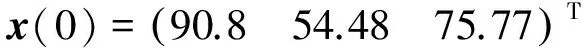
4 结论

