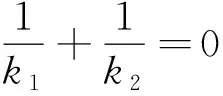抛物线顶点三角形的一个斜率性质

湖北省阳新县高级中学

邹生书 (邮编：435200)

题目已知不过坐标原点O的直线交抛物线y2=2px于A、B两点，若直线OA、AB的斜率分别为2和6，则直线OB的斜率为( )

A.3 B.2 C.-2 D.-3

这是武汉市2018届高中毕业生二月调研测试理科第6题文科第7题，本题不仅“小巧活宽易”，而且平中透奇.笔者通过对本题提出问题、探究问题、最终解决问题，得出了经过抛物线顶点的内接三角形三边斜率的一个有趣性质.下面将本题解法、推广探究、有关结论和多种解法整理成文与读者交流.

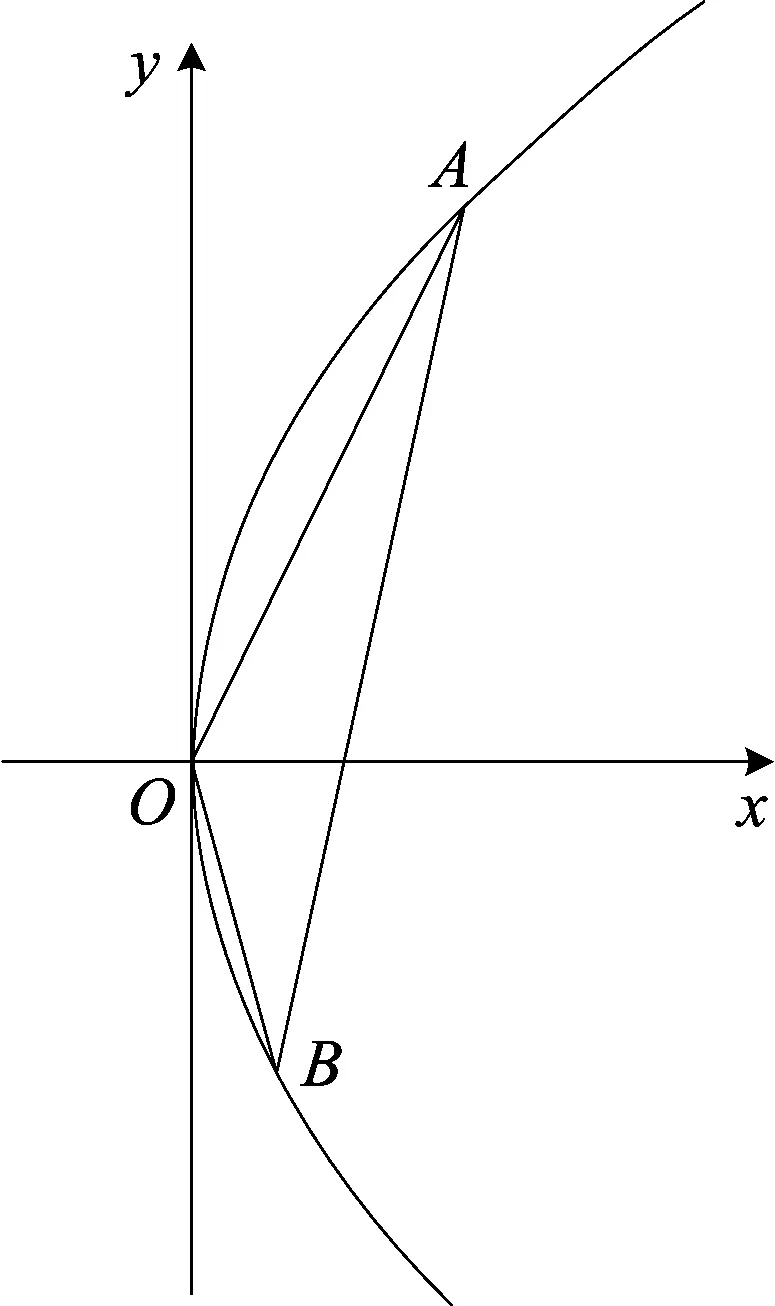
图1

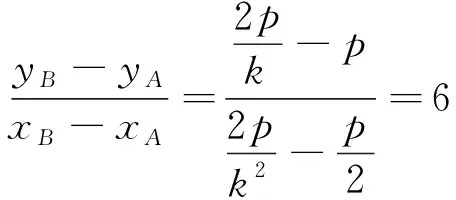
解法2(间接法)依题意根据斜率的几何意义画出大致图象如图1所示.设直线OB的斜率为k,由图知k<0,否定选项A、B.若k=-2,

则OB与OA关x轴对称，直线AB垂直于x轴斜率不存在，故否定选项C，于是应选D.

另解由图可知k<0且k>kOA即-k>2,则k<-2,故选D.

反思这里△OAB的三个顶点都在抛物线y2=2px上且O为抛物线顶点，我们称这个三角形为抛物线的顶点三角形.这道调考题是有关抛物线顶点三角形三边斜率的问题，由图知直线OA、OB的斜率存在且不为零，当直线AB的斜率存在时我们提出如下问题：抛物线的任意一个顶点三角形三边的斜率否存在某种确定的数量关系？这个数量关系是什么？

问题探究已知A,B是抛物线y2=2px上不同于顶点O的任意两点，若直线OA、OB、AB的斜率分别为k1、k2、k3,探究k1、k2、k3是否存在某种关系？

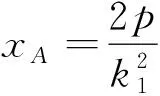
于是我们可得抛物线顶点三角形的三边的斜率有如下性质.

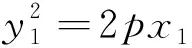
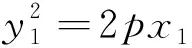
下同法2略.

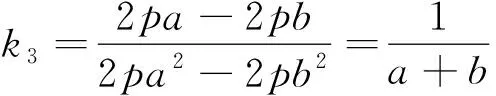
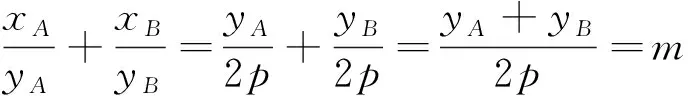
解法6因为直线OA不会与x轴平行，故可设其方程为x=m1y,与抛物线方程y2=2px联立解得yA=2pm1,

.同理设直线OB的方程x=m2y,可得yB=2pm2,

.

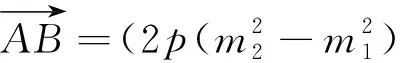
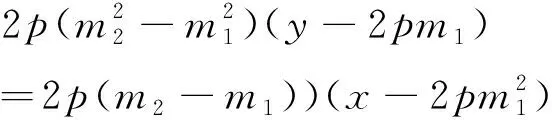
由此可得抛物线顶点三角形如下更一般性结论.

性质2若抛物线y2=2px的顶点△OAB的三边OA、OB、AB所在的直线方程分别为x=m1y,x=m2y,x=m3y+n,则m3=m1+m2.