从生活中发现，在活动中领悟——评袁颢珈老师的“轴对称图形”一课

云南省昆明市高新技术产业开发区第一小学 明文俊 袁颢珈

教材分析：

《轴对称图形》是义务教育教科书（人教版）小学数学第八册第七单元《图形的运动（二）》第一课时的内容。学生在二年级的时候已经初步感知了生活中关于对称的现象，认识了轴对称图形。加上生活经验的积累，学生对于什么是“轴对称图形”并不陌生。部分学生甚至可以用一些方法来判断图形是否是轴对称的。

相较于二年级注重对轴对称图形的整体感受，此时对学生有了更高的要求。四年级侧重于通过动手画图等活动对轴对称进行再认识,并在活动中发现轴对称图形的特征和性质，即对称点到对称轴的距离相等、对称点连线和对称轴互相垂直。

学生分析：

到了四年级，要求学生具备在活动过程中总结经验的能力，并在活动中发现轴对称图形的性质特征，进一步认识轴对称图形，这就是学生的“潜在发展水平”。教学设计应根据学生的“最近发展区”来确定教学环节，以学生在实际操作中的所做、所见、所感为“扶梯”，引导学生一步步发现轴对称图形的性质特征，完成第一学段向第二学段的过渡。

别出心裁巧设计，落花亦能引课题

教学片段一：情境导入，复习旧知

1.教师向学生分享微信朋友圈赏花的照片，激发学生的学习兴趣。

2.出示桃花矢量图，让学生判断发生了变化的桃花图形（掉落花瓣）是否仍是轴对称图形。

3.揭示课题。

活动作“扶梯”，“爬出”轴对称 “特性”

教学片段二：动手操作，自主探究

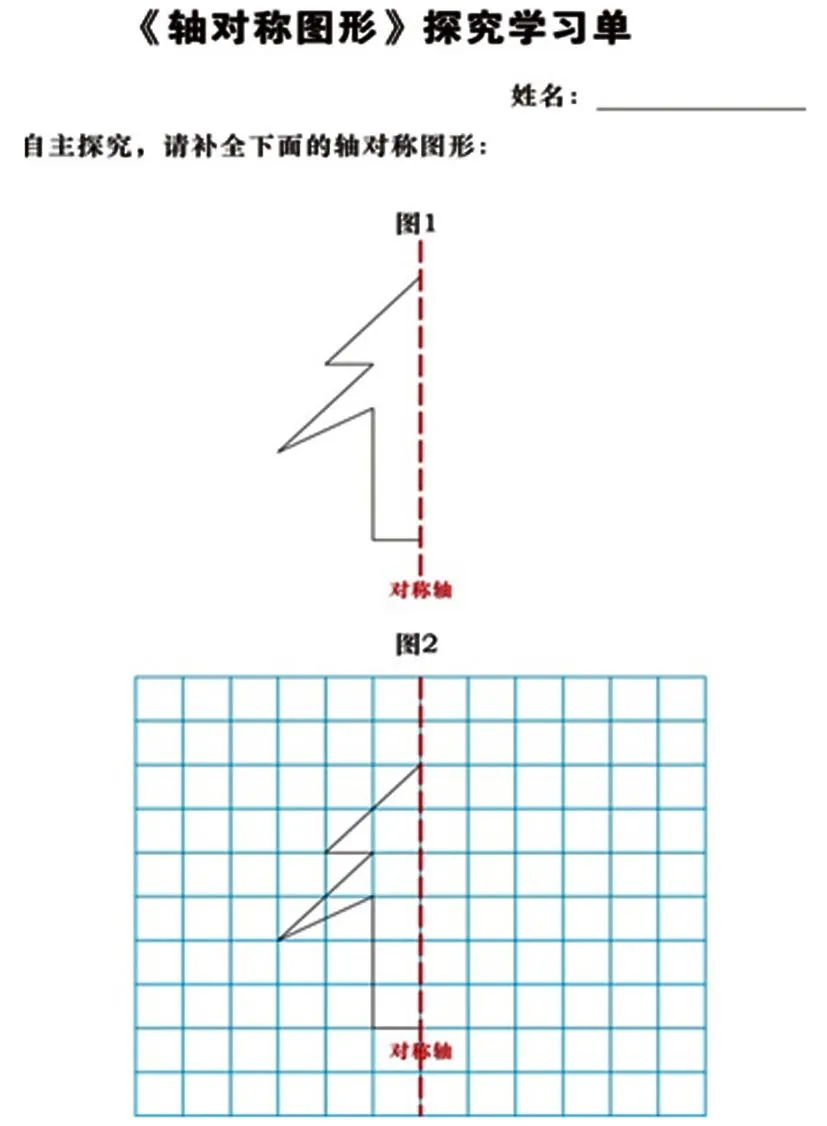
1.学生明确探究活动要求，先自主探究，尝试补全轴对称图形。完成后在四人小组内交流自己的方法。教师加入四人小组听取学生的交流，初步了解学生的方法。

2.教师组织集体汇报交流，突破轴对称图形的性质特征。

（1）紧紧围绕“图形——线段——点”这一核心，突破“对称点到对称轴的距离相等”这一性质特征。

师：用有方格的一面作图的请举手，用没有方格一面作图的请举手。为什么大多数同学更愿意选择用有方格的一面补全轴对称图形？

生：因为有方格对比原图，更容易确定另一边的图形，比较好画。

师：那你能具体说一说是怎么画的吗？

（在实物展台上进行展示，学生边比划边说自己的方法）

师：你画的这一条条的都是这个图形的什么部分？

生：是围成图形的线段。

师：请你着重介绍一下第一条线段的画法。

生：我先找到线段的端点，原图中，这个端点距离对称轴有2格，所以在对称轴另一侧和它对应的点也要距离对称轴2格。我数好了把这个端点画在这里。

师：那如果这个端点不在距离对称轴2格的这个位置，会怎么样呢？

生：就不能和原图中的点重合，就不是对称的了。

师：（顺势总结）在轴对称图形中，沿对称轴对折，左右两侧能重合的两个点叫做对称点。为了能一眼看出来它们是一对对称点，我们用字母A和A’来表示。刚才这位小老师就是通过找原图中线段端点的对称点，画出第一条线段。

（教师鼓励其他同学用同样的方法说一说怎样画第二条、第三条线段，以检测学生是否清楚。通过几位小老师的讲解，学生发现，补全轴对称图形就是要画出围成图形的线段，而线段又是由线段两端的端点确定的，所以找原图线段端点的对称点是解决问题的关键。）

师顺势提问：在找对称点的过程中，你们有什么发现？

生：点A到对称轴是距离是2格，它的对称点到对称轴距离也要是2格，对称的两个点到对称轴距离相等。

师：对称点都是成对出现的，那在对称轴上的这个点，它的对称点在哪？

引导学生观察、思考，发现对称轴上的点的对称点就是它本身。

（2）利用方格纸的横格线、竖格线的直观特点，引导学生观察、思考，并借由原有知识经验“直线外一点到直线的距离”，突破“对称点连线和对称轴互相垂直”这一性质特征。

师：点D到对称轴距离是3格，所以它的对称点D’到对称轴距离也要是3格，可是距离对称轴是3格的点很多，为什么点D’一定要在这？

生：因为若点D和D’要重合，就要在同一条直线上。

师：你能用红笔表示出是哪一条直线吗？

（学生将D和D’连接起来。）

师：请大家仔细观察，D和D’的这条连线和对称轴是什么位置关系？

生：是互相垂直的。

师：真的如我们眼睛所看到的互相垂直吗？点D是对称轴外的一点，对称轴是一条直线。直线外一点到这条直线的距离是指“过直线外一点画这条直线的垂线”，所以点D到对称轴的这条线段和对称轴是互相垂直的，以此类推，D’到对称轴的线段和对称轴也是互相垂直的，这两条线段在同一直线上，所以DD’的连线和对称轴确实是互相垂直的。那其他对称点也有这个特征吗？

（引导学生一一验证）

师生共同小结：对称点连线和对称轴互相垂直。

（3）请没有方格纸画图的学生交流方法，再次巩固探究发现的两条性质特征。

（4）师生共同总结，渗透补全轴对称图形的方法。

师：比较有方格和没方格的画图过程，有什么共同的地方？

（学生异口同声都回答是在找对称点）

师：在补全的过程中，都是在找原图中线段端点的对称点，确定了对称点的位置，就能连成线段，从而围成了轴对称图形。

通过以上教学片段的重现和分析，可窥一斑而知全豹，在此笔者有以下感触。

1.学生是学习的主体，教师应结合学生的“实际发展水平”来进行教学设计。

本节课从“回顾——认识——再认识”，教师并没有以“告诉”的形式去灌输，而是创设了一种环境和氛围，让学生在活动中学习，体现了“做中学”的原则。课堂活动中不仅培养了学生的合作意识，还渗透了对应思想。与此同时，教师成功的扮演了“组织者”和“引导者”的角色，调控了整个探究活动，体现了教师为主导，学生为主体的原则。

2.上课时教师勇于“让位”给学生。

教师把“讲堂”变“学堂”，将学习主动权交给学生，在补全轴对称图形时放手让学生去补全，只要学生能自己操作、自己领悟的，都由学生自己完成，教师只是起到引导和点拨的作用。

3.教学应不拘泥于教材，要根据学生的情况及教学需要有效的使用。

教师只有真正认识到自己在教学活动中的角色，并有效的进行转变，才能让学生在学习中得到发展。