非齐性空间上的双线性广义分数次积分算子

郑涛涛，来越富

(浙江科技学院理学院，杭州310023)

在近20年中，经典欧式空间上的调和分析被延拓到非双倍测度空间，其中测度μ仅满足多项式增长条件，即存在正常数C0使得对所有的x∈n及r∈(0，∞)有

B(x，r) ∶={y∈n:|x－y|＜r}。显然，上式中的测度并不满足双倍条件:μ(B(x，2r))≤Cμ(B(x，r))。非双倍测度的分析学在解决长期而又公开的Painlevé问题时起着很重要的作用［1］。2010年，Hytönen［2］引入了一类满足几何双倍与上双倍条件的距离测度空间(X，d，μ)，此空间也称为非齐性空间(见定义2与定义3)。带多项式增长条件的度量空间与带双倍条件的齐性空间很自然地被这类新的距离测度空间所包含。

在这类更广的非齐性空间上，许多人研究了Calderón-Zygmund奇异积分算子的相关性质［3-7］。但是由于空间(X，d，μ)的弱结构，测度在平移和伸缩时性质较差，致使对分数型积分算子在非齐性空间上的研究结论尚不完善。因此，本文将以此非齐性空间(X，d，μ)为底空间来研究双线性广义分数次积分算子。

1 广义分数次积分算子及相关定义

对于经典欧式空间上的分数次积分算子，定义如下

其有著名的 Hardy-Littlewood-Sobolev定理［8］，即对所有的 q∈(1，n/η)，1/p=1/q－η/n，Jη是从 Lq(n)到Lp(n)的有界算子。付星等［9］515在非齐性空间(X，d，μ)上研究了广义分数次积分算子Tβ的有界性与弱型端点估计的等价刻画，其中

但广义分数次积分算子在(X，d，μ)上的(Lq(μ)，Lp(μ))有界性以及弱型端点估计的证明至今还是一个公开的问题。关于广义分数次积分算子的研究，类似于Calderón-Zygmund奇异积分算子，需假定广义分数次积分算子满足某一定的有界性。在此基础上，周疆等［10］8以(X，d，μ)为底空间研究了广义分数次积分算子Tβ在非双倍测度Morrey空间上的有界性。谢如龙等［11］3将广义分数次积分算子推广到双线性情形并研究了其交换子。在文献［10-11］中，为获得广义分数次积分算子的若干有界性，需要对(X，d，μ)中的测度μ加齐次性辅助条件。本文拟以(X，d，μ)为底空间，研究双线性广义分数次积分算子在非双倍测度Morrey空间上(见定义4)的有界性，且关于测度μ不需增加齐次性辅助条件。为陈述本文的主要问题，我们先给出相关定义。

定义1 在(X，d，μ)上的双线性分数次积分算子的定义，设A＞0是一个常数，α∈(0，2)。设K(x，y1，y2)是(X)3的对角线 {x =y1=y2}之外的局部可积函数，并满足下面的尺寸条件与光滑性条件:

1)当(x，y1，y2)∈(X)3且 x 不等于某个 yi(1≤i≤2)时，

假设算子Iα是双线性的，对L∞中的有紧支集的可测函数fi以及几乎处处的xsupp fi若成立下式

则称Iα是以K为核的双线性广义分数次积分算子。

定义2［2］489如果存在数N∈ 使得对任意开球B(x，r)X最多被N个球B(xi，r/2)覆盖，则称空间(X，d)为几何双倍度量空间。

定义3［2］489如果存在控制函数λ:X×+→+以及常数Cλ使得(X，d，μ)中的Borel测度μ满足以下3条件，则称测度μ满足上双倍测度。

1)对任意固定的x∈X，关于半径r→λ(x，r)是递增的。

2)对于所有 x∈X，0＜r＜∞，μ(B(x，r))≤λ(x，r)≤Cλλ(x，r/2)成立。

3)对于所有的半径 r＞0，x，y∈X，若 d(x，y)≤r，则有 λ(x，r)≈λ(y，r)。

定义 4［10，12－13］设 k＞1，1≤q≤p＜∞ ，Morrey 空间可由如下形式给出

其中，

当 1≤s≤t≤p＜∞时，利用 Hölder不等式可得 Lp(μ)=(k，μ)(k，μ)(k，μ)。设k，k珓＞1，有(k，μ)≈(k珓，μ)成立，这说明Morrey空间的定义与常数k，k珓的选取无实质性的关联。下文中将取k=6，并记(6，μ)为(μ)，类似的性质也可参见文献［14-15］。

关于本文常用的一些符号，若p≥1，p'=p/(p－1)表示p的对偶指标，fg表示存在常数 C使得f≤Cg，χE表示可测集E的特征函数。

2 主要结论

假定对于某些 r∈(1，β)，1/s=1/r－β，广义分数次积分算子 Tβ是(Lr(μ)，Ls(μ))有界的。本文将以(X，d，μ)为底空间，测度μ仅满足上双倍条件的基础上，研究双线性广义分数次积分算子Iα在Morrey空间上的有界性。主要结论如下:

定理1 设K为双线性分数次积分核，Iα为式(2)所定义的双线性广义分数次积分算子，α∈(0，2)。设1＜qi≤pi＜∞，fi∈(μ)，i=1，2，且有 1/p=1/p1+1/p2－α，1/q=1/q1+1/q2－α，则存在正常数 C 使得

注:若双线性广义分数次积分算子Iα退化为线性的广义分数次积分算子Tβ，则本文的结论可以包含文献［10］中的部分结论。注意到文献［10-11］中其控制函数λ需增加额外的条件:即“存在t∈(0，∞)使得对所有的x∈X以及a，r∈(0，∞)都有λ(x，ar)=atλ(x，r)”，而在本文的定理证明中λ不需满足此额外条件。

3 主要结论证明

在证明定理1之前，我们先给出一个双线性广义分数次积分算子Iα在乘积Lebesgue空间上的有界性命题以及一个引理，这对于证明Iα在乘积Morrey空间上的有界性起着关键作用。

命题1 设K为双线性分数次积分核，Iα为(2)式所定义的双线性广义分数次积分算子，α∈(0，2)。设 1＜p1，p2＜∞，0＜1/p=1/p1+1/p2－α＜1，fi∈Lpi(μ)，i=1，2，则存在正常数 C 使得

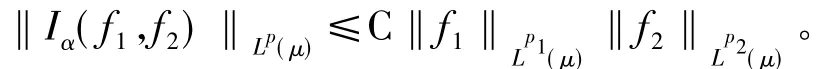
证明:先对双线性广义分数次积分算子Iα做点态估计，

设有 t1，t2∈(1，2/α)使得 1/t1=1/p1－α/2，1/t2=1/p2－α/2。下面需要利用广义分数次积分算子 Tα/2的(Lpi，Lti)有界性来证明Iα的有界性。由于1/p=1/t1+1/t2，利用Hölder不等式得

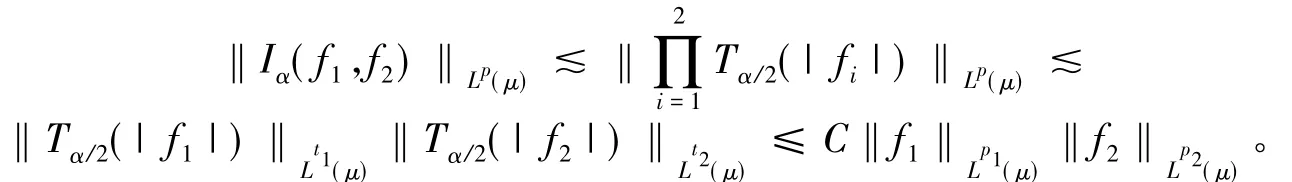
命题1证毕。

引理 1 设 f∈Lq(μ)，0＜β＜1/q＜1 时，有

证明:利用Hölder不等式得

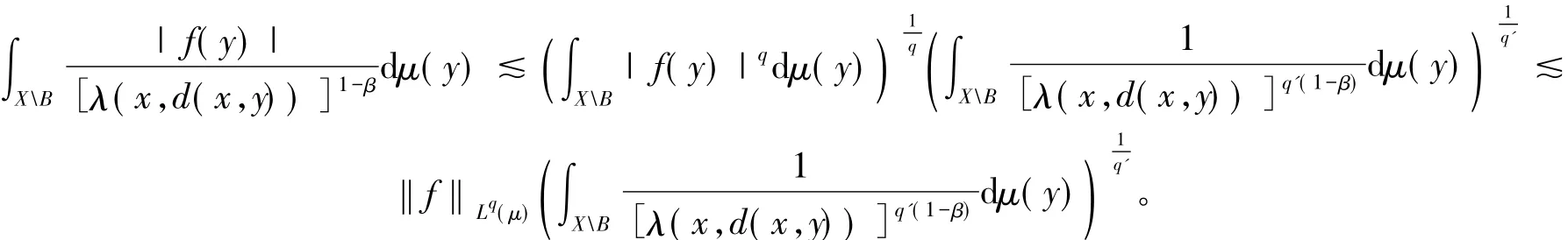
若是能证明下式成立

则因 β ＜1/q，测度 μ(B(x，r))≤λ(x，r)，容易得到引理 1 的结论

下面我们将证明式(3)。首先构造辅助性的半径序列{r0，r1，r2…}使得r0=r，ri+1是满足2kri形式的最小半径，其中 k∈ 且 λ(x，2kri)＞2λ(x，ri)，{Bi}i∈={B(x，ri)}i∈。可得简单的递推关系 2iλ(x，r)≤λ(x，ri)，i∈+，再借助 λ 的性质可以得到

由此可以得到，

引理1证毕。

下面我们给出定理1的证明。固定球B∈X，x∈B，可将函数fi分解为fi=f0i+f∞i，其中f0i=fiX2B，f∞i=f－f0，i=1，2，可得

首先估算E1(x)，利用命题1中Iα的有界性结论，可得

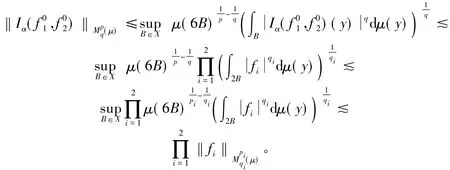
关于 E2(x)，对 α 做分解 α=α1+α2使得 α1＜1/q1，α2＜1/q2。利用核 K 的尺寸条件式(1)以及对所有的 x，y∈X 且 d(x，y)≤r有 λ(y，r)≈λ(x，r)，

根据上面的估计式有

由于E2(x)与E3( x )具有对称性，类似地可以得到E3( x)的估计

对于第一项E41(x)，利用广义分数次积分算子核的尺寸条件式(1)，可得

由此可得 E41(x)与 E42(x)都可以被1/p=1/p1+1/p2－α，1/q=1/q1+1/q2－α，利用引理 1 中的结论可得

结合E41(x)与E42(x)以及上面的估计式，可得

综合E1(x)，E2(x)，E3(x)，E4(x)的估计式可得定理1的结论。定理1证毕。

4 结论

通过对函数的分解，将积分区域进行环状分割，可将双线性广义分数次积分算子在乘积Lebesgue空间上的有界性以及在Morrey空间上的有界性，转化为线性情形的有界性来处理。

［1］ TOLSA X.Painlevé’s problem and the semiadditivity of analytic capacity［J］.Acta Mathematica，2003，190(1):105.

［2］ HYTNEN T.A framework for non-homogeneous analysis on metric spaces，and the RBMO spaces of Tolsa［J］.Publicacions Matematiques，2010，54(2):485.

［3］ HU G，MENG Y，YANG D C.Weighted norm inequalities for multilinear Calderón-Zygmund operators on non-homogeneous metric measure spaces［J］.Forum Mathematicum，2014，26(5):1289.

［4］ LIN H B，WU SQ，YAND D C.Boundedness of certain commutators over non-homogeneous metric measure spaces［J］.Analysis and Mathematical Physics，2017，7(2):187.

［5］ ZHENG T T，WU X M，TAO X X.Bilinear Calderón-Zygmund operators of type ω(t)on non-homogeneous space［J］.Journal of Inequalities and Applications，2014(1):113.

［6］ ZHENG T T，WANG Z，XIAO W.Maximal bilinear Calderón-Zygmund operators of typeω(t)on non-homogeneous space［J］.Annals of Functional Analysis，2015，6(4):134.

［7］ ZHENG T T，TAO X X.Boundedness for iterated commutators of multilinear singular integrals of Dini’s type on nonhomogeneous metric measure spaces(in Chinese)［J］.Science sinica mathematica，2017，47(9):1029.

［8］ CHEN J C，FAN D S，ZHENG T T.Estimates of fractional integral operator with variable kernel［J］.Publicationes Mathematicae Debrecen，2017，90(1):39.

［9］ FU X，YANGDC，YUAN W.Generalized fractional integrals and their commutators over non-homogeneous metric measure spaces［J］.Taiwanese Journal of Mathematics，2014，18(2):509.

［10］ CAO Y H，ZHOU J.Morrey spaces for non-homogeneous metric measure spaces［J］.Abstract and Applied Analysis，2013(4):1.

［11］ GONG H J，XIE R L，CHEN X.Multilinear fractional integral operators on Non-homogeneous metric measure spaces［J］.Journal of Inequalities and Applications，2016(1):1.

［12］ TAO X X，ZHENG T T.Multilinear commutators of fractional integrals over Morrey spaces with non-doubling measures［J］.Nonlinear Differential Equations and Applications，2011，18(3):287.

［13］ KOMORI-FURUYA Y，SATO E.Weighted estimates for fractional integral operators on central Morrey spaces［J］.Mathematische Nachrichten，2017，20(3):2901.

［14］ YAN Y，CHEN J，LIN H B.Weighted Morrey spaces on non-homogeneous metric measure spaces［J］.Journal of Mathematical Analysis and Applications，2017，452(1):335.

［15］ 郑涛涛，张松艳.一类算子在非倍测度的广义Morrey空间上的有界性［J］.浙江科技学院学报，2011，23(1):1.