轮盘超椭圆异型螺栓孔均衡优化设计
韩佳欣,郭海丁
(南京航空航天大学江苏省航空动力重点实验室,南京210016)
0 引言
航空发动机实际服役情况和试验表明,高转速下的发动机轮盘的孔结构极易出现应力集中,导致整体结构强度储备降低[1-2]。对于发动机盘类部件的螺栓连接而言,螺栓通孔在交变应力作用下容易产生疲劳裂纹并扩展到附近的承力结构,最终导致整个结构失效[3]。因此,降低孔边应力集中并提高轮盘乃至整个发动机的寿命,是提高发动机安全性和可靠性亟需解决的关键问题[4-5]。解决孔边应力集中问题的传统措施有孔边倒角、抛光以及改变结构尺寸等,但这些常规方法降低应力的效果并不明显,甚至会增加结构质量[6]。针对此类问题,美国GE公司和法国SNECMA公司联合研制的CFM56-Ⅲ型航空涡轮发动机将位于高压涡轮盘前安装边的螺栓孔改进为1种8圆弧连接异型螺栓孔,并于1984年通过适航认证。这一反传统结构引起了中国航空发动机学者的关注。对其孔边受力特性的研究表明,这种异型孔可以有效降低螺栓孔附近应力的大小,改善应力的分布情况,从而提高发动机的寿命[7-8]。然而,8圆弧异型孔轮廓设计参量较多,优化模型也略显复杂,而且由于采用异型孔会导致孔轮廓尺寸增大,给连接结构的传力带来负面影响。
为克服上述缺点,本文基于超椭圆曲线引入1种数学模型更为简洁的异型孔结构方案对轮盘螺栓孔进行优化,通过引入超椭圆孔轮廓异型度,对优化过程中的孔轮廓尺寸变化幅度进行控制。此外,对最优解附近设计变量灵敏度进行了分析。
1 超椭圆孔轮廓特征及分析
1.1 超椭圆孔及轮廓异型度的定义
自1812年Adolph Göpel首次提出以来,超椭圆方程已经演变出多种形式,并且在不同领域得到广泛应用,如密码学、数学、宇宙学和工程领域等[9-11]。其最常见的1种形式为
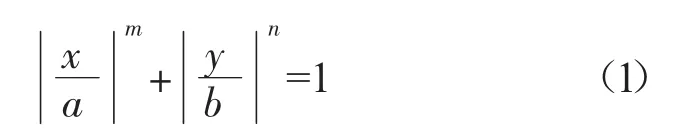
式中:a、b为超椭圆半轴长,主要限制超椭圆孔大小;m、n为形状指数,决定超椭圆形状。
为保证超椭圆轮廓光滑连接,超椭圆指数取值均大于2。m、n取值不同时得到的超椭圆螺栓孔轮廓形状如图1所示。

图1 超椭圆曲线几何形状(m,n>2)
研究表明,随着指数m、n的增大,孔边最大应力有明显下降,但得到的超椭圆孔轮廓可能接近方孔,孔轮廓面积也相应增大,这会明显减少连接面接触面积。对于类似的螺栓连接结构,螺栓孔轮廓面积的增大会加剧预紧力损失,减小连接结构抗滑移系数,进而降低结构抗剪承载能力,最终影响连接单元间的传力传扭[12-14]。
为比较超椭圆孔与原螺栓孔(基圆)的面积变化,本文引入超椭圆异型度Rs

式中:Sc为基圆面积;Sh为超椭圆孔轮廓面积。当0≤x≤a,0≤y≤b 时,式(1)可变形为

基圆面积Sc可按圆形面积公式求得

式中:r为优化前圆形螺栓孔半径。
而Sh的求解为

对该式做数值积分可得

式中:h=a/p;a、b为超椭圆半轴长,为方便装配,设定异型孔轮廓与基圆在x,y轴相切,即a=b=r;Sc始终小于Sh;p为积分区间内采样点数;h为计算精度,一般设为0.001。
a、b确定时,超椭圆孔异型度只与指数m、n有关。超椭圆异型度随m、n的变化关系如图2所示。
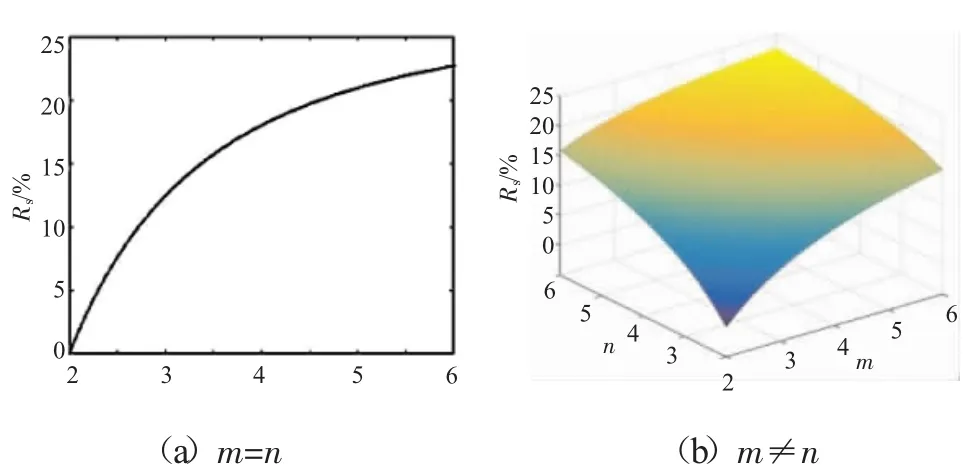
图2 超椭圆孔异型度随指数m、n的变化关系
从图中可见,随着指数m、n的增大,超椭圆孔异型度逐渐增大,当指数大于6时,异型度甚至超过25%(图1(b)),这无疑会阻碍结构间的可靠传力和传扭。
1.2 涡轮盘超椭圆孔异型度设计分析
某航空发动机轮盘连接单元由1根长螺栓将前鼓筒轴、封严盘和涡轮盘装配在一起,如图3所示。其中涡轮盘前安装边通过托板自锁螺母与螺栓配合,连接结构的剖面如图4所示[15]。
采用异型螺栓通孔结构时,降低孔边应力当然是主要目标,但还需要注意由于孔轮廓的改变(即异型度变化)对螺栓连接结构传力可靠性的影响。对于图3中的轮盘螺栓连接结构,涡轮盘螺栓孔面积增大会导致涡轮盘前安装边与托板螺母的接触面积(即图4中的接触面B)减小,轮盘端面上螺栓孔周围产生高压应力,使得孔边被压平磨光,因此会降低螺栓结构的抗滑移承载能力,影响结构传力和传扭[13]。此外,异型度较大的螺栓孔更加接近方孔,给加工和装配带来困难。

图3 轮盘连接结构

图4 轮盘螺栓连接单元
因此,采用超椭圆异型螺栓孔时,在追求应力降低的同时,应尽量保持孔轮廓异型度较小。这也使得设计更稳健,有利于提高结构的可靠性和降低加工装配的难度。
2 涡轮盘超椭圆螺栓孔均衡优化设计方法
2.1 多目标超椭圆异型螺栓孔均衡优化模型
在设计变量变化范围内,异型孔孔边应力随孔轮廓异型度的增大而降低[5]。优化时,单一寻求更低的孔边应力,可能会导致螺栓孔异型度过大,从而导致装配精度降低、加工难度增大,进而使传力的可靠性降低。为此,本文提出1个多目标均衡优化模型,该优化模型包括2个互斥的单目标函数,借以均衡考虑超椭圆螺栓孔异型度减小与孔边应力降低2个互相制约的优化目标。在有效降低孔边应力至设定值的同时,保证超椭圆孔具有恰当的异型度,从而保证结构的可靠传力。其具体形式为
优化目标:

约束:

式中:Mup.、Mlow.和 Nup.、Nlow.分别为 m、n 的上下取值边界;σmax为孔边最大第1主应力。
优化目标由2个互斥的目标函数f1(σmax)和f2(m,n)组成,Rs见式(2),Rσ为孔边应力降低率

式中:σr为原螺栓孔孔边最大应力。
2.2 某涡轮盘超椭圆螺栓孔均衡优化
考虑到超椭圆异型螺栓孔多目标均衡优化模型的目标函数与设计变量成复杂的非线性关系,采用经典的多目标优化方法NSGA-Ⅱ对其进行寻优。该方法基于Pareto非劣占优原理,得到的Pareto前沿(即非劣最优解组成的集合)分布均匀,适用于求解适应度函数复杂的多目标优化问题[16-18]。
对于某型涡轮连接结构(图3、4),其正常工作时涡轮盘前安装边受到多种因素影响,如离心力、扭矩、预紧力、轴向载荷、径向温度梯度和过盈配合产生的载荷等。为兼顾优化模型高效且易行,须对载荷进行简化。涡轮盘螺栓孔孔边应力水平主要受离心载荷影响,优化时仅考虑轮盘及叶片离心载荷所得到的孔型,即使在复杂载荷模型下也保持其优势,依然为应力最小的孔型[5-7]。
采用文献[5]、[6]所提供的简化力学模型,基于超椭圆孔均衡优化设计方法,对图3中的涡轮盘前安装边上螺栓孔进行优化,步骤如下:
(1)设定优化参数。涡轮盘材料为GH4169;轮盘工作转速ωmax=14731 r/min,工作温度为450℃;超椭圆曲线半轴长 a=b=r(基圆半径);2 mm≤m(n)≤6 mm。
(2)基于轮盘简化力学模型,运用Ansys有限元分析得到孔边第1最大主应力;运用式(2)~(6)计算得到孔轮廓异型度。建立超椭圆螺栓孔多目标均衡优化模型。
(3)运用非劣占优多目标遗传算法(NSGA-Ⅱ)对模型进行Pareto非劣占优评估,得到满足收敛代数和终止准则的Pareto前沿。
(4)分别设定模型中2个优化目标理想优化值
(5)对Pareto前沿的非占优解进行二次挑选,最终获得最接近设计者理想值的最优设计解。优化流程如图5所示。

图5 超椭圆螺栓孔均衡优化方法
3 优化结果与讨论
3.1 超椭圆螺栓孔优化结果
基于均衡优化方法可得单参量(m=n)和双参量(m≠n)时超椭圆螺栓孔多目标均衡优化问题的Pareto前沿,如图6、7所示。
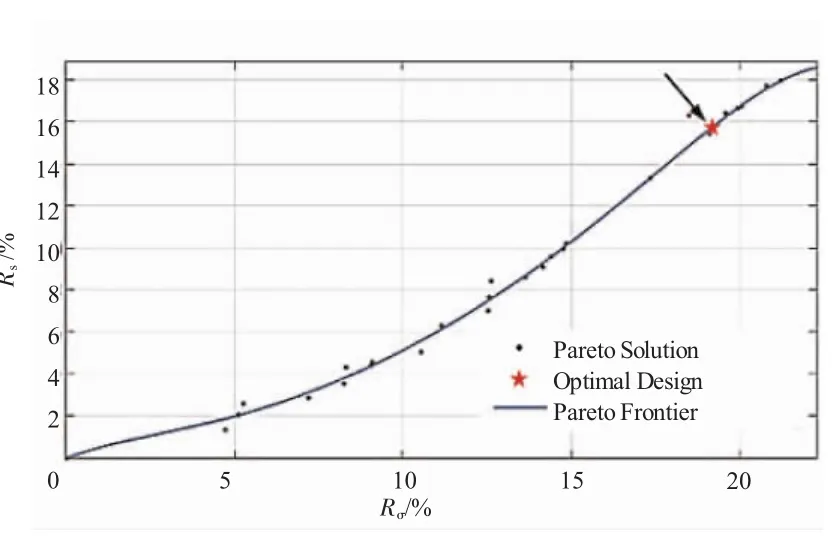
图6 单参量超椭圆孔Pareto前沿(m=n)
图6 、7中Pareto前沿曲线上方的区域为设计可行域,超椭圆孔最优解位置如箭头所示,优化所得设计参数见表1。
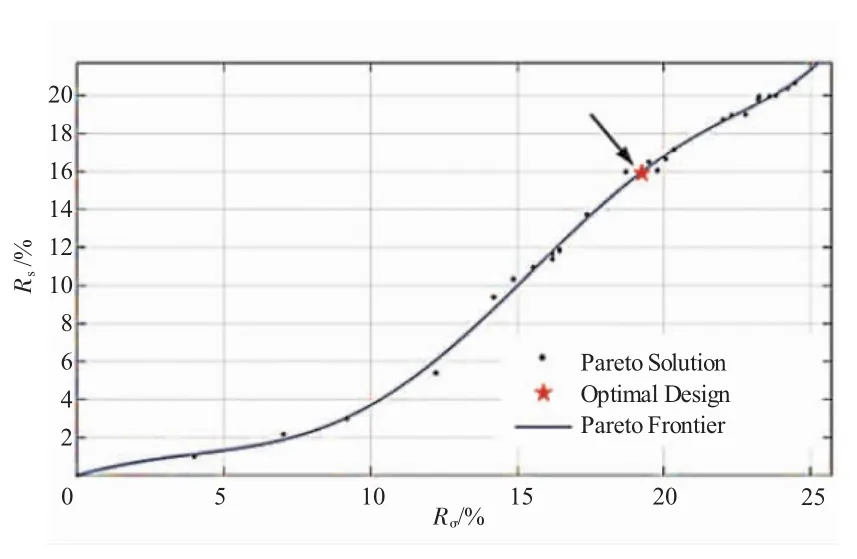
图7 双参量超椭圆孔Pareto前沿(m≠n)

表1 超椭圆孔优化结果
由此可见,本文提出的均衡优化方法可有效地在2个互斥的优化目标间寻得折衷解,在孔边应力下降率达到预期值的同时,使得孔轮廓异型度最小,保证了连接结构的可靠传力。
3.2 异型孔优化模型及优化效率比较
将超椭圆螺栓孔均衡优化模型与文献[19]中提出的8圆弧光滑连接的异型螺栓孔优化模型比较,并通过式(10)求解2种模型的全局搜索能力(GSC)对二者的稳定性进行对比。

式中:N=30,表示重复独立运行2种模型的次数;k为得到全局最优解的次数。
2种优化模型主要区别见表2。

表2 2种异型螺栓孔优化模型对比
经对比可知,8圆弧异型孔降低孔边应力的效果更加明显,而超椭圆螺栓孔均衡优化模型则更加简洁,设计变量数目更少,寻优空间更好把握,优化耗时也明显降低,且优化效果较均衡,具备较好的传力传扭性能。此外,多个优化目标加强了对寻优空间的搜索能力,便于准确定位得到最优解,提高了优化方法的稳定性。2种孔型的轮廓差异的直观对比如图8所示。

图8 不同螺栓孔优化轮廓对比
4 设计稳健性分析
4.1 超椭圆螺栓孔孔边应力响应面
为分析设计变量对孔边应力下降率的影响,分别做单参量和双参量超椭圆孔应力响应面。
(1)单参量超椭圆孔应力响应面如图9所示。

图9 单参量超椭圆孔应力下降率响应面
单参量超椭圆孔指数m增大时,应力下降率先增大后减小;m=4.0~4.5时,孔边应力下降最为明显。运用多项式拟合应力下降率的响应面函数为
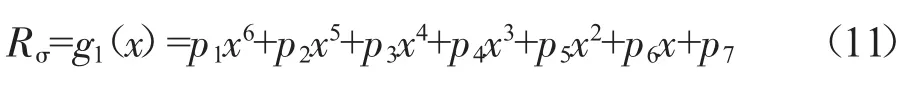
式中:x代表指数m=n;p1~p7为拟合多项式系数,其取值见表3,该情况下拟合的均方根误差RMSE=0.6389。

表3 单参量响应面拟合多项式系数
(2)双参量超椭圆孔应力响应面如图10所示。
从图中可见,孔边应力下降率随指数n的增大而单调增大,随m的增大先增大后减小,当m=3.0~3.8时,达到峰值。同样采用多项式对该响应面进行拟合,得到孔边应力降低率与指数间关系为

式中:x、y分别为指数 m、n;系数 p00~p13的取值见表4,此时均方根误差 RMSE=1.734×10-12。

图10 双参量超椭圆孔应力下降率响应面

表4 双参量响应面拟合多项式系数
从图9、10中箭头所指位置可见,设计的均衡优化模型所得到的最优解在满足应力降低目标的同时,选择了指数相对较小,即异型度较小的均衡解(因超椭圆指数与异型度成单调递增关系,图2)。此时,最优解附近响应面变化较为平缓,设计具有较好的稳健性[20-21]。
4.2 设计灵敏度分析
在结构的优化中,灵敏度分析作为反映稳健性的重要指标日益得到重视[22-23]。对于结构复杂的优化问题,其功能函数不能明确表达时,灵敏度分析常采用响应面法获得[24]。考虑到超椭圆孔孔边应力降低率随指数变化基本连续,且数学模型简洁,变量较少,采用对响应面的拟合多项式求导数和偏导数的方式来计算其最优解附近的灵敏度。对式(11)和(12)分别求导,绘制其灵敏度随指数变化的曲线,如图11、12所示。
图中箭头所指为最优解,在2种情况下,其所在区域的指数灵敏度都相对较小。这意味着优化得到的超椭圆螺栓孔不会因为轮廓的微小变化而产生过于明显的孔边应力变化,并表明均衡优化所获得的超椭圆螺栓孔设计点具备较好的稳健性。这在一定程度上也对未来加工误差的控制和加工方法的选择提供了方便。

图11 单参量超椭圆孔指数灵敏度

图12 双参量超椭圆孔指数灵敏度
5 结论
本文针对轮盘螺栓孔孔边应力集中问题提出了1种超椭圆螺栓孔均衡优化方法,得到以下主要结论。
(1)提出的超椭圆螺栓孔设计方法均衡考虑了2个相互制约的目标函数,得到的超椭圆螺栓孔能按设计需求有效降低孔边应力,且孔轮廓异型度较小,保证了可靠的传力。
(2)超椭圆孔数学模型简洁,设计变量更少,寻优空间更易把握,优化效率和稳定性较高。
(3)均衡优化获得的超椭圆异型孔应力响应灵敏度较小,设计稳健性较好。
[1]杨俊,李承彬,谢寿生.涡轮盘多轴低循环疲劳寿命预测及试验验证[J].航空动力学报,2011,26(10):2220-2226.YANGJun,LIChengbin,XIE Shousheng.Multiaxial low cycle fatigue life prediction and test verification for turbine disk[J].Journal of Aerospace Power,2011,26(10):2220-2226.(in Chinese)
[2]陆山,黄其青.涡轮盘销钉孔损伤容限分析新方法及其应用 [J].航空动力学报,2002,17(1):87-92.LU Shan,HUANG Qiqing.New method for damage tolerance analysis of turbine disk and its application[J].Journal of Aerospace Power,2002,17(1):87-92.(in Chinese)
[3]袁红璇.现代高寿命飞机的连接技术 [J].航空工程与维修,2002(3):46-47.YUAN Hongxuan.Connecting techniques of the modern long life aircraft[J].Engineering&Technology,2002(3):46-47.(in Chinese)
[4]Shi Y,Wang M,Wang Y.Analysis on shear behavior of high-strength bolts connection[J].International Journal of Steel Structures,2011,11(2):203-213.
[5]张超.涡轮连接单元异型孔应力场分析及结构优化[D].南京:南京航空航天大学,2014.ZHANG Chao.Stress field analysis and structural optimization of non-circular hole on flange of turbine disks[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2014.(in Chinese)
[6]刘庆瑞,刘玉萍.发动机第4级压气机盘裂纹失效分析 [J].航空发动机,1999(2):38-41.LIU Qingrui,LIU Yuping.Failure analysis of the fourth stage of compressor disc on areoengine[J].Aeroengine,1999(2):38-41.(in Chinese)
[7]陈秋任,郭海丁,刘小刚.涡轮盘双轴对称异形孔结构建模与优化[J].航空动力学报,2013,28(6):1250-1256.CHEN Qiuren,GUO Haiding,LIU Xiaogang.Modeling and optimization for the structure of biaxial symmetry non-circular hole of turbine disk[J].Journal of Aerospace Power,2013,28(6):1250-1256.(in Chinese)
[8]郭海丁.一种圆弧和直线段混合异型孔:中国,201510430090.2[P].2015-11-11.GUO Haiding.A mixing non-circular hole of circular arc and straight line segment:China,201510430090.2[P].2015-11-11.(in Chinese)
[9]Allaire G,Jouve F,Toader A M.Structural optimization using sensitivity analysis and a level-set method[J].Journal of Computational Physics,2004,194(1):363-393.
[10]Schleich B,Wartzack S.A generic approach to sensitivity analysis in geometric variations management[C]//Proceedings of the 20th International Conference on Engineering Design.Italy:the Design Society,2015:343-352.
[11]Hankerson D,Vanstone S,Menezes A.Guide to elliptic curve cryptography[M].New York:Springer New York,2004:70-80.
[12]Ulas M.Rational points on certain hyper-elliptic curves over finite fields[J].Bulletin of the Polish Academy of Sciences Mathematics,2007,55(2):97-104.
[13]DAI Longchao,GUO Wanlin,WANG Xinwei.Stress concentration at an elliptic hole in transversely isotropic piezoelectric solid[J].International Journal of Solids&Structures,2006,43(6):1818-1831.
[14]彭铁红,侯兆欣,文双玲,等.螺栓孔径与孔型对高强度螺栓摩擦型连接承载能力影响的试验[J].钢结构,2007,22(7):30-34.PENG Tiehong,HOU Zhaoxin,WEN Shuangling,et al.Experiment of effects of hole diameter and hole type on bearing capacity of high strength bolt frictional joints[J].Steel Construction,2007,22(7):30-34.(in Chinese)
[15]国家钢结构工程技术中心.JGJ82-2011钢结构高强度螺栓连接技术规程[M].北京:中国建筑工业出版社,2011:8-14.National steel structure engineering technology center.JGJ82-2011,Technical specification for high strength bolt connections of steel structures[M].Beijing:China Building Industry Press,2011:8-14.(in Chinese)
[16]胡鹏天.扩孔对高强度螺栓连接抗剪承载性能的影响分析 [D].北京:清华大学,2014.HU Pengtian.Investigation on bolted connection with enlarged holes under static shear[D].Beijing:Tsinghua University,2014.(in Chinese)
[17]陈光.航空发动机结构设计分析[M].2版.北京:北京航空航天大学出版社,2006:176.CHEN Guang.Aviation engine structure design and analysis[M].2nd ed.Beijing:Beihang University Press;2006:176.(in Chinese)
[18]Ruiz A B,Luque M,Ruiz F,et al.A combined interactive procedure using preference-based evolutionary multi-objective optimization[J].Expert Systems with Applications,2015,42(21):7466-7482.
[19]Coello CA.Evolutionary multi-objective optimization:A historical view of the field[J].IEEE Computational Intelligence Magazine,2006,1(1):28-36.
[20]Deb K,Pratap A,Agarwal S,et al.A fast and elitist multi-objective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[21]CHEN Qiuren,GUO Haiding,ZHANG Chao,et al.Structural optimization of uniaxial symmetry non-circular bolt clearance hole on turbine disk [J].Chinese Journal of Aeronautics, 2014(5):1142-1148.
[22]贡金鑫,赵国藩.国外结构可靠性理论的应用与发展[J].土木工程学报,2005,38(2):1-7.GONG Jinxin,ZHAO Guofan.Application and developments of structural reliability theory abroad[J].China Civil Engineering Journal,2005,38(2):1-7.(in Chinese)
[23]蔡斌,邢海丰.响应面法在可靠性灵敏度分析中的应用[J].机械设计与研究,2016,32(4):28-30.CAI Bin,XING Haifeng.Reliability sensitivity analysis based on response surface method[J].Machine Design and Research,2016,32(4):28-30.(in Chinese)
[24]李昌,韩兴.基于响应面法齿轮啮合传动可靠性灵敏度分析[J].航空动力学报,2011,26(3):711-715.LI Chang,HAN Xing.Analysis of reliability sensitivity for gear engagement based on response surface methods[J].Journal of Aerospace Power,2011,26(3):711-715.(in Chinese)

