基于大涡模拟的圆转矩喷管尾喷流强化掺混机理研究

李经警，张 勃，张纳如，吉洪湖，叶留增，许 羚

（1.南京航空航天大学能源与动力学院，南京210016；2.中国航发沈阳发动机研究所，沈阳110015）

0 引言

湍流是流体力学研究中的1个世界性难题，而圆湍射流作为组成旋转射流、冲击射流及燃烧室流动等复杂流动的基本流动形式，已广泛应用于农业灌溉、燃油雾化、发动机气膜冷却等多种领域。

就航空发动机而言，其尾喷流是飞机尾向3～5 um波段上的主要红外辐射源之一，强化尾喷流掺混，减小其核心区温度是降低相应波段红外辐射特性的有效手段[1]。而圆转矩2元喷管因其红外抑制等方面的优良效果，在多款先进战机如F-117、F-22上得到应用，数值模拟与试验结果也发现，采用2元喷管后其掺混效果[2]和红外抑制特性相比轴对称喷管显著增强[3]。因而从机理上弄清圆转矩喷管与轴对称喷管尾喷流的发展过程，及掺混过程的影响因素就极为必要。不仅可以为异形喷管的强化掺混机理提供依据，也能为喷管修型提供设计思路。国内外针对异形喷管尾喷流强化掺混的机理研究已有一定进展，但对于其作用机制仍不够明朗[4-5]。在试验方面，利用PIV等测量手段可以得到射流中湍流运动的流动特性和卷吸过程大尺度涡结构的变化情况[6-7]。但由于湍流运动中涡旋数量巨大且发展迅猛，受到测量设备的限制，试验往往不能获得研究者所关心的全部细节；通过数值模拟可以对卷吸过程中拟序结构的产生、发展进行细致研究，如尾迹涡、剪切涡、发卡涡、肾形涡对等[8-9]，能够更好地从机理上了解卷吸过程，揭示喷管形式对涡结构演变的影响机理。而数值模拟与试验对比研究结果表明：与其他计算模型相比，在近场区应用大涡模拟可以得到更准确的结果[10-11]，且计算成本适中。

本文主要采用数值计算的方法，对轴对称喷管以及圆转矩形喷管的流动特性进行模拟。研究采用可压缩流大涡模拟（LES）控制方程动态亚格子模型进行，对喷管尾喷流核心区长度与卷吸掺混面积变化，涡量和雷诺剪切应力分布，以及射流场拟序结构发展变化等方面进行比较分析。

1 物理模型与算法

1.1 物理模型

研究模型为：轴对称收敛喷管（Model-A）和圆转矩形收敛喷管（Model-B），尺寸分别如图1、2所示。喷管进口直径Dn均为10 mm，长度均为15 mm。

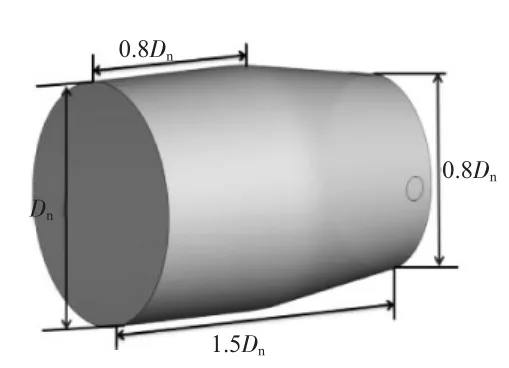
图1 轴对称喷管Model-A物理模型

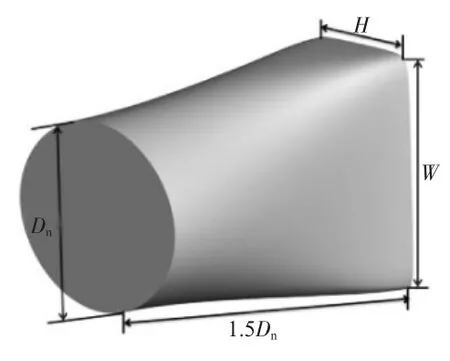
图2 圆转矩喷管Model-B物理模型

Model-A：出口直径D=8 mm，平直段长度为8 mm，收敛段长度为0.7 mm；

Model-B：当量直径定义为：D=4 A/C，同样为8 mm，宽高比 W/H=2。

1.2 模拟算法

数值模拟采用LES方程的动态Smagorinsky模型，非稳态条件。

首先通过滤波将瞬时变量φ（x,t）划分为大尺度量x,t）和小尺度量φ'（x,t）x,t）通过以下加权积分得到

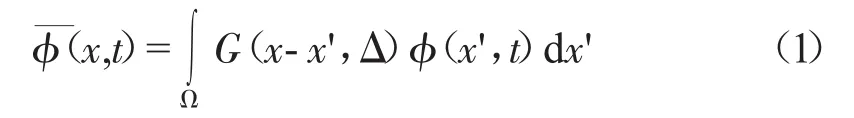
式中：G（x-x',Δ）为滤波函数；Ω 为计算区域；Δ 为滤波的宽度，与网格分辨率有关。

而将式（1）表示的滤波函数处理瞬时状态下不可压缩流N-S方程时，有

连续性方程

动量方程

能量方程

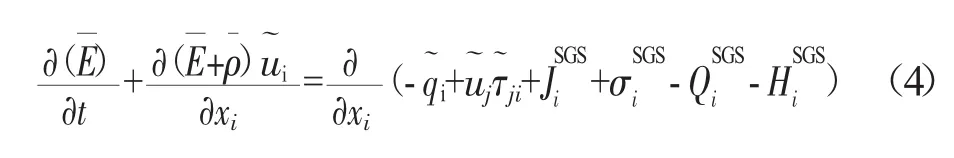
式中：上标“－”表示空间过滤，“～”表示Favre过滤，上标“SGS”代表亚格子（未封闭项）；ρ、ui和p分别为密度、速度和压力；τij为黏性通量项；DijSGS为亚格子黏性应力项；E为总能；qi为热通量项；JiSGS为亚格子湍流扩散项；QiSGS为亚格子黏性扩散项；QiSGS亚格子热通量项；HiSGS为亚格子能量通量项；τijSGS为亚格子应力项，模型的思想沿袭了RANS中的涡黏性模型，其表达式为

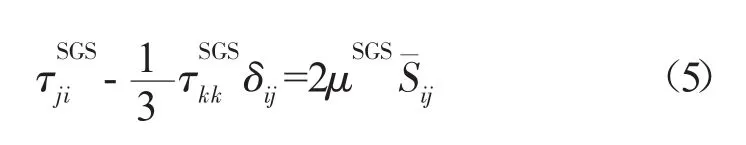
式中：μSGS为涡黏系数，可以从亚格子模型中求出。

在该模型中

因此

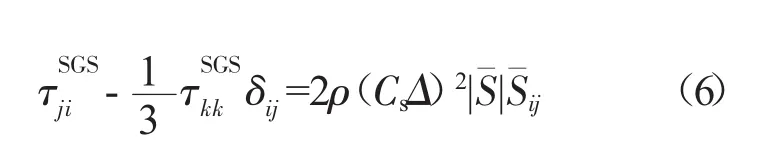
式中；Cs为Smagorinsky常数，取决于流体中的运动状态和性质。

式（6）即为考虑小涡影响后得到的应力项（亚格子应力）。

1.3 计算域与边界条件

以Model-B为例对其计算域（如图3所示）进行说明。其直径为160 mm，长度为300 mm；喷管出口在y-z平面，流动方向为x轴正向，宽边侧为y向，窄边侧为z向。

图3 喷管计算域

具体边界条件为：喷管进、出口为压力进、出口条件，压比NPR=1.52，进口总温T*=600 K；出口温度为310 K；喷管壁面为绝热条件，同时不考虑辐射传热；最终喷管模型出口流速为 Ma=0.8，高雷诺数（Re=2×105）。

时间步长

式中：Δxmin为流向网格最小分辨率；Ujmax为喷管出口最大流速；本文取Δt=2.5e-6s，计算总时间t=0.02 s，流场分析取最终时刻t=0.02 s的流场进行。

1.4 网格划分

为更好捕捉射流与尾喷流相互作用区域的流动细节，在喷管壁面附近和射流中心区进行网格加密（间距沿x,z正方向逐渐变大），圆转矩模型网格分布如图4所示。

经网格无关性检验和考虑模拟精确程度，最终Model-A、B所取节点数均在530万左右。

2 计算结果分析

2.1 模型温度分布

模型轴向截面温度分布如图5所示。图中黑色实线表示核心区长度 L（Model-A，L=69.2 mm；Model-B，L=48.5 mm,和文献 [12-13]试验结果符合较好）；以Model-A为基准L0，核心区长度变化率C=|（L0-L）/L0|，从图中可见，Model-B射流核心区长度缩短了29.9%；Model-A射流的温度分布形状与Model-B窄边侧相似,呈尖锥形,温度峰值出现在中心线上；而Model-B宽边侧的温度分布则呈现多峰状态,在中心线的两侧出现多个波动的峰值,这是由于环境流体卷入后核心区流体扰动增强导致的，使得与环境冷气流掺混区域增大。

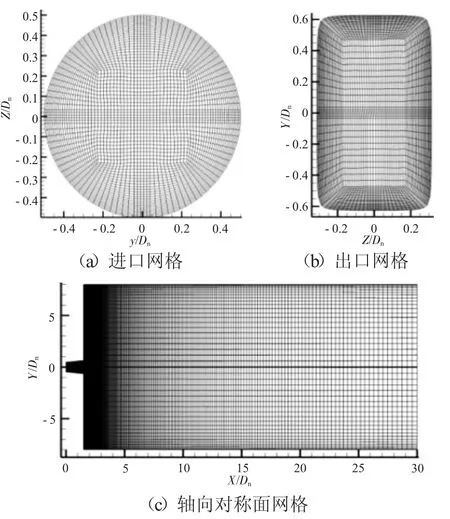
图4 计算模型B网格

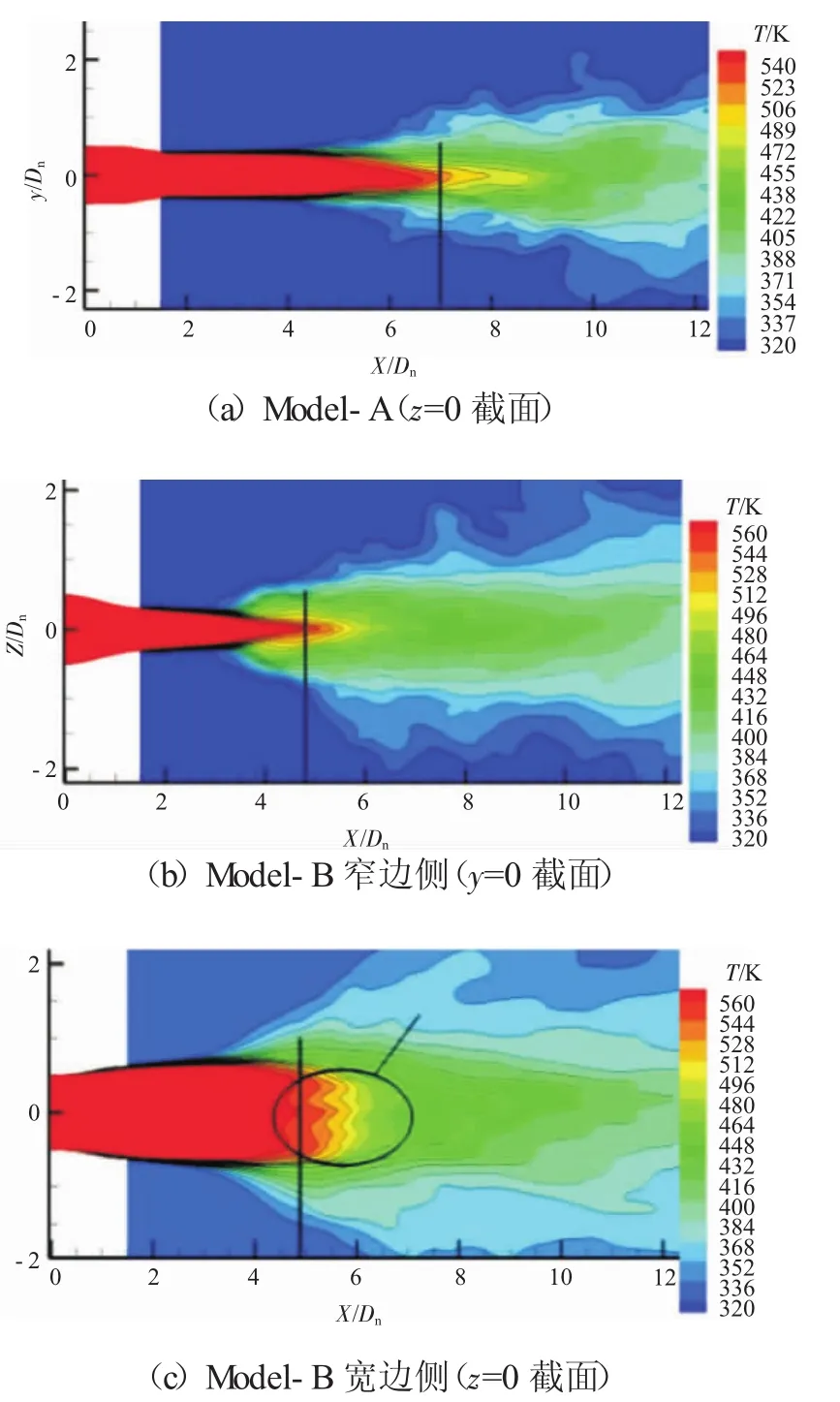
图5 轴向平均温度分布

2.2 模型速度分布

模型射流中心线上无量纲速度（U/Uj）分布如图6所示。从图中可见，在喷管内部，2个模型速度逐渐增加；在喷管出口初始段存在1段速度不变的区域（核心区）；但随着射流与环境之间能量、动量交换增强，射流动能降低，速度逐渐减小。圆转矩模型Model-B核心区长度缩短，速度衰减加快；在完全发展段（X/Dn＞10），轴对称模型Model-A与圆转矩模型Model-B射流速度分布已基本一致。

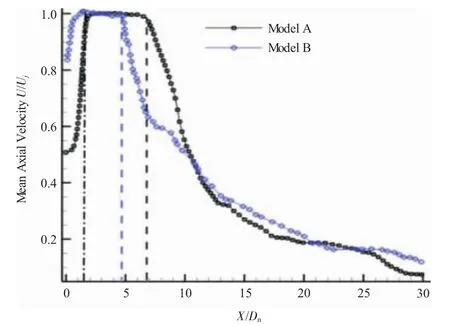
图6 射流中心线上无量纲平均速度分布

模型在不同截面上速度沿径向变化如图7所示。在图7（a）中将Model-A与Model-B对应截面上的窄边数据进行比较，在X/Dn=2截面上,核心区的速度基本不变，受环境气流影响较小，而射流扩散受到出口截面的影响，Model-B窄边侧核心区宽度相比模型A较小；在X/Dn=5截面上，射流脱离了核心区，速度峰值出现在中心轴线处，沿径向逐渐减小，Model-B速度略低于Model-A的，这是由于其掺混较强导致的；在下游较远处的X/Dn=10截面上，喷管出口形状的影响逐渐减弱，Model-A与Model-B的速度分布基本相同，二者达到自模状态。

在图7（b）中比较了Model-B宽边侧与Model-A的速度。从图中可见，Model-B心区宽度（X/Dn=2截面）大于Model-A的，且在X/Dn=5上，其速度出现双峰现象，这与图5（c）的温度脉动特征吻合。进一步表明CVP结构的内旋,导致速度脉动加强，但随着射流不断向前卷吸发展，速度脉动减弱，Model-B双峰现象逐渐消失，在下游远场（X/Dn=10），Model-A与Model-B的2种模型的径向速度分布也逐渐一致。

图7 径向截面中心线无量纲平均速度

2.3 模型掺混特性

采用大涡模型对射流掺混进行模拟，能够描绘出其射流拟序结构随时间和空间的变化，有利于深入理解射流掺混过程。

在涡核分析过程中采用目前应用较广Q准则来识别旋涡结构[14]

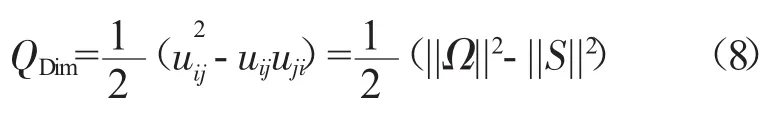
式中：Ω为涡量幅值，表示旋转；S为应变率幅值，表示变形；Q为转动速率超过应变率的程度。

根据Q准则显示出的尾喷流瞬时拟序结构如图8所示，颜色由速度场着色得到。从图中可见，在流场中涡旋结构主要由涡环、涡辫、发卡涡、螺旋涡组成。Model-A、B射流场涡核发展过程大致相同。等比放大模型（其保证Re相同）的尾喷流瞬时红外热成像如图9所示。将图8在不同时刻射流与环境卷吸过程中拟序结构的变化，与图9中尾喷流的红外热像图进行对比，保证了模拟的可靠性。

图8 不同时刻涡结构Q等值面（采用速度场着色）

以Model-A为例，从图中可见，当射流从喷管出口流出，与环境气流掺混作用较弱，由于射流剪切层比较稳定，诱导出的涡结构较小，存在1段光滑区。在射流向前发展的过程中，气流向内螺旋汇聚，破坏速度剪切层，形成涡环结构；其在剪切作用下会逐渐拉伸，而后脱落（脱落频率受剪切层脉动影响），随后向内卷吸的气流在射流剪切作用下，又形成新的涡环。

同时可见，受到涡环外侧反向速度的拉伸，使连接2个涡环之间的涡管结构生长，这部分结构称为涡辫。该结构是在流动向下游发展的过程中,由于涡环之间的非线性不稳定作用增强，射流脉动较强的条件下逐渐形成的。

随着流动进一步发展，射流柱在剪切作用下脉动特征加强，涡环之间的距离缩小，涡环与涡辫之间相互作用增强，最终形成尺度较大的发卡涡，使射流柱表面呈鱼鳞状；随着射流继续向下游发展，射流脉动减弱，大尺度发卡涡被耗散成更多小尺度的螺旋涡结构。

图8中Model-A、B均具有典型的涡环、涡辫、发卡涡、螺旋涡结构，以及射流柱初始的光滑段和过渡段的鱼鳞状表面[15-16]。

而比较图8在t=0.02 s时刻的拟序结构与图9的试验结果可知：当Re相同时，在类比试验中也可见射流近场掺混较弱，射流柱较光滑，以及边界层在卷吸过程中形成的剪切涡；同时在向下游发展的过程中较大尺度的涡旋逐渐耗散，射流柱逐渐失稳，涡旋结构增多，呈现出鱼鳞段表面；而圆转矩模型核心区长度较轴对称模型短，近场涡旋耗散得更多，射流柱脉动得更剧烈。

进一步比较各时刻的拟序结构可知2种喷管射流与环境气流卷吸掺混特征之间的区别。

比较图8中的t=0.0006 s时刻，轴对称模型Model-A和圆转矩模型Model-B拟序结构可见：在初始时刻，轴对称射流向外卷吸范围比较小，涡结构较少，但圆转矩模型在出口边角存在涡管，诱导出的涡环也离喷管出口的距离更近（图中I线），同时发卡涡形成得也更早（图中II线）；这是由于圆转矩模型射流受喷管出口截面的影响，边界层减薄，出口拐角处诱导出较强的二次涡流。

在图8中Model-A在t=0.0022 s时刻的涡核结构可见在涡环形成—脱落—形成的过程中，涡辫会断裂，且随着射流发展涡环之间的距离逐渐减小；同时Model-B在同样时刻可以观察到：在圆转矩模型核心区宽边侧诱导出的涡尺度更大，涡辫区螺旋涡交搭形成发卡涡更早。

比较图8在t=0.005 s时刻的拟序结构，可见在射流的初始段和过渡段分别呈现出比较明显的光滑段表面和鱼鳞状表面；圆转矩模型在射流核心区内发卡涡的尺度更大，说明Model-B射流柱表面波尺度更大，速度剪切层脉动得更剧烈；Model-B发卡涡密集区也离出口更近，相互之间汇聚、交搭的频率更高，诱导出的发卡涡更多；以上几个时刻的比较说明Model-B近场涡结构更丰富。

而同样比较图8在t=0.02 s的拟序结构，可见在完全发展段2种模型的涡核发展情况基本一致，均以螺旋涡结构为主。

图9 喷管尾喷流瞬时红外热成像

雷诺应力能表征湍流脉动强弱，因此通过比较2个模型雷诺剪切应力特征，可以反映其射流剪切层内流体脉动状况，进一步反映二者在掺混特性的区别。

宽边侧无量纲雷诺剪切应力

窄边侧无量纲雷诺剪切应力

式中：u为x向脉动速度；v，w分别为y、z向脉动速度；U0为喷管出口截面平均速度。

模型Model-A和Model-B在不同截面沿径向中心线雷诺剪应力分布分别如图10～12所示。

图10 Model-A径向截面中心线雷诺剪切应力分布

图11 Model-B宽边侧径向中心线雷诺剪应力分布

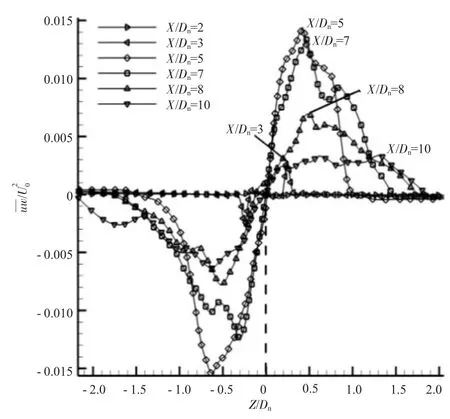
图12 Model-B窄边侧径向中心线雷诺剪应力分布

图10～12中Model-A、B的径向雷诺应力分布表明：在不同截面雷诺剪应力从中心轴线沿径向均先增大后减小。以图10中X/Dn＝7处的曲线为例，其中心线（y/Dn=0）上的雷诺剪应力最小，随着径向距离增大而逐渐增大，在剪切层边界附近达到最大，在这个区域附近射流与外界气流发生剧烈掺混，能量耗散加剧，而后沿径向剪切应力逐渐减小[17-18]。其中轴对称模型应力分布与圆转矩模型的窄边侧相似，但受出口截面影响，圆转矩射流在宽边侧边界层更薄，脉动更剧烈，从图11中可见，在核心区边缘附近（X/Dn=5、7）应力分布出现多峰脉动现象。

同样在不同径向截面应力沿轴向分布的结果可见：在射流扩张过程中，应力峰值沿轴向先增大，然后再逐渐减小，最大值出现在核心区边缘（Model-A大致在X/Dn=7、Model-B在X/Dn=5）。在离喷管出口较近的初始段，刚开始雷诺剪应力较小，符合前文提到在初始段拟序结构较少，射流柱表面呈光滑段的特征；在过渡段雷诺剪切应力较大，射流柱脉动较强，也佐证了射流柱在过渡段表面波尺度加大，呈鱼鳞状的特征；而在完全发展段X/Dn=10，雷诺剪切应力均较小，说明随着大尺度涡被耗散，射流脉动较小，也验证了此区域以较小尺度的螺旋涡结构为主的特征。

而比较图10～12的结果可见，在初始段同样轴向位置圆转矩模型Model-B的雷诺剪切应力峰值较大，例如Model-B在X/Dn=3的数值已较大，在X/Dn=5已达至最大，且峰值更高、脉动次数更多，说明圆转矩模型射流脉动更剧烈，也佐证了上述圆转矩模型诱导出的涡环、发卡涡结构离喷管出口更近、出现时刻更早，即射流柱失稳更近更早的观点。

比较图11、12的结果可见，在圆转矩喷管射流中，宽边侧剪切应力较大，下降幅度较快，说明其宽边侧速度脉动较强，这是由于宽边侧诱导出的发卡涡更多，拟序结构更复杂导致的。

3 结论

采用LES动态亚格子模型，对轴对称和圆转矩2种喷管在亚声速（Ma=0.8）、高雷诺数（Re=2×105）条件下射流与外流的强化掺混特性进行了数值模拟，分析比较了不同喷管流场流动特性，拟序结构变化、涡量和雷诺剪应力分布等规律，对矩形喷管强化掺混机理进行初步探讨，主要结论如下：

（1）与轴对称模型相比，圆转矩模型射流核心区长度减小29.9%，中心线上速度衰减更快，核心区与外界冷流掺混范围更大，核心区高温面积更小。

（2）轴对称喷管射流与圆转矩形喷管射流拟序结构发展过程相似：均包括射流初始段的光滑段表面，以剪切涡环和涡辫结构为主；过渡段的鱼鳞段表面，以发卡涡结构为主；以及完全发展段，以螺旋涡为主；但圆转矩射流在近场诱导出的剪切涡环、发卡涡结构发展更快，边角剪切涡环也形成了典型的CVP结构，导致其涡旋耗散率增加，大尺度的发卡涡更易耗散成螺旋涡，近场涡旋更丰富。

（3）轴对称喷管与矩形喷管射流雷诺剪切应力沿径向均先增大后减小,在射流与外流交界面上达到最大；沿轴向，应力峰值同样先增大再减小，在核心区边缘达到最大；且二者在射流远场应力分布趋于相似。但与轴对称模型相比，圆转矩模型应力峰值在轴向位置离喷管出口更近；在窄边侧二者应力分布相似，但圆转矩模型在轴向相同位置的应力峰值增大；且同样相比窄边侧，其宽边侧应力峰值进一步增大，衰减速度也更快，在核心区边缘附近还出现应力多峰脉动现象；以上均说明圆转矩喷管在射流近场速度剪切层内的脉动更强，与外界气流进行动量交换的效率更高。

（4）拟序结构发展及剪切层内雷诺剪切应力变化均说明在射流流场中涡旋发展耗散速度快、速度边界层脉动强、射流柱易失稳是导致射流核心区长度减小，掺混增强的本质因素，这也是强化掺混异形喷管设计过程中的研究方向所在。

[1]蒋耀庭,王跃.红外隐身技术与发展[J].红外技术，2003,25（5）:7-9.JIANG Yaoting,WANG Yue.Technology and development of infrared stealthy[J].Infrared Technology，2003，25（5）:7-9.（in Chinese）

[2]张勃，吉洪湖，黄伟，等.圆转矩形喷管射流掺混特性试验[J].航空动力学报，2009，24（11）:2476-2482.ZHANGBO，JIHonghu，HUANGWei，et al.Experimental investigation of mixing characteristics of jet from circle-rectangular transition nozzle[J].Journal of Aerospace Power，2009，24（11）:2476-2482.（in Chinese）

[3]张勃，吉洪湖,罗明东，等.宽高比对尾向可见明火矩形喷管红外抑制特性影响研究[J].航空动力学报，2007，22（11）:1820-1825.ZHANG Bo,JI Honghu,LUO Mingdong，et al.Research of the influence of aspect ratio on infrared suppressing characterstics of rectangular nozzles[J].Journal of Aerospace Power，2007，22（11）:1820-1825.（in Chinese）

[4]Underwood D S,Waitz I A.Effect of heat release on streamwise vorticity enhanced mixing [J].Journal of Propulsion and Power，1995，12（4）:638-645.

[5]单勇，张靖周.波瓣喷管引射-混合器的数值研究与验证[J].推进技术,2004,25（4）:320-324.SHAN Yong，ZHANG Jingzhou.Numerical computation and examination of a lobed mixed-ejector[J].Journal of Aerospace Power，2004，25（4）:320-324.（in Chinese）

[6]Fric T F,Roshko A.Vortical structure in the wake of a transverse jet[J].Journal of Fluid Mechanics，1994，279:1-47.

[7]李炜，姜国强，张晓元.横流中圆孔湍射流的旋涡结构[J].水科学进展，2003，14（5）:578-582.LI Wei，JIANG Guoqiang，ZHANG Xiaoyuan.Vortex structures of round turbulent jets in cross-flow[J].Advances in Water Science，2003，14（5）:578-582.（in Chinese）

[8]张燕.射流冲击射流涡旋结构的实验和数值研究[D].上海:上海大学，2005.ZHANGYan.Experimental and numerical investigations on the vertical structures of an impinging jet in cross flow[D].Shanghai:Shanghai University，2005.（in Chinese）

[9]史万里.涡轮流场大涡模拟与拟序结构研究 [D].南京:南京航空航天大学,2012.SHI Wanli.Investigation of large eddy simulation and coherent structure for the flow field of turbine vane[D].Nanjing:Nanjing University of Aeronautics and Astronautics，2012.（in Chinese）

[10]Chauvet N,Deck S,Jacquin L.Numerical study of mixing enhancement in a supersonic round jet[J].AIAA Journal，2007，45:1675-1687.

[11]Galeazzo F C C,Georg D.Measurement and simulation of turbulent mixing in a jet in cross flow[J].ASME Turbo Expo:Power for Land,Sea,and Air,2010,133（6）:571-582.

[12]张勃,吉洪湖.大宽高比矩形喷管的射流与外流掺混特性的数值研究[J].航空动力学报,2005,20（1）:104-110.ZHANG Bo，JI Honghu.Numerical study of internal and external flow mixing for rectangular nozzles with large aspect ratio[J].Journal of Aerospace Power，2005，20（1）:104-110.（in Chinese）

[13]Kamran M A，Mcguirk JJ.Unsteady predictions of mixing enhancement with steady and pulsed control jets[J].AIAA Journal,2015,53（5）:1262-1276.

[14]Jeong J，Hussain F.On the identification of a vortex [J].Journal of Fluid Mechanics，1995，285:69-94.

[15]Hinze J O．Turbulence[M].New York:McGraw-Hill Publishing Co.,1975:133-488.

[16]范全林，王希麟，张会强，等.圆湍射流拟序结构研究进展[J].力学进展,2002，32（1）:109-118.FAN Quanlin，WANG Xilin，ZHANG Huiqiang,et al.Coherent structures in turbulent round jet[J].Advances in Mechanics，2002，32（1）:109-118.(in Chinese)

[17]Krothapali A,Aganoff D.On the mixing of a rectangular jets[J].Journal of Fluid Mechanics,1981,107:201-220.

[18]Suchiya Y,Horikoshi C.On the spresding of rectangular jets[J].Experiments in Fluid，1986(16):197-204.