基于模块化设计的车身装配结构优化∗

单春来，李永成，侯文彬

(1.大连理工大学，工业装备结构分析国家重点实验室，大连 116024； 2.大连理工大学汽车工程学院，大连 116024)

前言

随着工程技术的不断发展和国民消费水平的不断提高，汽车销量也在持续攀升，汽车厂商间的竞争也随之愈演愈烈，新车型的上市速度越来越快。为保持市场竞争力，世界各大汽车厂商通过使用模块化设计的研发和生产制造方式代替传统方式，大大缩短了汽车开发周期[1]。近年来，国内的汽车企业也认识到了模块化设计的重要性并开始采用模块化生产制造方式，逐步向国际先进汽车厂商靠拢[2]。

汽车模块化战略的优势在于零部件的高度通用性。通过零部件在不同车型之间共用来减少模具成本，缩短新车型的开发周期[3]。因此，采用模块化设计方式制造的车身必然不同于传统制造方式。另外，概念设计阶段决定了70%的总体成本和主要的车身性能[4]，因此，在概念设计阶段就应进行车身制造装配方式的研究。对车身而言，主要的结构性能指标为车身刚度(影响驾驶感受、NVH性能和安全性能等[5])、可装配性(影响制造难度、装配成本和结构可靠性等[6])和可制造性(评估制造风险及成本[7])3个方面。本文中将从这3个方面出发，研究概念阶段的车身模块化制造装配结构。

本文中对图分解法进行改进，以车身刚度、装配成本和制造成本为优化目标，提出一种基于车身制造装配的零部件分割方式[8]；对算法中加入板厚变量时计算无法收敛的问题提出二次择优算法；针对解集选优提出一种基于模糊集合理论的评分公式，实现整套车身制造装配设计流程；最后以某车身底板为算例，验证方法的实用性。

1 改进的图分解法

1.1 图分解法

装配结构优化研究如何将结构进行分解以及该分解方案带来的结构性能和装配与制造成本的变化。该问题是对3个性能指标进行评判的离散问题，须选用能处理离散问题的多目标优化算法[9]。图分解算法主要用于结构分解并能与进化算法高效结合，最适用求解这类问题[10]。

“图”用以描述事物及其之间的联系[11]，借助将工程结构转化成“图”的方式可对任意包含二元关系的离散系统创建相应的数学模型。式(1)为图分解算法的基本数学模型，x为分割向量。可以看出，图分解法十分易于二进制编码。

图1为图分解法的示意图。图1(a)中截面可分割为图1(b)中5个基本单元，对应拓扑图如图1(c)所示。图1(c)中节点代表图1(b)中的基本单元，边代表单元间的连接。图1(e)中拓扑图移除边E2，E3，E5和 E6，其连接关系就对应于图 1(d)结构图。

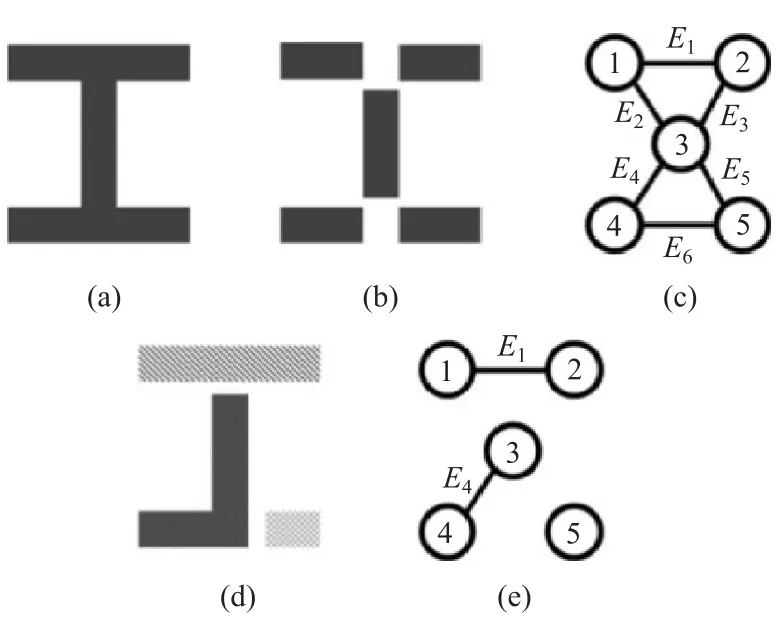
图1 拓扑图分割过程示意图

1.2 改进的图分解法

分割后的拓扑图对应实际结构的制造方式，因而结果必须具有合理性。图2为某不合理的结果。矩形结构图2(a)分解为图2(b)中4个基本单元，拓扑图如图2(c)，图2(d)为移除边E2后形成的子图，图2(e)为图2(d)映射的结构图。由图2(e)不难看出，这种制造方式是不合理的，制造底板时，在整块钢板中不会单独存在一条焊缝。

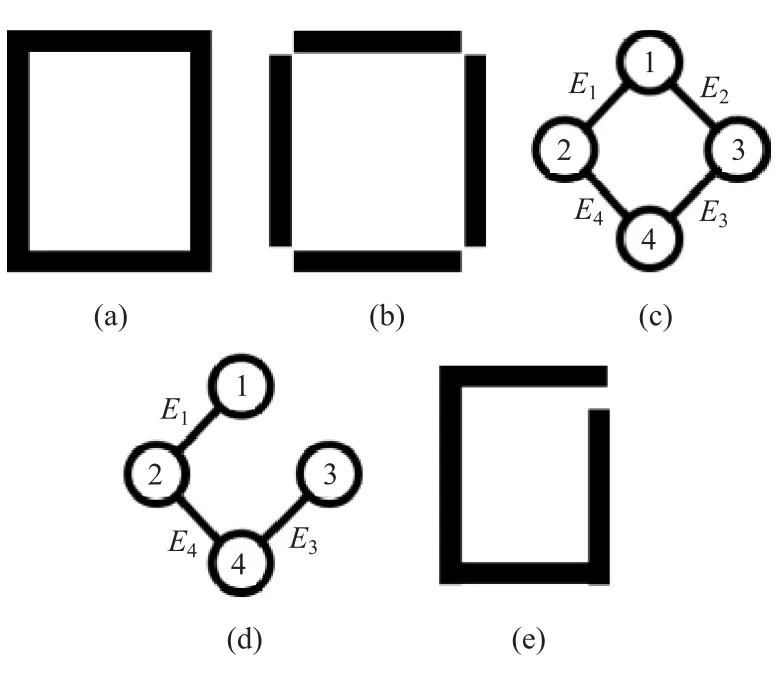
图2 被不合理分割的结构图产生过程

为解决这样的问题，可根据预定规则对不合理的结果进行修正，规则可为:被完整分割下来的子图中包含的连接关系应和父图中的一致[12]。即保证了父图合理，分割下来的子图就合理。其修正公式为

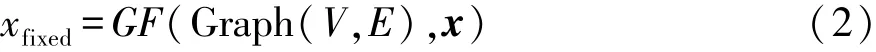
式中:Graph(V，E)为父图的信息；x代表分割向量；函数GF为修正函数。GF(·)根据输入的父图信息和分割向量对x进行修改，保持整体分割方式不变，将子结构内部的连接关系修正为跟初代个体一致，并返回修正后的分割向量xfixed用于计算目标函数。本文在MATLAB中通过调用view(biograph(A))函数(得到子图分块信息)和graphconncomp(A)函数(得到部件分割数量和节点归属数组)，对拓扑图中连接关系的稀疏矩阵进行子部件连接关系的替换，实现对子图的修正。用深度优先搜索算法可较好地得到xfixed[13]。该方法可避免不合理个体的产生，优化过程中因产生不合理个体而导致优化方向出现偏差的问题得到了抑制，种群中个体数量的减小也提高了优化速度，节省了计算时间。

2 二次择优方法

2.1 问题分析

对车身底板进行装配方式设计时，板厚的变化会影响装配方式的设计，应考虑各部件厚度的影响。图3所示为某车身底板。按照可制造尺寸将设计区域分割为12块制造单元(车身结构具有对称性，只需取一半作为研究对象)，图中点划线对应为潜在焊接位置(共17处)。使用前面提出的方法，将焊接位置作为设计变量进行编码，如x2代表位置2处的焊接情况:值为1时处于子部件内部，不存在焊缝；值为0时为两个子部件的交界，存在焊缝。以结构刚度、制造成本和装配成本为目标函数进行优化，将图3中各制造单元分别赋予相同板厚和不同板厚进行求解，分别求得最优解集，如表1所示。

图3 某车身底板装配结构优化设计

由计算结果可以看出，不同的板厚会得到不同的装配方式，因此在进行装配方式的优化时须考虑板厚的影响，否则在后期对板厚进行单独优化时难以保证得到的是最优设计。但由于存在以下两个问题，不能将板厚作为设计变量直接加入到优化模型中:

(1)将板厚变量直接加入到优化模型中，会由于板厚变量和分割向量对目标函数灵敏度不在同一数量级等原因，导致模型无法收敛；

表1 车身底板装配方式解集

(2)在概念设计阶段，分割后的子部件应作为等厚度板进行设计，即分割后的子图中需要约束各制造单元的厚度保持一致。

图4为某底板根据制造单元进行预分割的示意图，图中t代表制造单元的板厚。如果划分结果中两块单元同属一个部件，则应有tn＝tn＋1；如果分属两个部件，则无此约束。

图4 单元板厚度关系

为解决问题(1)，应将优化模型设计为多层次优化结构，将分割向量和板厚变量分别作为两个层次的自变量，分别优化并进行迭代；为解决问题(2)，则应在对每一次分割向量求解完毕后，迭代给板厚变量优化前加入约束函数，从而保证厚度变量的正确约束。本文中为解决这两个问题，提出了一种多层次二次择优的算法结构。

2.2 算法结构

根据对问题的分析，本文中提出的算法结构如图5所示。对使用图分解算法得到的分割结果进行二次择优:首先不考虑子部件内部板厚要求一致的约束，直接对图分解法得到的结果以各制造单元的厚度为设计变量进行优化；得到的优化结果中，每个子部件内部的各单元板厚不一定相同，此时定义为

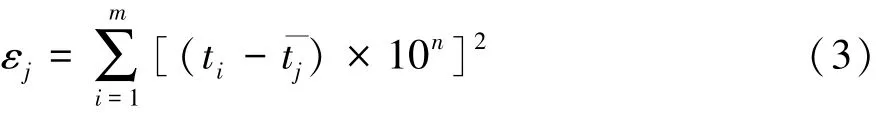
式中:εj为部件j内各单元厚度的不一致程度；tj为部件j的平均板厚。根据εj值的大小对各子部件内部的单元厚度情况进行评价:εj值大则不一致程度高，结果不好；反之则一致性高，可选取该结果进行下一步计算。式中n根据所需精度进行取值，例如图5中精度取 10－1，因此 n＝－(－1)＝ 1。 使用图分解法划定的连通域内部厚度需要约束为一致，而迭代时连通域又被重新划定，因而即使分级优化也可能会不收敛。根据合适的ε值进行筛选后，可保证各子部件内部的厚度趋向一致，提高收敛程度。

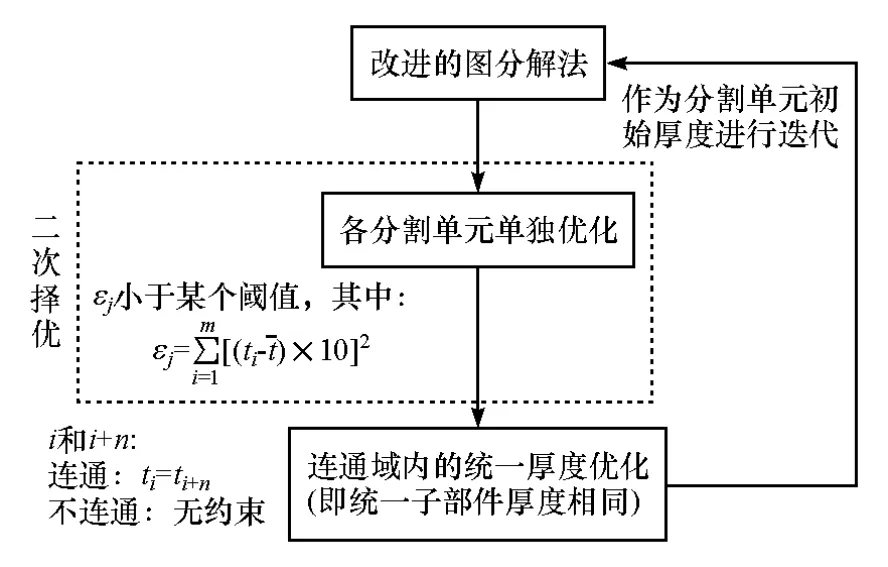
图5 二次择优算法结构

根据ε的阈值进行筛选后，对筛选出的解集施加板厚约束:连通域内(即各子部件内部)厚度保持一致。以各部件的整体厚度为优化变量进行优化，得到厚度优化结果。将该结果中各制造单元的厚度值返回到图分解算法模型中作为初始值，进行迭代计算，直至整个问题收敛。

在二次择优的过程中，初始解集(即由图分解法所得到的解集)十分重要。如果初始解集较差，可能无法选出满意的结果，导致下一次迭代无法收敛。因此，在使用图分解算法时，须将计算过程中种群的拥挤距离控制在合适的范围内:如果拥挤距离过小，则下一代解集缺少多样性[14]；如果拥挤距离过大，则下一代结果之间缺少可比性。这两种情况都将导致计算难以收敛。对于拥挤距离的相关问题，将在以后的研究中进行深入的探讨。

3 解集评优

3.1 模糊集合理论

使用进化算法对本文中问题进行优化求解时，由于涉及刚度、制造成本和装配成本等多个目标函数，优化后得到的是该代Pareto前沿曲线上的一组解集，须根据设计者的需求从终代解集中选择出一个或几个解作为优化解。本文中采用一种在工程上常用的基于模糊集合理论[15]的选优方法，可客观地得到解集中的综合性能最优解。

对解集中的每一个解，使用支配函数μk定义其综合评分，表达式为

式中:Mp为解集中解的个数；Nobj为问题中目标函数的个数。解k中的第i个目标函数值在所有解中所占的比重为

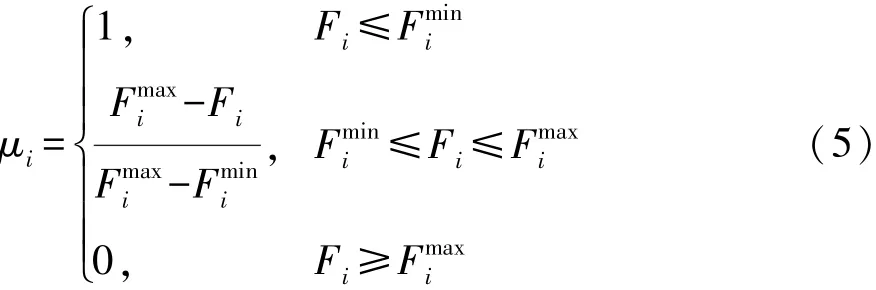
式中:为第i个目标函数值在解集中的最小值；为最大值。μi用来衡量当前解中的第i个目标函数值在整个解集中的优劣程度，μk则可用来衡量解k考虑各个目标函数后的综合性能:μk越大，其综合性能越好。因此，对解集中所有解根据其μk大小进行排序，选取μk最高的解作为最优解。

3.2 改进的评分公式

基于模糊集合理论的支配函数虽在工程领域得到了广泛的应用，但该方法仍然存在着两个明显缺陷。

(1)未考虑各个目标函数重要程度的差异。使用该公式进行评分时，各目标函数同等重要。但在实际设计过程中，设计往往需要侧重于几个重要指标。

(2)未考虑解在不同目标函数之间的均衡性。支配函数的值代表综合评分，但存在一些解，其某个目标函数值“奇高”但其他目标函数值很低，最终却由于其支配函数值较高被选为最优解。对于这种解的评价明显缺乏均衡性。

本文中针对以上这两个缺陷进行了改进，得到更为合理的支配函数表达式。首先，在原支配函数中，对解k的各目标函数单独考虑其对应权值，即

进行优化时，设计者可根据需求对权值进行实时动态调整。

考虑解k的各目标函数评分的均衡情况。由上文可知各目标函数的平均评分为函数的标准差为

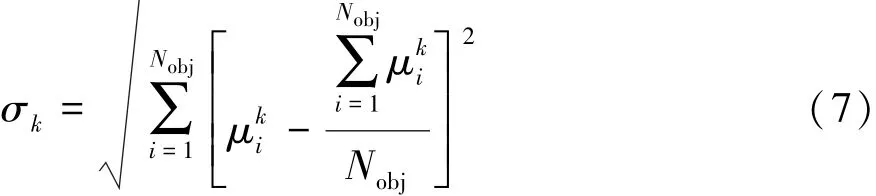
将该标准差作为一项目标函数并考虑其权值，以μi的方式加入式(4)中，得到改进的支配函数表达式为

使用式(8)对解集进行评分，可根据设计偏好选择出性能均衡的结果。

4 算例研究

4.1 算例模型

为验证方法的有效性，本文中使用某SUV车型白车身概念模型中的底板结构作为算例模型。图6为整车结构概念模型的基本结构与尺寸，模型的关键点坐标和各简化梁截面尺寸如表2所示，底板初始厚度1.2mm。模型中，梁单元尺寸30mm，网格数量4 000个；壳单元尺寸50mm，网格数量61 000个。以该模型的弯曲刚度为性能参照，图6中Load＿1和Load＿3为约束点，约束3个方向的平动自由度，Load＿2为加载点。载荷为铅直方向1 000N(对称位置存在约束点和加载点)。

表2 算例模型尺寸

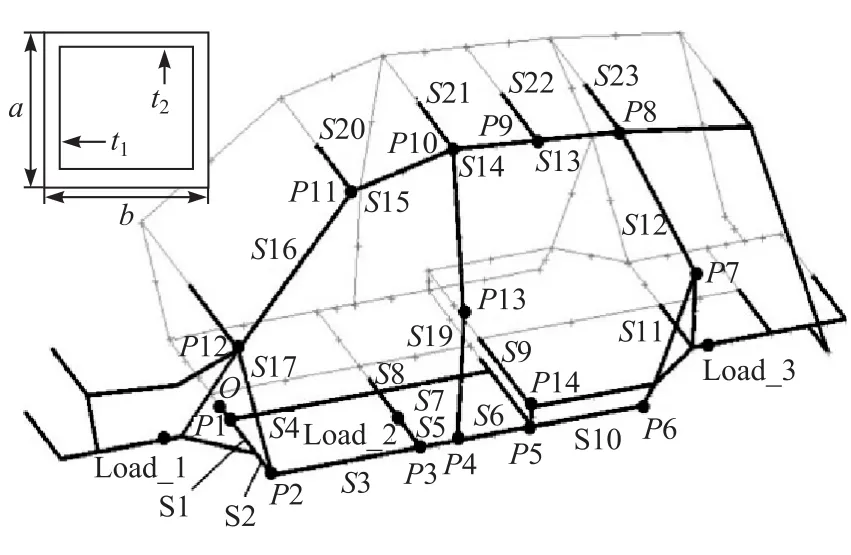
图6 简化模型示意图

优化中调用Hyperworks对模型进行计算，设置优化目标如下:

(1)车身刚度，以车身最大变形为指标，变形越大，刚度越低；

(2)制造成本，主要是模具成本，用各部件的外包络面积进行近似衡量，如图7所示，考虑到模具制造难度，总模具面积相同的个体进行比较时，模具数量越多的制造成本越低(但对应的装配成本越高)；

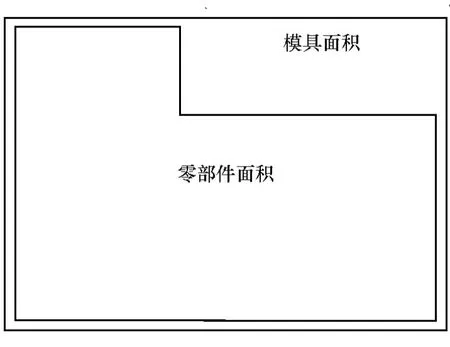
图7 部件对应模具面积示意

(3)装配成本，由于焊接为主要装配手段，用焊点个数进行近似衡量。

4.2 装配结构划分

以最小制造尺寸为单位对底板进行预分割，如图3所示。以焊缝潜在位置为设计变量进行优化，焊点以扭转弹簧进行模拟，焊接间距30mm，弹簧刚度1.0×104Nm/rad[16]。使用NSGA-II进行优化，种群规模200个，迭代终止次数100代，种群替换率50%，交叉概率90%，变异概率10%。各项数值均为多次模拟后根据收敛情况所做选择，平均适应度函数变化率小于3%时认为优化收敛。本文中考虑各项目标函数及其标准差权重相同，即认为各项指标同等重要。最终可得到优化收敛的终代种群，具有代表性的个体如表3所示。

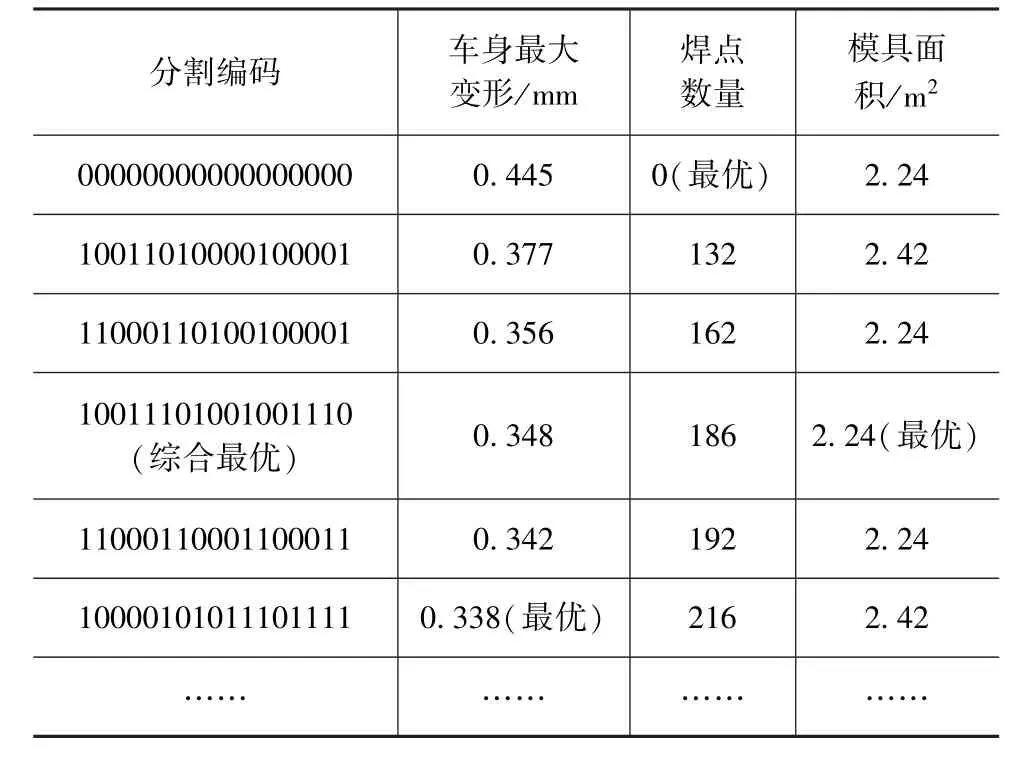
表3 相同板厚下某车身底板装配结构的一些代表性个体

4.3 二次择优及迭代结果

对得到的划分结果按照前面第2.2节的方法进行二次择优，筛选出可进行厚度优化的个体。以每个预分割单元的厚度作为优化变量，为满足工程制造需求，以0.2mm为间隔在0.8到2.2mm区间内进行离散取值。图8为一种装配设计方案，该图中以为自变量、ε为优化目标、结构的刚度和质量为约束进行优化，划分出的3块部件的ε分别为

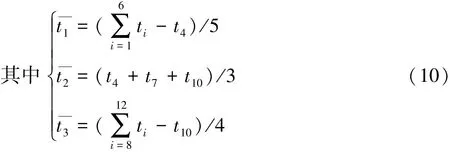
式中t 分别为3块板件的平均厚度。

如果 ε＝ε1＋ε2＋ε3小于预定阈值，则认为在保证结构性能的前提下，可对各划分后的子部件以同一板厚进行制造；否则，制造后将导致性能有较大偏差，对这样的个体应予删除。

图8 装配结构示例

仍以图8为例，对筛选出的个体的约束为

进行优化后即可得到3块子板的厚度。随后，这些优化后的个体作为初始种群，迭代回图分解法中进行装配方式的求解。

本文中设置ε为50，仍使用NSGA-II进行优化。在装配方式和板件厚度之间迭代后很快收敛，将改进的图分解法所计算的每一代群体内装配成本均值、制造成本均值和刚度均值作为纵坐标，迭代代数作为横坐标，使用MatLab输出的迭代结果折线图如图9～图11所示。每100代为一次改进图分解算法的计算周期，图中共有5个周期，可以看出，3个目标函数均在5个周期内收敛。为说明计算过程中的特征，选择终代种群中的一些代表性个体，如表4所示，这些代表性个体的装配结构、子板板厚和底板质量等如表5所示。

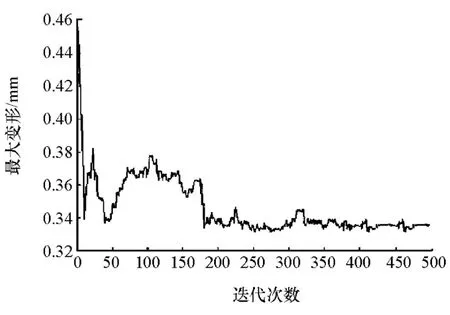
图9 迭代种群中最大位移均值变化折线图

图10 迭代种群中焊点个数均值变化折线图

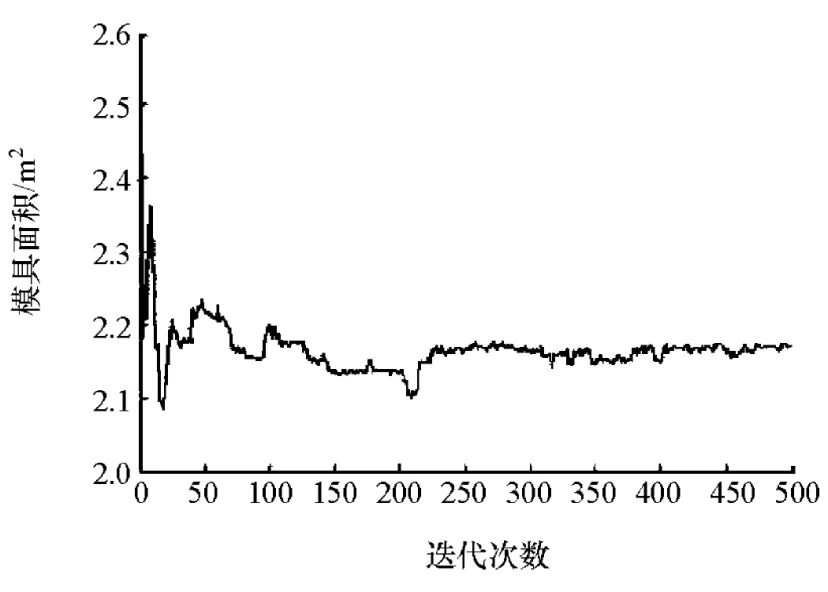
图11 迭代种群中模具面积均值变化折线图

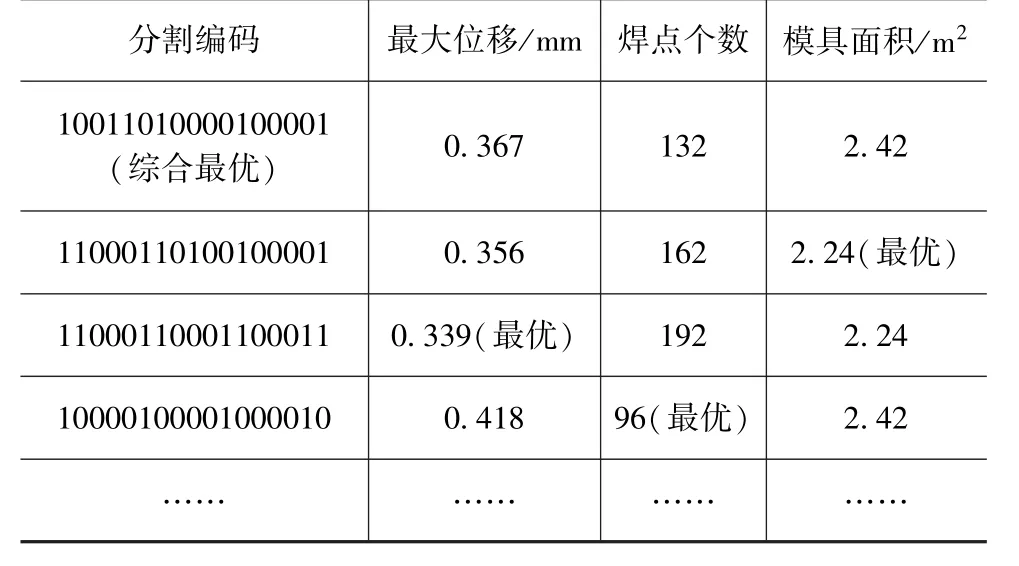
表4 最终结果种群中一些代表性个体

在计算中可以发现，最终得到的解集中很多个体并不是优化出的新结果，而是在优化过程中多次出现并一直被保留，甚至被第一次迭代的解集所包含(如表2和表3中加阴影的个体)的解，但因为其支配函数值不突出而不能被选择。可以分析，优化方法通常是在给定约束下，通过改变自变量的取值，得到目标函数最优的设计点或区域。通常这种最优对除自变量以外的其他变量是敏感的，往往不利于下一步计算或设计。对本例而言，在进行了焊缝位置的优化后，从解集中优先筛选出的结果对单元的板厚是敏感的，不利于再对板厚进行设计。本文中所提出的二次择优算法和改进的解集评分公式，实际上是改变筛选算法，将解集中适于进行下一步优化的解保留，将过于敏感的解剔除，最终得到了较为稳定的设计结果。

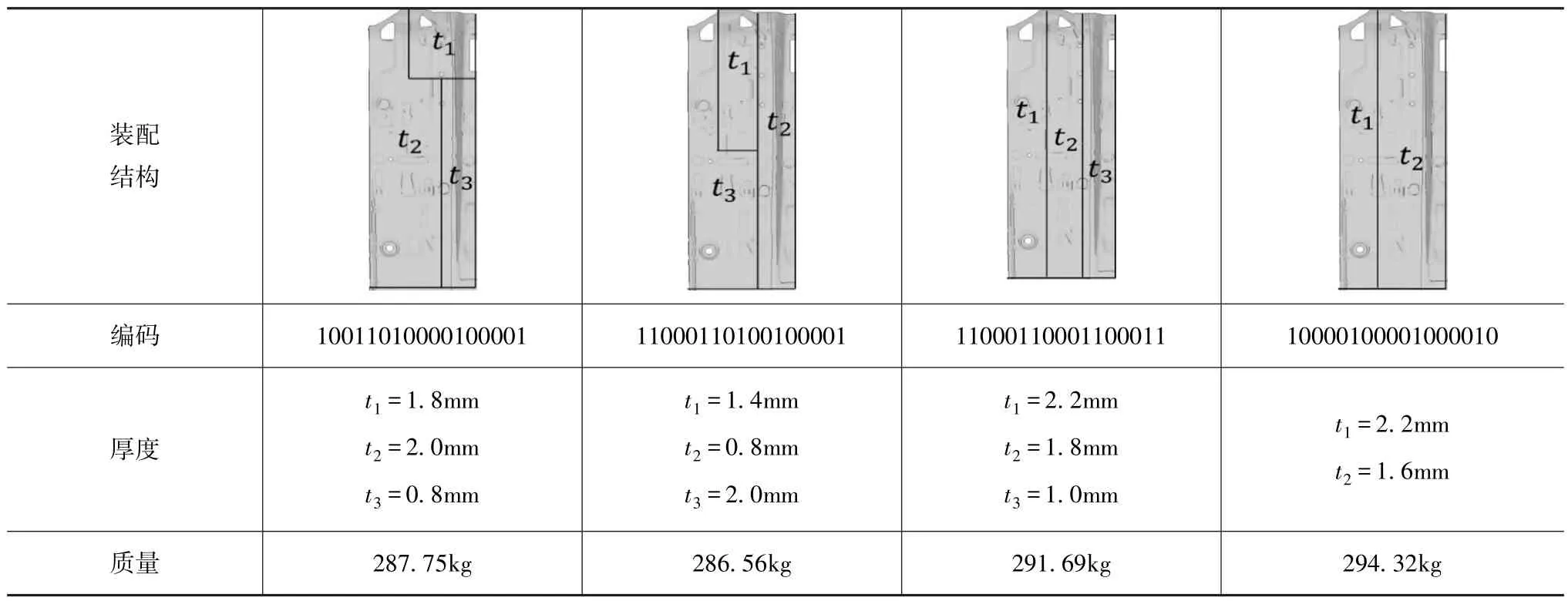
表5 终代种群中代表性个体的装配结构、板厚和底板质量

5 结论

(1)使用图分解算法可得到优化性能和成本的车身装配方式；针对考虑厚度时优化不收敛的问题，提出一种二次择优算法，实现了对焊缝位置和板件厚度的优化。

(2)将二次择优算法与图分解算法结合为多层次优化结构，求解车身装配设计的多目标优化问题，使用改进的解集评优公式得到满足设计者需求的解集，可降低车身制造成本，缩短产品开发周期，对车身研发有较好的指导意义。

(3)在计算过程中，实际上有时仍会有收敛困难的情况出现。这是因为二次择优主要是筛选种群中各板件内部厚度趋同的个体，然而对某些个体来说，板件交界位置的焊缝和厚度的变化可能会导致迭代过程中发生振荡甚至发散。在目前的研究结果中，这些情况主要出现于最优解附近，可通过人为干涉，根据需要适当修改评分公式中的权值得到解决。这个问题将在今后做进一步的研究。

[1] 黄向东，陈上华，曾庆洪，等.高拓展性模块化车身架构的研究和应用[J].汽车工程，2016，38(9):1101－1106.

[2] 王君，莫冬秀.乘用车开发平台化模块化的浅析和构想[J].装备制造技术，2014(6):154－156.

[3] 张亚萍，刘华，吴珩晓，等.浅析汽车平台演进与模块化战略[J].汽车工业研究，2015，01:27－31.

[4] 高云凯.汽车车身结构分析[M].北京:北京理工大学出版社，2006.

[5] ASHLEY S.Steel cars face a weighty decision[J].Mechanical Engineering，1997，119(2):56－61.

[6] 赵荣远.汽车虚拟装配技术及其可装配性评价分析[J].上海汽车，2013(3):45－49.

[7] 佟振博，孙朝阳，王刚，等.面向工程系统研制的可制造性评价策略研究[J].计算及集成制造系统，2005，11(10):1461－1464.

[8] HOU Wenbin， SHAN Chunlai， YU Ye， et al.Modular platform optimization in conceptual vehicle body design via modified graphbased decomposition algorithm and cost-based priority method[J].Structural and Multidisciplinary Optimization，2017，55:2087 －2097.

[9] 王江涛，戴国洪，朱林立.基于分层理论和连接关系的装配结构树自动快速生成研究[J].机械设计，2012，29(10):15－19.

[10] 付宜利，田立中，谢龙，等.基于有向割集分解的装配序列生成方法[J].机械工程学报，2003，39(6):58－62.

[11] 蔡伟，张桂香.基于成本和并行装配序列有向图求解[J].微计算机信息，2012，28(2):22－24.

[12] 侯文彬，侯大军，徐金亭，等.基于车身装配结构优化的改进图分解算法[J].应用数学和力学，2015，36(5):515－522.

[13] 刘中华，张颖超.深度优先搜索的非递归算法[J].科技信息，2010(25):160－162.

[14] DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multi-objective genetic algorithm:NSGA-II[J].Evolutionary Computation， IEEE Transactions on，2002，6(2):182－197.

[15] ABIDO M A.Multi-objective evolutionary algorithms for electric power dispatch problem[J].IEEE Transactions on Evolutionary Computation，2006，10(3):315－329.

[16] 迟瑞丰，侯文彬，胡平.接头在车身结构概念设计阶段对刚度的影响[J].机械设计与制造，2009(11):180－181.