基于多模型交互的复杂工况下车辆状态估计∗

刘 刚，靳立强

(1.吉林大学，汽车仿真与控制国家重点实验室，长春 130025； 2.河南工学院，新乡 453000)

前言

车辆电子稳定控制系统(electronic stability program，ESP)是无人车的重要组成部分。车辆在行驶中的多个状态参数诸如质心侧偏角、轮胎侧向力等均因硬件成本过高而采用参数估计的方法来降低成本。参数估计的准确性会影响车辆稳定性控制的效果，质心侧偏角被用来作为ESP控制器的控制变量，控制器能够根据质心侧偏角来判断车辆在转向过程中是否发生偏离轨迹出现失稳的情况；ESP控制器在进行直接横摆力矩控制时，则须依据轮胎受力情况进行横摆力矩分配。因此准确实时辨识出车辆行驶状态参数有助于提高车辆稳定控制系统的鲁棒性[1－3]。

国内外学者针对车辆行驶状态参数做了大量的研究。文献[4]中采用3个卡尔曼子滤波器分别对横向车速、质心侧偏角等参数进行估计，再将初步估计的结果送入主滤波器中进行数据融合，最终获得车辆状态参数，并通过实车实验证明了该方法的有效性。文献[5]中采用传感器测量车辆的轮速、加速度，然后根据动力学理论进行质心侧偏角的初步估计，配合GPS导航仪进行数据校正，保证了质心侧偏角的准确性。文献[6]中采用带遗忘因子最小二乘法估计车辆轮胎的侧偏刚度，将其输入至非线性观测器中估计质心侧偏角。文献[7]中采用变结构扩展卡尔曼滤波作为估计算法，考虑到因路面附着系数造成参数估计的误差较大，采用了质心侧偏角反馈补偿的方法保证了参数估计的准确性。文献[1]和文献[8]～文献[11]中分别使用了龙贝格观测器、滑模观测器、鲁棒观测器和伪积分数据融合等方法进行参数估计，并进行了软件仿真。

分析上述文献得知，参数估计所用的车辆模型会影响参数估计的准确性和实时性。车辆行驶过程中会经历多种路况，在极限工况下，轮胎侧偏特性会从线性转变为非线性。在具有较大的侧向加速度的工况下，车辆模型应采用非线性轮胎模型，这样能准确地反映车辆的当前状态。如果在极限工况下车辆模型中采用线性轮胎模型，则会因轮胎模型误差而造成参数估计不准确。当然，在普通工况下，应采用线性轮胎模型，这样能保证参数估计算法具有小计算量和实时的特点。本文中采用多模型交互(IMM)的方法，根据车辆行驶状态的不同切换车辆模型中的轮胎模型，在IMM算法中引入SRCKF算法进行参数估计。同时，以车辆侧向加速度和路面附着系数为模糊因子，采用模糊算法对模型切换概率进行修正，保证了算法在不同工况下的切换速率。整个算法结构如图1所示。

1 车辆模型

1.1 车辆模型

图2示出传统乘用车的7自由度车辆模型，它包括了纵向、侧向、横摆方向和车辆4个车轮的运动方程。式(1)～式(3)分别为车辆纵向运动方程、侧向运动方程和横摆方向运动方程。

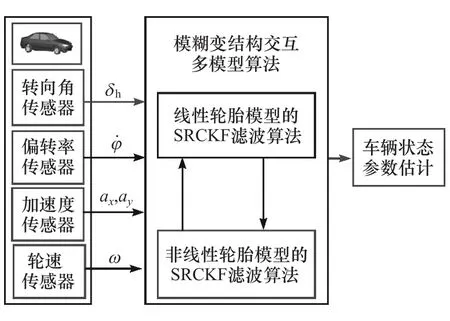
图1 车辆状态参数估计结构图

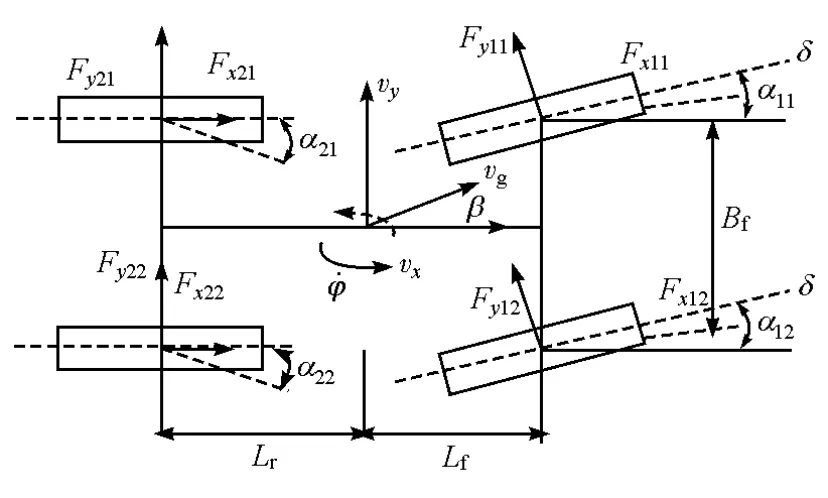
图2 车辆模型

式中为车辆模型中轮胎的纵向力的和；为轮胎侧向力的和；∑Mz为横摆力矩的和；vx和vy分别为车辆的纵向速度和侧向速度；φ·为横摆角速度；β为质心侧偏角；δ为前轮转角；m为车辆质量；Izz为惯性变量；Lf和Lr分别为前轴和后轴距质心的距离。

车辆在受到侧向加速度或纵向加速度作用时，轮胎在垂直于地面方向的力会发生变化，因此轮胎在垂直于地面的运动方程为

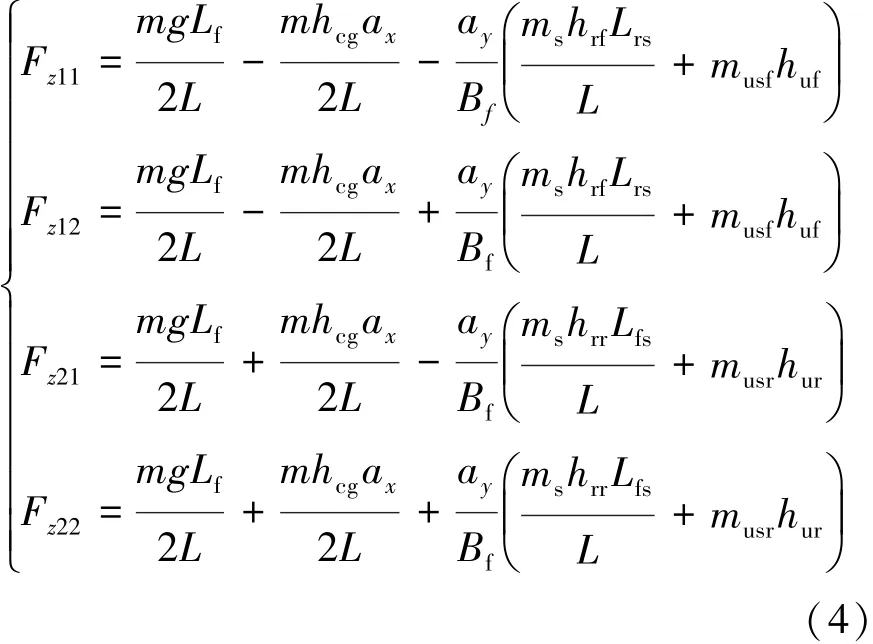
式中:ax和ay分别为车辆的纵向加速度和侧向加速度；musf和musr分别为车辆前后簧载质量；hcg为簧载质心和车辆质心之间的高度差。

1.2 轮胎模型

由文献[12]可知，轮胎模型的精度决定了车辆状态参数估计的准确性，在侧向加速度大于0.4g时，轮胎模型会逐渐表现出非线性的特点。图3示出了车辆在不同工况下侧偏角与轮胎侧向力之间的关系[13]。在正常工况下，车辆轮胎侧偏角较小，且和轮胎侧向力之间为线性关系；当车辆在复杂工况下，车辆侧偏角逐渐增大时，侧偏角和侧向力之间的关系会变成非线性，这是由于车辆的侧偏刚度在复杂工况下不再成线性变化而造成的[14]。结合上述分析，本文中考虑在估计车辆状态参数时，采用根据工况切换线性轮胎模型和非线性轮胎模型的方法。考虑到如采用单一的卡尔曼滤波方式针对两种不同轮胎模型进行参数估计时，两种轮胎模型测量噪声的协方差矩阵不同，且单一的滤波算法不能有效地进行模型切换可能会造成滤波发散的情况。因此在模型切换方面，采用交互多模型(IMM)法解决这一问题，IMM是通过多个子模型描述目标的运动状态，多个子模型单独进行滤波估计，模型之间的切换主要是服从马尔科夫过程，IMM算法目前已在航空、航天多领域中广为应用[15]。

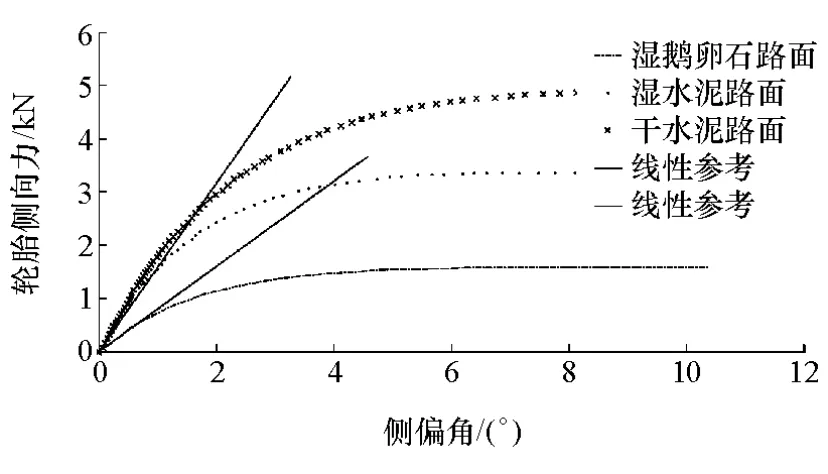
图3 车辆侧偏角与轮胎侧向力的关系

1.2.1 线性轮胎模型

轮胎侧向力和侧偏角成线性关系时，轮胎纵向受力和侧向力分别为

1.2.2 非线性轮胎模型

当轮胎侧向力和侧偏角成非线性关系时，根据Dugoff轮胎模型可改写为

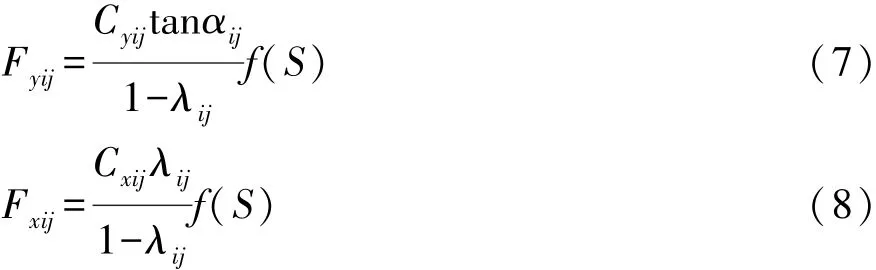
2 估计算法设计

2.1 IMM-SRCKF

本文中设计的IMM算法由两个滤波器构成，两个滤波器的模型分别是以线性轮胎模型为基础的7自由度车辆模型和以非线性轮胎模型为基础的车辆模型，针对两个模型分别采用SRCKF，这两个模型之间转换则是由IMM依据马尔科夫矩阵即历史先验信息决定的。IMM算法是递推算法，它得到参数估计结果是两个模型SRCKF滤波器状态估计值的加权和。

步骤1 输入交互

此步骤主要是为了对上一时刻(k－1时刻)两个滤波器输出的参数估计值进行加权融合，并作为当前时刻的输入初值。k－1时刻的混合权值为

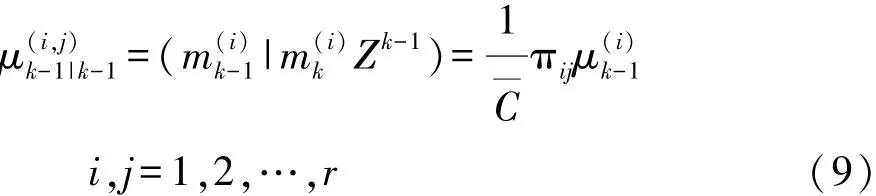
经过交互计算得到k时刻的输入初值，即状态与协方差矩阵为

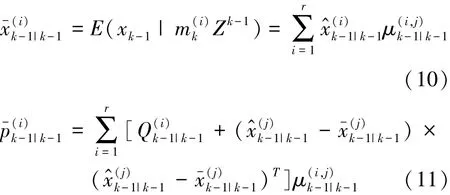
步骤2 SRCKF算法

在得到k时刻的初值后，在步骤2采用SRCKF算法进行两个模型的状态更新，即得到两个模型的状态估计值和误差协方差矩阵在步骤2中涉及到了SRCKF算法。

根据式(1)～式(6)改写的基于线性轮胎模型的车辆状态方程和根据式(1)～式(4)，式(7)和式(8)改写的基于非线性轮胎模型的车辆状态方程均可表示为

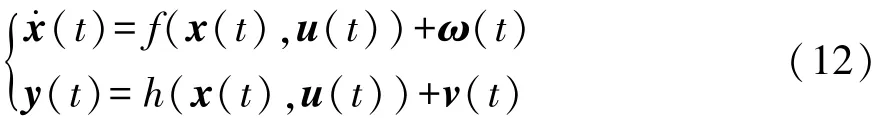
式中:u 为输入矩阵，u＝[δh，ω11，ω12，ω21，ω22]；y 为车辆模型系统的量测输出矩阵，y＝ [ax，ay，，ω11，ω12，ω21，ω22]，矩阵中的各个元素均可通过传感器测量，其中ax和ay可采用双轴加速度传感器测量，通过偏航率传感器测量，ω通过轮速传感器测量；x为状态矩阵，x＝[，β，Fy11，Fy12，Fy21，Fy22，Fx11，Fx12，Fx21，Fx22]。

SRCKF算法可参见文献[15]。

步骤3 模型概率更新

假设两个模型的滤波残差均服从高斯分布，则似然函数为

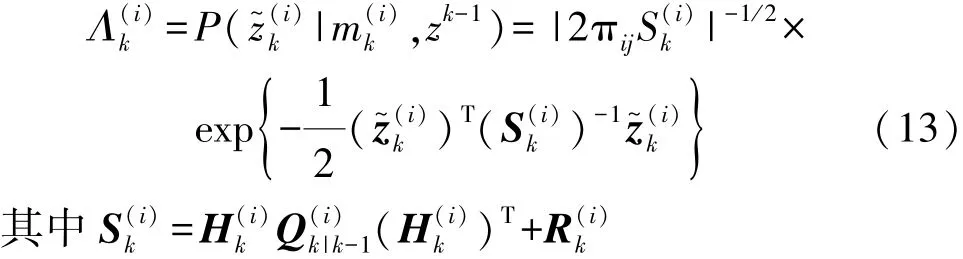
在此步骤得到的IMM算法中的模型概率更新为

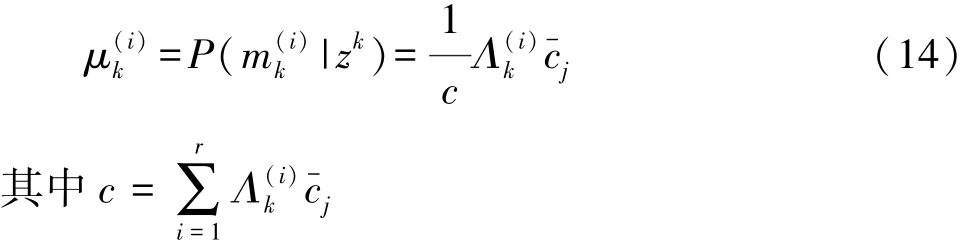
步骤4 估计融合

在此步骤下，可以得到当前时刻(k时刻)的状态估计和协方差矩阵为

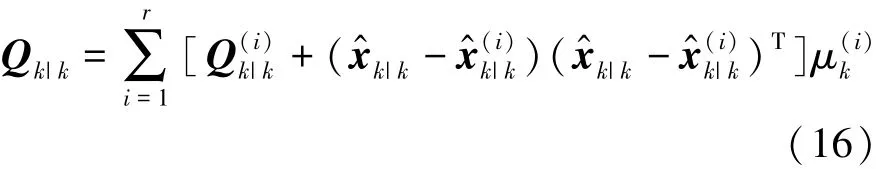
2.2 修正的IMM

在标准的IMM算法步骤3模型概率更新部分，模型之间跳变是由马尔科夫矩阵决定的，而马尔科夫矩阵的值是滤波之前就已经被确定下来。考虑到车辆行驶的工况是复杂多变，依靠先验数据的马尔科夫矩阵不能实时反映车辆当前行驶工况，因此本文对IMM算法的步骤3模型概率更新部分进行修改，图4示出修正的IMM算法结构框图。

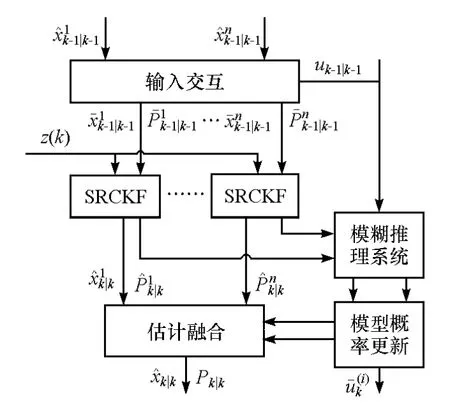
图4 修正的IMM-SRCKF算法结构图

车辆在转弯过程中侧向加速度反映了轮胎和地面附着稳定程度。如在高附着路面上，侧向加速度小于0.4g时，车辆轮胎侧偏特性处于线性区间；大于0.4g时会变成非线性，最终会出现极限失稳的情况[14]。在不同的附着系数下，侧向加速度在线性区间的极值不同。因此本文以侧向加速度和路面附着系数作为权值对模型概率更新进行修正。两个模型更新概率分别修正为 f(ay/uf－e)μ(i)k和[1－f(ay/uf－e)]μ(i)k。 式中:uf－e为路面附着系数；ay为测得的侧向加速度；μ(i)k为在k时刻模型i的更新概率。

因两个模型更新概率之和为1，故须对修正值进行归一化处理才能最终得到模型更新概率，再代入至IMM算法的步骤4中计算k时刻总体估计和误差协方差矩阵。

在此修正部分，f(ay/uf－e)的值是采用模糊算法作为模糊权重函数的输入值。当较小时表示侧偏特性尚处于线性区间，此时f(ay/uf－e)相应较小，表示采用线性轮胎模型的概率值较大逐渐增大，车辆的侧向加速度超过0.4g时会导致车辆极易失控，此时对IMM算法中的轮胎模型切换概率进行修正，非线性轮胎模型的概率值较大。图5和图6所示为函数。

图5 输入变量的隶属度函数

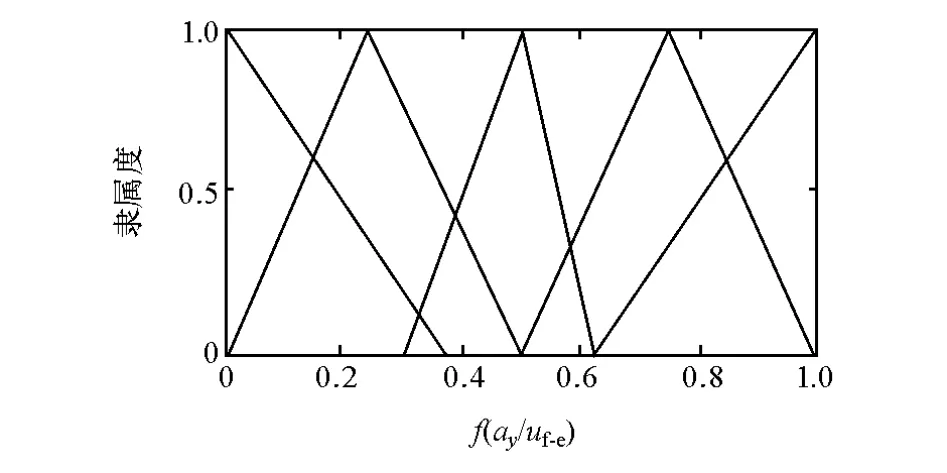
图6 输出变量的隶属度函数

3 仿真和分析

为验证本文中提出的车辆状态参数估计算法，进行Carsim和Matlab/simulink联合仿真，仿真方案如图7所示。估计算法在Matlab/simulink中实现。仿真工况为双移线，车辆速度70km/h，转向盘转角最大值达到55°，侧向加速度达到0.5g左右，路面附着系数设为0.35。运行Carsim时，车辆按照设置工况行驶，行驶过程中将车辆的转向盘转角、横摆角速度、纵向加速度、横向加速度和轮速信号传输至Matlab/simulink所建的车辆状态估算算法中进行状态估算。

图7 Carsim和Matlab/simulink联合仿真示意图

仿真结果如图8所示，图中同时示出采用IMMCKF(interacting multiple model-cubature kalman filter)[15]算法的仿真结果。由图可见，本文中提出的车辆状态估计算法能较准确地跟踪实际状态，出现的误差较小，该误差是由算法采用的车辆模型忽略了悬架以及载荷转移造成的。而IMM-CKF算法的仿真结果则与车辆实际状态在4.5～5.3s和6～7.3s这两个时间段出现较大误差，因为此时车辆的侧向加速度逐渐增大，轮胎的侧偏特性开始由线性向非线性过渡，而IMM-CKF算法在模型切换时无法根据外部工况及时进行调整而造成的。本文中提出的算法耗时为0.2ms，比IMM-CKF算法缩短24%。

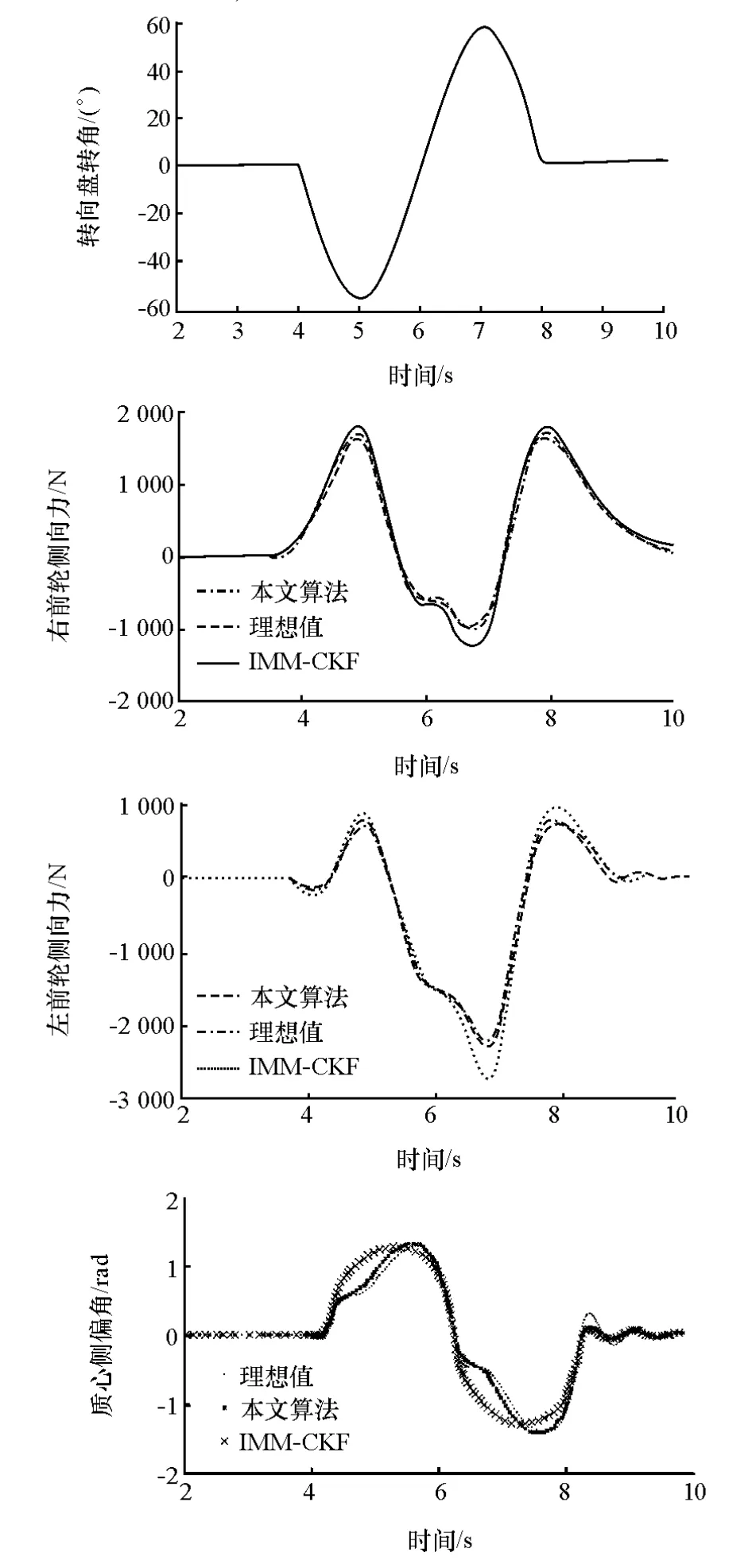
图8 仿真结果对比

由仿真结果可知，本文中提出的算法跟踪精度高，模型切换更快更合理，鲁棒性和实时性更好。这是因为IMM-CKF算法中，CKF须在每次迭代运算时进行矩阵分解，而本文算法采用的SRCKF则直接用协方差矩阵的平方根进行递推运算，提高了实时性和算法的鲁棒性。

4 实车试验

2015年12月在黑河红河谷试车场进行了实车试验，车型为一汽生产的某型轿车。车辆安装了Corrsys-datron的S400质心侧偏角光学传感器和S-32轮胎侧向力传感器。车辆的控制器采用恩智浦的单片机MPC5604，搭载实时操作系统OSEK Turbo OS，保证了单片机的实时性要求。整个算法单次运行耗时0.5ms。本次主要是在冰雪路面上进行双移线工况试验，附着系数为0.3，车速40km/h，侧向加速度最大达到0.55g，全程无制动。试验结果如图9所示。

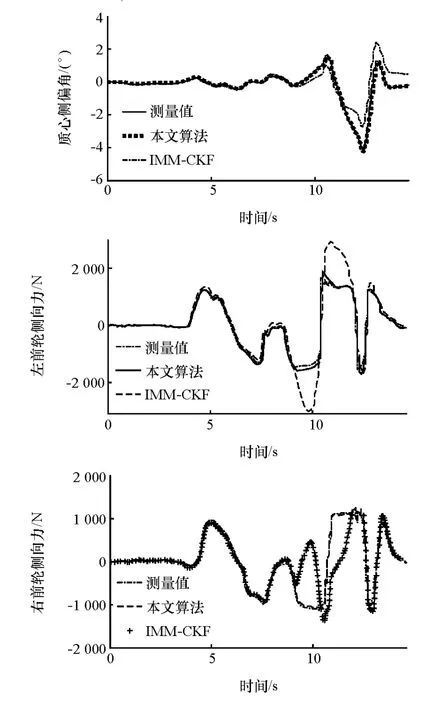
图9 实车试验数据

由图可见，本文算法对侧向力和质心侧偏角的估计值能密切跟踪传感器测量值；而IMM-CKF算法的估计值跟踪性能较差。在10～14s时，车辆侧向加速度逐渐增大，轮胎侧偏特性转变为非线性的过程中，由于IMM-CKF算法未能根据车辆当前状态及时切换模型，所以10～14s之间估计值误差较大。本文中所提算法对侧向力和质心侧偏角的估计值跟踪性能良好，较能反映真实值。由图还可看出，由于试车场地雪路面不平造成传感器采集数据中噪声过大，所以两种算法估计值均有波动，但本文提出的算法波动较小。

5 结论

本文中分别建立了基于线性轮胎模型的车辆运动模型和基于非线性轮胎模型的车辆模型，采用IMM-SRCKF算法对车辆状态参数进行估计。在该算法中考虑到侧向加速度、路面附着系数对参数估计影响较大，所以在IMM递推运算过程中加入修正值，该修正值与侧向加速度和路面附着系数相关。通过仿真和冬季实车试验结果证明了该算法的有效性。

通过试验数据对比发现，本文中算法在参数估计精度方面有些小误差，该误差可能是由于车辆在行驶过程中载荷转移造成的。下一步工作有两方面，分别是车辆在不同载荷下和ESP控制介入下车辆状态参数的准确估计。

[1] BOADA B L， BOADA M J L， DIAZ V.Vehicle sideslip angle measurement based on sensor data fusion using an integrated ANFISand an unscented Kalman filter algorithm[J].Mechanical Systems and Signal Processing，2015，36(3):713－720.

[2] BOADA B L，BOADA M JL，G A A，et al.Sideslip angle estimator based on ANFISfor vehicle handling and stability[J].Journal of Mechanical Science and Technology，2015，29(4):1473－1481.

[3] ZHANG H， HUANG X， WANG J， et al.Robust energy-to-peak sideslip angle estimation with applications to ground vehicles[J].Mechatronics，2015，30(7):338－347.

[4] 高博麟，陈慧，陈威，等.汽车质心侧偏角融合估计方法[J].汽车工程，2013，35(8):716－720.

[5] LI X，SONG X，CHAN C.Reliable vehicle sideslip angle fusion estimation using low-cost sensors[J].Measurement，2014，51(7):241－258.

[6] LIAN Y F，ZHAO Y，HU L L，et al.Cornering stiffness and sideslip angle estimation based on simplified lateral dynamic models for four-in-wheel-motor-driven electric vehicles with lateral tire force information[J].Int JAuto Tech-Kor，2015，16(4):669－683.

[7] LIL，JIA G，RAN X，et al.A variable structure extended Kalman filter for vehicle sideslip angle estimation on a low friction road[J].Vehicle System Dynamics，2014，52(2):280－308.

[8] 武冬梅，丁海涛，郭孔辉.基于线性估计模型的电动汽车质心侧偏角估计[J].吉林大学学报(工学版)，2014，44(4):901－910.

[9] 朱绍中，余卓平.极限行驶条件下车辆质心侧偏角观测器设计[J].同济大学学报，2009，37(8):1070－1078.

[10] VENHOVENSP J T H，NAAB K.Vehicle dynamics estimation using Kalman filters[J].Vehicle System Dynamics，1999，32(2－3):171－184.

[11] GRIP H F，IMSLAND L，JOHANSEN T A，et al.Nonlinear vehicle side-slip estimation with friction adaptation[J].Automatica，2008，44(3):611－622.

[12] SHIBAHATA Y，et al.Improvement of vehicle maneuverability by direct yaw moment control[J].Vehicle System Dynamics，1993，22(5－6):465－481.

[13] BAFFETG，CHARARA A，LECHNERD，et al.Experimental evaluation of observers for tire-road forces，sideslip angle and wheel cornering stiffness[J].Vehicle System Dynamics，2008，46(6):501－520.

[14] CHELIF，SABBIONIE，PESCE M，et al.A methodology for vehicle sideslip angle identification:comparison with experimental data[J].Vehicle System Dynamics，2007，45(6):549－563.

[15] CUI N，HONG L，LAYNE JR.A comparison of nonlinear filtering approaches with an application to ground target tracking[J].Signal Processing，2005，85(8):1469－1492.

[16] LEE H.Reliability indexed sensor fusion and its application to vehicle velocity estimation[J].Journal of Dynamic Systems，Measurement， and Control，2006，128(2):236.