某新型线控转向系统的自适应模糊滑模控制∗

陈辛波，罗 杰，杭 鹏，方淑德，罗凤梅

(1.同济大学汽车学院，上海 201804； 2.同济大学新能源汽车工程中心，上海 201804)

前言

相对传统转向系统，线控转向系统主要具有以下优势:取消了转向杆系，提升了车辆的被动安全性；转向电机能实现更大的车轮转角，反馈电机提供了更好的“路感”。

线控转向系统常用PID控制，但由于转向系统外部扰动和系统不确定性的存在，PID控制难以满足鲁棒性要求[1－3]。因此，简单、鲁棒性好、可靠性高的滑模控制，逐渐被运用于线控转向系统[4－6]。然而，传统的滑模控制须预知系统外部扰动，而且容易引入抖振。针对此问题，一些学者提出利用自适应控制、自学习控制和模糊控制等控制理论对系统外部扰动进行估计，取得了一定的降低抖振的效果，但需要人为选定的控制参数比较多[7－9]。

本文中提出一种无需预知系统扰动的精确界、并能降低抖振现象的自适应模糊滑模控制方法，并验证了该方法的有效性。

1 新型线控转向系统构型

一种自主研发的基于烛式悬架的线控转向系统如图1所示，该系统同时集成了悬架系统和驱动系统。上滑柱8与减速器5输出轴相连，下滑柱14与制动盘3相连并作为转向节。上、下滑柱8和14之间通过圆柱副相连，从而实现悬架的跳动。上、下滑柱8和14之间的转矩通过上摆臂9和下摆臂12传递。转向电机7产生的转矩经由减速器5、上滑柱8、上摆臂9、下摆臂12和下滑柱18最后传至车轮1。转角传感器6可实时测量转角信号。一款自主研发的装配了该线控转向系统的四轮独立转向电动汽车(4WISEV)如图2所示，整车参数如表1所示。

图1 一种新型线控转向系统

图2 四轮独立转向电动汽车

表1 整车参数

2 系统建模

2.1 线控转向系统动力学建模

该线控转向系统简化模型如图3所示。

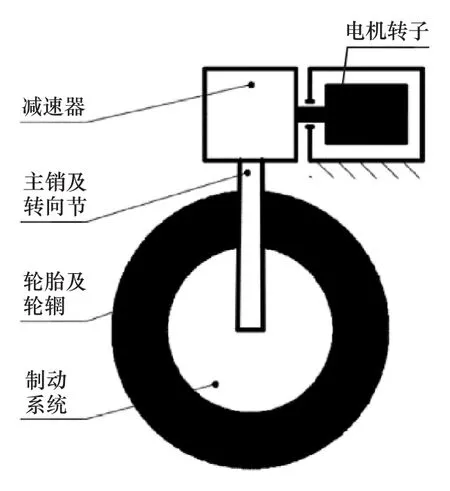
图3 线控转向系统简化模型

电机转子的动力学方程为

式中:Jm为电机转子转动惯量；δm为电机转子转动角度；Bm为电机黏滞摩擦因数；Tw2m为车轮作用在转向电机上的转矩；Tm为电机产生的转矩；Tctr为控制转矩；ΔTpert为电机扰动。

转向轮动力学方程为

式中:Jw为车轮转动惯量；δw为车轮转动角度；Bw为车轮黏滞摩擦因数；TF为库仑摩擦力矩；Te为回正力矩；Tm2w为转向电机给车轮的转矩。

k为减速器的减速比，可得

根据式(1)、式(3)和式(4)，可得到线控转向系统的动力学方程:

式中:Jeq为系统等效转动惯量；Beq为系统等效黏滞摩擦因数；Teq为作用在系统上的等效转矩；Tl为总扰动转矩。

结合式(6)和式(7)，线控转向系统动力学方程可表示为状态空间形式:

2.2 系统扰动分析

根据式(7)，总扰动Tl由回正力矩Te、库仑摩擦力矩TF和电机扰动ΔTpert组成。

针对具体悬架结构，主要考虑由侧向力引起的回正力矩:

式中:lc为轮胎机械拖距；lp为气胎拖距；Fyi为侧向力；Ci和αi为轮胎侧偏刚度和轮胎侧偏角；下标i表示前轮(f)或者后轮(r)。当车辆质心侧偏角β很小和侧向速度v变化缓慢时，有

式中:lf为质心到前轴距离；lr为质心到后轴距离；ω为横摆角速度。

库仑摩擦力矩TF为

式中:Fs为库仑摩擦常数。

转向电机为无刷直流(BLDC)电机，其输出转矩与相电流成正比[10]，可简化为

式中:Kt为电机常数；I为相电流。电机输出扰动可等效为Kt和I的扰动，式(14)可表示为

式中ΔKt和ΔI分别为Kt和I的扰动量。故电机扰动可表示为

总扰动Tl仅在仿真中作为验证控制器鲁棒性的外界输入，而不作为控制器的输入。

3 自适应模糊滑模控制器设计

3.1 传统滑模控制器设计

基于系统动力学模型，本节中先给出传统滑模控制器的求解过程。式(8)可表示为

U(t)＝Tm

式中D(t)为扰动矩阵。

转角跟踪误差为

式中Xref＝[δref]T，δref为参考转角。

滑动参数定义为

式中 K＝[λ 1]T，λ＞0。 可得

控制律U由等效控制项Ueq和切换项Us构成:

式中η为切换常数，η＞0。

滑动阶段，即s＝0时，利用等效控制项Ueq可保证系统动态在滑动面上滑动。Ueq可以通过方程s·＝0求解。到达阶段，即s≠0时，通过合理设计切换项Us，使系统满足式(23)滑动条件，从而使系统动态能趋近于并最终停留在滑模面s＝0上[11]。

将式(22)代入式(20)，可得

取η≥‖KD‖时，式(22)滑动条件成立。

为获得传统滑模控制的控制律，需要先确定切换常数η。根据式(25)，当KD较大时，要求选取较大的η，这将导致严重的抖振，而且使系统保守性过大。为了减小抖振和降低系统保守性，应使切换项在保证鲁棒性的前提下尽量小。然而，KD中包含扰动项D，其精确界难以获得。

3.2 自适应模糊滑模控制器设计

传统的滑模控制需预知系统扰动的精确界，本节将利用一个模糊系统对系统扰动进行估计。该模糊系统的输入为滑动参数s，输出为ηsgn(s)的估计值h＾。根据隶属度函数的设计程序[12]，设计了合适的隶属度函数，如图4所示。

图4 s的隶属度函数

模糊系统输出为

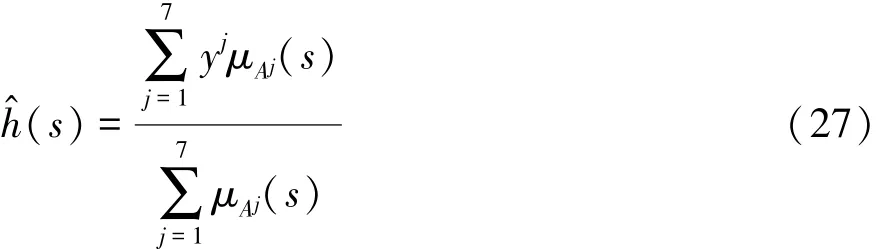
式中:μAj(s)为s的隶属度函数；yj为隶属度函数取得最大值时所对应的ηsgn(s)的值，其值可通过自适应律实时调节。

引入模糊基向量ϕ(s)，式(27)可表示为

其中:θh＝[y1… y7]T

ϕ(s)＝[φ(s)1… ϕ(s)7]T

θh通过自适应律确定:

式中γ为自适应参数，且γ＞0。

用 h＾替换式(21)中的 ηsgn(s)，得

此时，滑动条件为

3.3 渐进收敛性分析

定理1:针对式(17)系统，若运用式(30)控制律，其中 h＾由式(27)给定，θh由式(29)给定，那么，此闭环系统有界，而且其跟踪误差渐进收敛于0。

证明:设θh的最优参数为

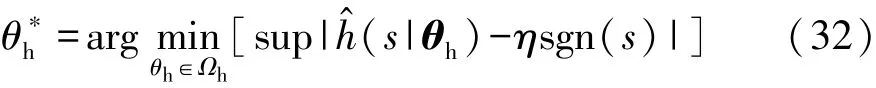
式中Ωh为θh的集合。ηsgn(s)可以表示为

式中 ε 为模糊系统的估计误差，｜ε｜≤εN，εN＞0。

将式(33)代入式(24)，得

选取李雅普诺夫方程为

微分可得

将式(34)代入式(37)，可得

将式(33)和式(35)代入式(38)，可得

取 η≥｜KD｜＋εsup，εsup为估计误差上界，则

当≡0，s≡0时，由拉塞尔不变性原理可得，当时间 t→∞时，s→0。

4 仿真与结果

为验证AFSMC控制器的性能，设计了一个工程中常用的PID控制器。该PID控制器的负反馈信号为转角跟踪误差，其参数通过粒子群法(PSO)寻优获得:kP＝297，kI＝21 和 kD＝102，kP，kI和 kD分别为比例、积分和微分增益，闭环系统内部稳定。

整车参数和线控转向系统参数见表1和表2，电机的最大转矩为±3.85N·m，电机常数和相电流的摄动各设为5%，自适应参数γ＝1.5，仿真采样时间为0.001s。

表2 线控转向系统参数

4.1 正弦参考信号输入仿真

为验证AFSMC的跟踪性能、鲁棒性能和能效性能，给定前轮转角的参考转角信号为

后轮转角信号始终为 0，初始前轮转角为－0.15rad。假设前后车轮侧偏刚度时变:

转角跟踪性能如图5(a)所示，相对传统的PID控制，AFSMC无超调量、响应更快。从图5(b)可以看出，AFSMC的跟踪误差更小。从图5(c)可以看出，滑模变量在0.16s时稳定在了0附近，说明AFSMC能使滑模变量快速收敛。总扰动如图5(d)所示。从图5(e)可以看出，sh＾一直大于s KD，即仿真过程中式(31)滑动条件一直成立。从图5(f)可以看出，AFSMC所需控制力矩更小，降低了对转向电机峰值转矩的要求，同时AFSMC较好地抑制了抖振问题。从图5(g)可以看出，AFSMC所需的控制功率更小，有利于整车的能效。

4.2 单变道/双变道仿真

为实现前文所述4WISEV的路径跟踪能力，开发了一套以μ综合鲁棒控制为主环、AFSMC为伺服环的整车控制策略，具体结构如图6所示。首先将目标路径的曲率输入给μ综合鲁棒控制器，之后μ综合鲁棒控制器计算出前轮和后轮的参考转角，再将参考转角输入给AFSMC控制器进行跟踪，最后将整车状态和各转向系统状态进行反馈。受限于文章篇幅，4WIS EV建模和μ综合鲁棒控制器求解过程不再详述。

图6 4WISEV整车控制策略

为验证结合AFSMC的整车控制策略的路径跟踪性能，进行了单变道仿真，车速为20m/s，结果如图7所示。

图7 (a)说明在不考虑扰动时，结合AFSMC的整车控制策略和结合PID控制的整车控制策略都能较好跟踪目标路径。考虑扰动时，结合AFSMC的整车控制策略能较好地跟踪目标路径，而结合PID控制的整车控制策略出现了失稳现象，因而图中未给出。图5(b)和图5(c)说明了不管考虑扰动与否，AFSMC都能很好地跟踪目标转角。图5(d)说明PID控制出现了强烈振荡，因此所述PID控制器不适合在实际场合中使用。

为进一步验证结合AFSMC的整车控制策略的路径跟踪性能，进行了双变道仿真，车速为25m/s，结果如图8所示。图(8)说明了不管考虑干扰与否，结合了AFSMC的整车控制器都能较好地实现路径跟踪，同时可以看出干扰对路径跟踪性能影响很小。

5 结论

本文中首先提出了一种创新的线控转向系统构型，进而提出针对此线控转向系统的自适应模糊滑模控制，该控制具有无需预知系统扰动精确界和能降低抖振现象的特征。

正弦参考信号输入的仿真结果显示，AFSMC控制下的线控转向系统具有良好的转角跟踪性能、鲁棒性能和能效性能。为验证AFSMC在整车控制策略中的性能，针对所述的4WIS EV设计了一套以μ综合鲁棒控制为主环、AFSMC为伺服环的整车控制策略。单变道和双变道工况的仿真结果显示，不管考虑扰动与否，作为整车控制策略的伺服环，AFSMC较好地完成了目标转角的跟踪，进而实现了整车的路径跟踪。

[1] 余颖弘，王保华.汽车线控转向实验台转向驱动系统的辨识及其PID控制[J].湖北汽车工业学院学报，2016，30(2):1－4.

[2] 李珊，谭光兴，林川.基于模糊PID线控转向系统前轮转角控制[J].广西科技大学学报，2012，23(3):56－60.

[3] FU X，LI F，FENG K.Research of automotive steer-by-wire control based on integral partition PID control[C].Third International Conference on Genetic and Evolutionary Computing， Wgec 2009，Guilin， China，14－17 October.DBLP，2009:561－564.

[4] 韩坤，任春燕.基于滑模控制的线控转向系统仿真[J].湖北汽车工业学院学报，2013，27(3):1－4.

[5] 郑凯锋，陈思忠，王亚.基于线控技术的四轮转向全滑模控制[J].东南大学学报(自然科学版)，2013，43(2):334－339.

[6] WANG H，KONG H，MAN Z.Sliding mode control for steer-bywire systems with AC motors in road vehicles[J].IEEE Transactions on Industrial Electronics，2014，61(3):1596－1611.

[7] KAZEMI R，JANBAKHSH A A.Nonlinear adaptive sliding mode control for vehicle handling improvement via steer-by-wire[J].International Journal of Automotive Technology，2010，11(3):345－354.

[8] DO M T， MAN Z， ZHANG C， et al.Robust sliding mode-based learning control for steer-by-wire systems in modern vehicles[J].Vehicular Technology IEEE Transactions，2014，63(2):580－590.

[9] LIN F J， HUNG Y C， RUAN K C.An intelligent second-order sliding-mode control for an electric power steering system using a wavelet fuzzy neural network[J].IEEE Transactions on Fuzzy Systems，2014，22(6):1598－1611.

[10] REDDY C S R，KALAVATHI M S.Improved performance of a novel SMC-fuzzy controller for DTC brushless DC motor drive for precise speed regulation[C].IEEE Ninth International Conference on Power Electronics and Drive Systems.IEEE，2011:873－880.

[11] WANG J， RAD A B， CHAN P T.Indirect adaptive fuzzy sliding mode control:part I:fuzzy switching[J].Fuzzy Sets＆ Systems，2001，122(1):21－30.

[12] 黄卫华，方康玲，章政.典型模糊控制器的隶属函数设计及分析[J].模糊系统与数学，2010，24(5):83－90.