车辆自适应巡航控制系统的建模与分层控制∗
张亮修,吴光强,2,郭晓晓
(1.同济大学汽车学院,上海 201804; 2.东京大学生产技术研究所,东京 153-8505)
前言
作为巡航系统的增强升级技术,自适应巡航控制(adaptive cruise control,ACC)系统实时控制自车车速和自车与前车的车距,提升驾驶舒适性和安全性。近年来,ACC系统的研究呈现多元化,如城市工况起-停ACC[1]、混合动力车辆ACC[2]、ACC与车道保持相结合[3]、弯道行驶ACC[4]、考虑燃油经济性ACC[5]和综合协调跟踪性、燃油经济性和舒适性的多目标ACC[6]等。
对ACC系统研究须建立准确的车辆动力学模型,现有文献仅建立车辆纵向动力学模型,未考虑轮胎滑移和车辆纵/侧/垂向耦合特性的影响[7],且节气门和制动器难以准确反映执行器的实际物理特性[8]。ACC系统多采用分层控制结构,上层控制算法多从保持期望车距角度输出期望加速度,未考虑跟车过程中驾乘人员的舒适性[9],并且由于车辆自身非线性和外界干扰因素,下层控制算法的鲁棒跟随性和稳定性难以同时兼顾[10]。为此,本文中建立纵-侧-垂向耦合的14自由度整车模型、执行器模型和逆动力学模型,分别应用模型匹配控制理论和线性二次最优控制理论设计ACC系统分层控制器,最后仿真验证模型的准确性和控制算法的可行性。
1 底盘系统动力学建模
1.1 整车动力学建模
取整车质心在侧倾轴线的投影点为簧上质量坐标系o-xyz的原点,以汽车静止于水平路面时过原点的水平面与汽车纵向对称面交线为x轴,且向前为正,同一水平面内与x轴垂直的轴线定为y轴,向左为正,由右手定则确定z轴向上为正。建立纵-侧-垂向耦合的14自由度整车模型,整车纵向、侧向和横摆运动动力学方程分别为
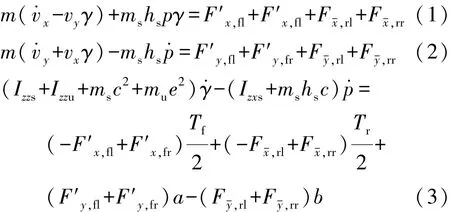
式中:m为整车质量;ms为簧上质量;mu为簧下质量;vx和vy分别为车辆纵向速度和侧向速度;p和γ分别为侧倾加速度和横摆角速度;hs为簧上质量质心与x轴的垂直距离;c和e分别为簧上质量质心和簧下质量质心相对整车质心距离在x轴方向的投影;Izzs,Izzu和Izxs分别为转动惯量;a和 b为整车质心到前、后轴的距离;Bf和 Br分别为前、后轮距;Fx-,ij和Fy-,ij分别为车轮的纵向轮胎力和侧向轮胎力(ij=fl,fr,rl,rr);F′x,fl,F′x,fr,F′y,fl和 F′y,fr表达式如下:
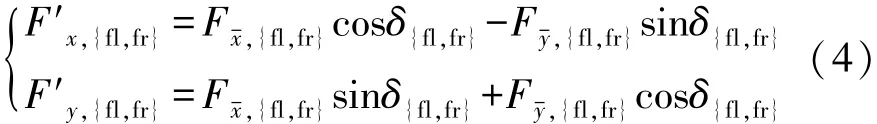
式中 δfl和 δfr为前轮转角。
簧上质量(车身)质心垂向、侧倾和俯仰运动动力学方程分别为
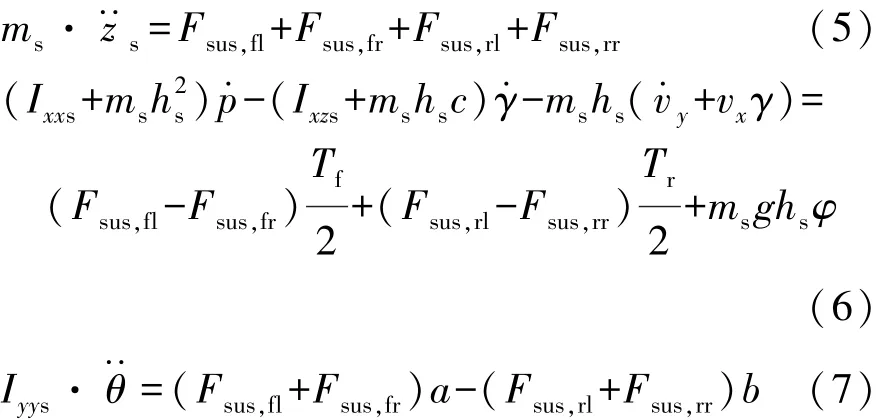
式中:为簧上质量质心垂向加速度;Ixxs,Ixzs和Iyys为转动惯量;φ和 θ分别为侧倾角和俯仰角;Fsus,{fl,fr,rl,rr}为 4 个车轮对应的悬架力。
4个车轮的转动和垂向运动方程分别为
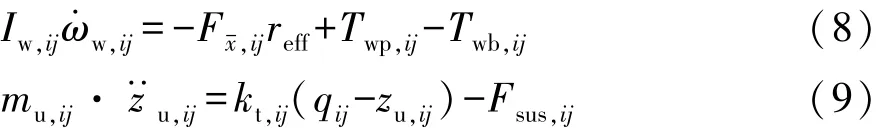
式中:Iw,ij为车轮转动惯量;ω·w,ij为车轮角加速度;reff为车轮有效半径;Twp,ij为作用于车轮的驱动力矩;Twb,ij为作用于车轮的制动力矩;z··u,ij和 zu,ij分别为车轮垂向加速度和垂向位移;kt,ij为轮胎垂向刚度;qij为路面垂向输入。
1.2 轮胎模型
利用魔术公式(magic formula,MF)轮胎模型来描述轮胎六分力与车轮运动参数之间的定量关系[11],其形式为
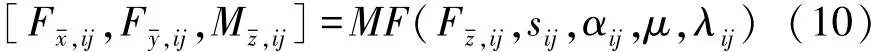
易知,轮胎力与车轮垂向载荷Fz-,ij、纵向滑动率sij、轮胎侧偏角αij、路面附着系数μ和车轮外倾角λij有关。
1.3 电子节气门模型
参照文献[12],建立电子节气门模型如下:

式中:状态变量[x1,x2]T=[αe,α·e]T,αe为节气门开度;控制量 u=Ea为电机输入电压;ksp,n,kt,Ith,km,kf,kb,Ra,ktf和 αe0为节气门物理结构参数。
1.4 液压制动器模型
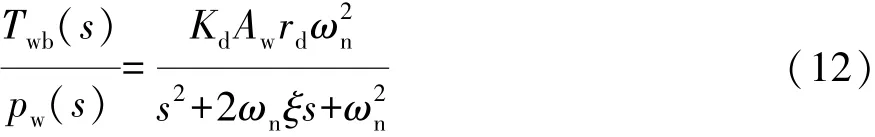
考虑制动器液压动态特性影响,制动力矩与轮缸制动压力的数学传递函数关系式为式中:Twb为制动力矩;pw为轮缸制动压力;Kd为制动效能因数;Aw为制动活塞横截面积;rd为制动盘有效半径;ωn为系统固有频率;ξ为阻尼系数。
2 车辆逆动力学建模
2.1 节气门/制动器切换逻辑
以实际车辆怠速带挡滑行的数据为基础,得到车辆加速度与车速的关系,以此作为驱动/制动切换基准,从舒适性角度,应避免驱动/制动控制的频繁切换,将基准偏置0.05m/s2,构成驱动控制下边界和制动控制上边界,如图1所示。
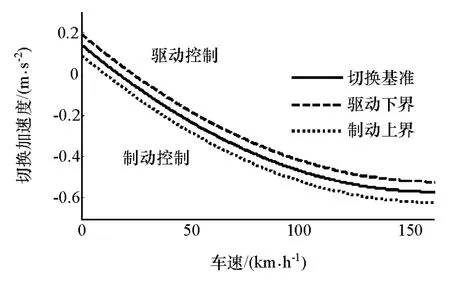
图1 节气门/制动器切换逻辑曲线
2.2 发动机逆模型
当切换为驱动工况时,首先根据期望加速度计算出期望的发动机转矩:
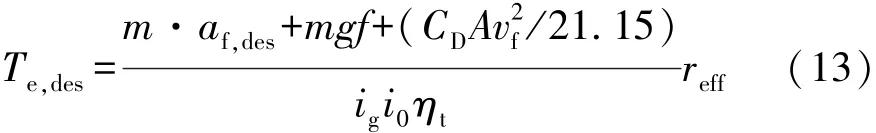
式中:Te,des为期望发动机转矩;af,des为期望加速度;f为滚动阻力系数;CD为空气阻力系数;A为迎风面积;g为重力加速度;ig和i0分别为变速器和主减速器传动比;ηt为传动系统机械效率。
然后由发动机逆模型三维MAP图通过查表得到期望的节气门开度,如图2所示。
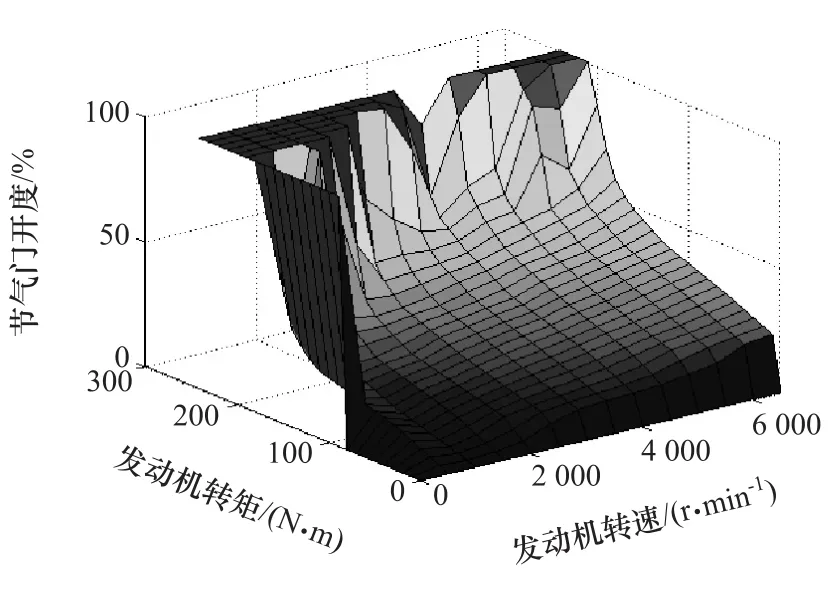
图2 发动机逆模型MAP图
2.3 制动器逆模型
当切换为制动工况时,在充分利用发动机制动、风阻和滚动阻力情况下,得到期望加速度所需要的制动力矩,由逆制动模型得到期望的制动压力:

式中:Twb,des为期望制动转矩;Kb为制动增益系数。
3 自适应巡航控制系统分层控制
本文中设计ACC系统分层控制器,如图3所示,上层控制器综合考虑车距、速度和加速度,通过线性二次最优控制理论得到期望的跟车加速度,下层控制器应用模型匹配控制理论,在考虑车辆自身参数时变、外界干扰和响应时滞等情况下,使车辆的实际加速度能快速、准确地跟踪期望加速度。
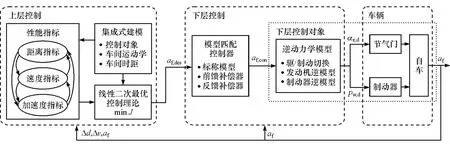
图3 自适应巡航控制系统分层控制架构
3.1 下层控制器设计
3.1.1 下层控制对象传递函数
由图3可见,下层控制对象的输入为控制加速度af,con,输出为实际加速度af。理论上,逆模型补偿后的下层控制对象的输入输出增益为1,由于包含驱动/制动切换、逆模型插值和挡位变换等各种非线性因素,采用单频激励法对系统传递函数进行辨识,以0.15~10rad/s为频率范围,不等间距选择20个激励频率,每个工作点处,又分整车质量为公称质量和120%公称质量。在不同的整车质量和激励频率下,依次仿真,记录系统的输入输出信号,如图4所示。
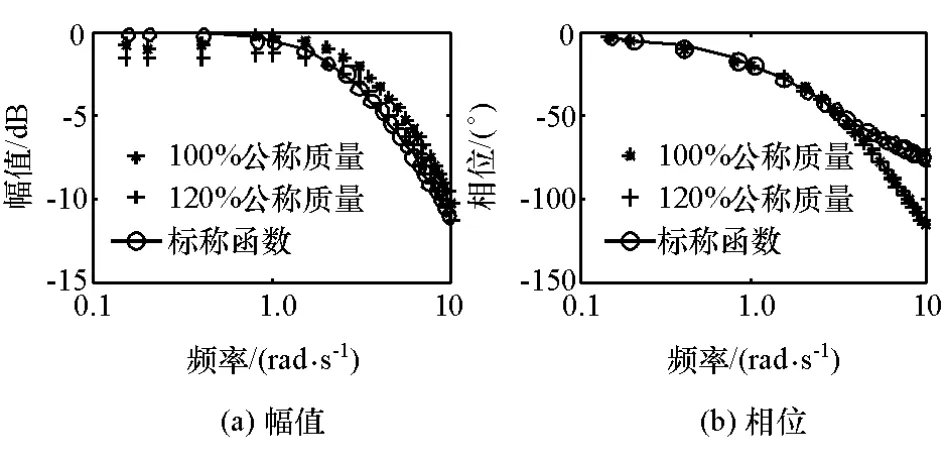
图4 下层控制对象辨识结果
取不同频响特性的平均值作为下层控制对象传递函数,称作标称函数,即

3.1.2 模型匹配下层控制器设计
模型匹配下层控制器结构如图5所示,由规范模型、前馈补偿器和反馈补偿器组成,前馈补偿器用于保证系统响应的快速性,反馈补偿器用于保证系统的鲁棒稳定性。图中:ar为以规范模型传递特性实现的期望加速度,称为参考加速度;e为控制误差量;wd为外界干扰量。
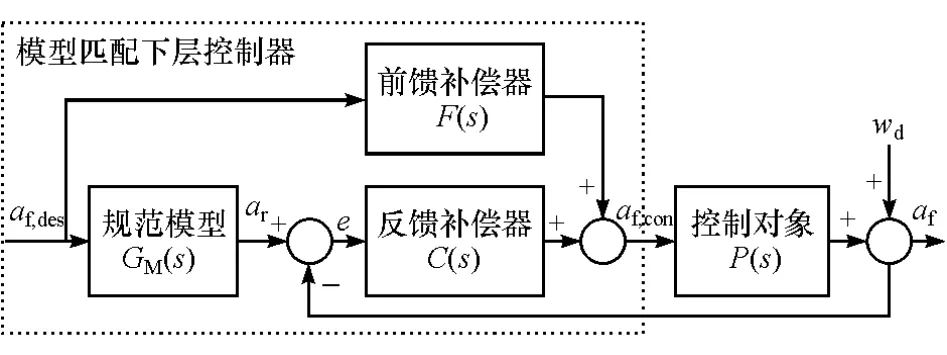
图5 模型匹配下层控制器结构
模型匹配下层控制器的设计目的是在全面考虑外界干扰和控制对象传递特性在一定范围内变动的情况下,使系统的传递特性与规范模型的传递特性相同[13]。规范模型的设计主要考虑系统响应规范性的要求,取系统的规范模型为

理想情况下,系统不受外界干扰,标称传递函数P(s)能够准确描述下层控制对象的传递特性,此时从输入af,des到输出af的传递函数为
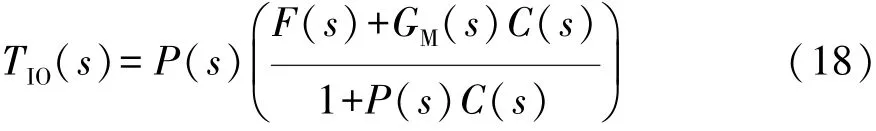
令前馈补偿器F(s)为

则TIO(s)=GM(s),理想情况下系统的规范输入输出特性只须通过前馈补偿器即可实现。
考虑下层控制系统存在外部扰动及模型误差的情况,则实际下层控制对象传递函数为

式中Δm表示模型的乘法误差。
此时,从输入af,des到输出af的传递函数为
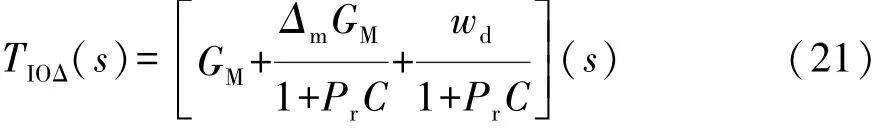
式(21)中后两项分别是由于模型误差和外界干扰带来的系统控制误差,须利用反馈补偿器来减小或消除这两项误差,保证控制系统的稳定性和鲁棒性。利用 H∞控制理论设计鲁棒反馈补偿器C(s),其设计目标是使下层反馈闭环系统稳定,并使下式成立:

式中:S(s)为wd=0时从输入ar到控制误差量e的传递函数,定义为反馈控制系统的灵敏度函数;T(s)为Δm=0,wd=0时从输入ar到输出af的传递函数,定义为系统的补灵敏度函数;R(s)为从干扰量到控制量的传递函数,定义为控制灵敏度函数;We(s),Wy(s)和Wu(s)分别是相应的加权函数。
Wy(s)用于在下层控制对象存在模型误差时保证系统的鲁棒性,根据模型误差上界,获得反馈控制系统补灵敏度加权函数为

We(s)用于保证下层控制系统具有良好的低频跟踪性能,即要求控制系统无静态误差,选择系统灵敏度加权函数形式为

式中a和b为待定参数,其值依据控制系统性能要求和控制问题可解条件确定。
Wu(s)用于防止高频扰动对控制量的影响,防止出现过大的高频控制量,选取

按照标准H∞控制问题的状态空间解法,求得鲁棒反馈补偿器的传递函数表达式为
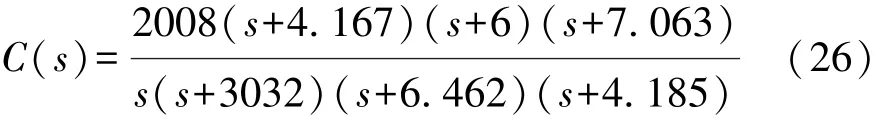
3.2 上层控制器设计
图6示出了自车与前车的纵向运动学关系,定义:

式中:Δd为车间距误差;Δv为前车和自车相对速度;d和ddes分别为实际车间距和期望车间距;vp和分别为前车和自车速度。
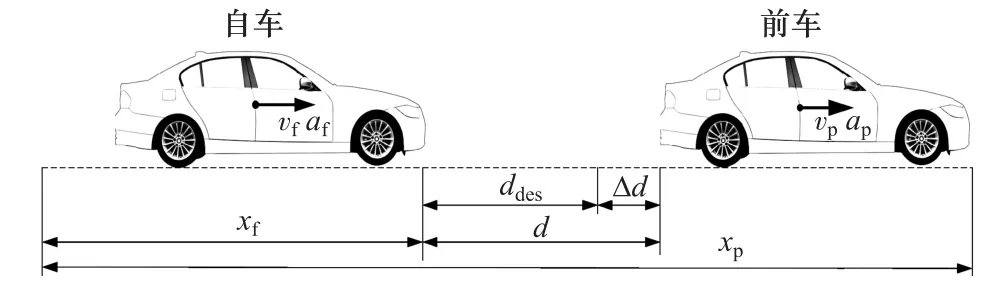
图6 ACC纵向运动学示意图

期望车间距采用固定车间时距,即式中:τh为车间时距;d0为自车停止后与前车最小安全车距。
自车实际加速度af和期望加速度afdes关系可用1阶惯性环节表示:

式中:KL为系统增益;TL为时间常数。
以 Δd,Δv 和 af为状态变量,以 af,des为控制输入,视ap为系统扰动,得到如下状态方程:

其中
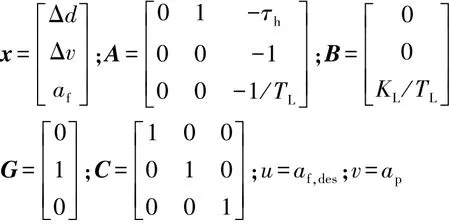
对于跟车系统,控制目标是使自车与前车的实际车距趋近于期望车距,自车车速趋近于前车车速,即要求车距误差Δd和相对车速Δv趋近于零。
文献[14]中通过大量试验数据分析指出,自车加速度越小,乘坐舒适性越高,为此,通过优化加速度绝对值,提高跟车舒适性,即min(|af|)。
因此,建立综合考虑车距、相对速度和自车加速度的多目标优化指标:
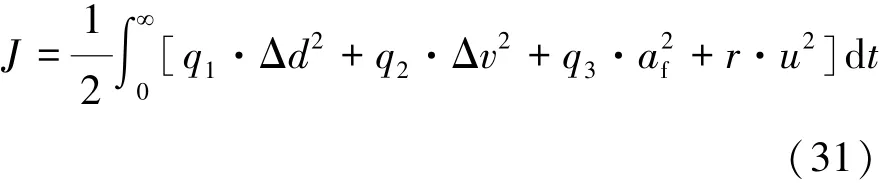
式中:q1,q2和q3分别为车距误差、相对速度和自车加速度的加权系数;r为控制输入加权系数,用于限制控制量的抖动。
基于线性二次最优控制理论,寻求优化指标J最小的期望跟车加速度。
4 仿真分析
在Matlab/Simulink环境下搭建ACC系统模型和分层控制算法,仿真参数见表1。

表1 仿真参数
设定前车初速度为15m/s,在0~10s保持匀速运动,10~20s以1m/s2的加速度做匀加速运动,20~30s保持匀速运动,30~40s以-0.5m/s2的减速度做匀减速运动,40~50s再次保持匀速运动,50~70s做变减速运动,前车初始位移为40m;假设自车初速度10m/s,初始位移为0。仿真结果如图7所示。
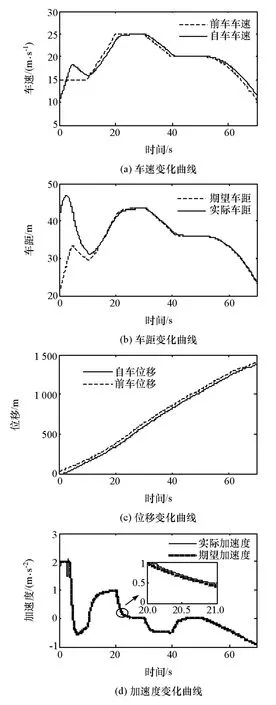
图7 自适应巡航控制仿真结果
由图7(a)可见,前车0~10s匀速行驶时,因自车初速小于前车初速,故在ACC系统作用下,自车逐渐加速而迅速接近前车,在6s左右超调后又迅速收敛于前车车速,在10~20s前车匀加速运动时,自车始终保持跟车状态,在20~30s和40~50s前车做匀速运动时,自车以相同车速保持匀速运动,而在30~40s和50~70s前车分别匀减速和变减速行驶时,自车能及时减速,避免与前车发生碰撞,考虑到前车信息获取的延时性等因素,自车车速有一定滞后,但在实际合理范围内。由图7(b)可知,实际车间距能精确地跟踪期望车间距,且在前车减速时略大于期望车间距,保证车辆行驶安全性。由图7(c)可知,自车位移始终与前车位移保持一致,并保证前车急减速时有足够的安全距离。由图7(d)可知,自车实际加速度能精确、快速地跟踪期望加速度。
图8为执行器控制仿真结果。由图可见,实际节气门开度和制动压力能准确地跟踪期望节气门开度和制动压力。

图8 执行器控制仿真结果
5 结论
(1)所建立的14自由度整车模型和逆动力学模型能满足车辆自适应巡航控制对系统模型的要求。
(2)模型匹配下层控制器使控制系统有效抵抗车辆动力学系统的非线性与车辆质量变动和道路坡度与风阻等外部干扰因素,并保证较快的跟踪速度和较小的静态误差。
(3)上层控制器通过线性二次最优控制理论得到综合考虑车距、相对速度和自车加速度的期望跟车加速度,符合实际跟车加速度需求。
(4)仿真结果表明,ACC系统能控制车辆在加速行驶、稳态跟车和制动减速等工况下均能保持良好的跟踪性和适应性。
[1] SHAKOURI P,ORDYSA,ASKARIM R.Adaptive cruise control with stop&go function using the state-dependent nonlinear model predictive control approach[J].ISA Transactions,2012,51(5):622-631.
[2] GANJIB,KOUZANI A Z,KHOOSY,et al.Adaptive cruise control of a HEV using sliding mode control[J].Expert Systems with Applications,2014,41(2):607-615.
[3] DANG R, WANG J, LI S E, et al.Coordinated adaptive cruise control system with lane-change assistance[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(5):1-11.
[4] 张德兆.基于弯道行驶的车辆自适应巡航控制[D].北京:清华大学,2011.
[5] LI SE,HU X,LI K,et al.Mechanism of vehicular periodic operation for optimal fuel economy in free-driving scenarios[J].Intelligent Transport Systems Iet,2015,9(3):306-313.
[6] LI S,LIK,RAJAMANIR,et al.Model predictive multi-objective vehicular adaptive cruise control[J].IEEE Transactions on Control Systems Technology,2011,19(3):556-566.
[7] FANCHER P,PENG H,BAREKET Z,et al.Evaluating the influences of adaptive cruise control systems on the longitudinal dynamics of strings of highway vehicles[J].Vehicle System Dynamics,2016,37(1):125-136.
[8] 裴晓飞,刘昭度,马国成,等.基于节气门与制动联合控制的自适应巡航控制系统[J].汽车工程,2013,35(4):375-380.
[9] 李朋,魏民祥,侯晓利.自适应巡航控制系统的建模与联合仿真[J].汽车工程,2012,34(7):622-626.
[10] ALIZ,POPOV A A,CHARLESG.Model predictive control with constraints for a nonlinear adaptive cruise control vehicle model in transition manoeuvres[J].Vehicle System Dynamics,2013,51(6):943-963.
[11] PACEJKA H B.Tyre and vehicle dynamics[M].Butterworth-Heinemann,2002,ISBN 0 7506 5141 5.
[12] 陈虹,胡云峰,郭宏志,等.基于backstepping方法的电子节气门控制[J].控制理论与应用,2011,28(4):491-496.
[13] 侯德藻,高锋,李克强,等.基于模型匹配方法的汽车主动避撞下位控制系统[J].汽车工程,2003,25(4):399-402.
[14] MOON S,YI K.Human driving data-based design of a vehicle adaptive cruise control algorithm[J].Vehicle System Dynamics,2008,46(8):661-690.

