非圆齿轮齿廓曲线设计的力臂函数法
程 金 石, 孔 祥 沅
( 大连工业大学 机械工程与自动化学院, 辽宁 大连 116034 )
0 引 言
非圆齿轮是对滚节曲线不再为圆或圆弧形,而是按给定传动比变化规律设计的一种实现非线性传动的异形齿轮[1]。它主要在仪器仪表[2-3]和自动装置[4]中实现特殊的运动和函数运算[5],如摆动[6]、分度[7]、变速[8]等。一对非圆齿轮节曲线的纯滚动是靠主动轮齿廓推动与之共轭的从动轮齿廓进行的,并且非圆齿轮每个齿的齿廓都不同,因此,针对不同的应用场合如何准确高效地找到更合适的共轭齿廓及其设计方法尤为重要。非圆齿轮齿廓求解方法主要有解析法、折算齿形法[1]、齿廓的渐屈线法[9]、包络加工法和齿廓法线法[10]等。其中求解非圆齿轮共轭齿廓常用的已知条件为加工刀具和共轭齿廓,如可利用齿轮刀[11]或非圆齿轮主动轮做刀具[12],并结合凸包算法中的Jarvis步进法来优化刀具包络生成非圆齿轮齿廓的方法[13]。此外,文献[14-15]提出定啮合角原理求解非圆齿轮共轭齿廓。Lozzi[16]通过推导椭圆齿轮渐开线齿廓的4种可能的基曲线类型求解椭圆齿轮共轭齿廓。而设计非圆齿轮共轭齿廓方法是设定和表达已知条件的方法。文献[17-18]基于Roulette理论,通过建立瞬心线、旋轮线和接触迹之间的数学模型来设计非圆齿轮共轭齿廓。林菁[19]提出构造啮合角函数直接设计非圆齿轮齿廓的啮合角函数法。文献[20-21]通过建立任意形式的齿条刀齿廓或啮合轨迹模型,设计自由形式非圆齿轮共轭齿廓。
上述方法均以几何条件作为初始设计条件,传动特性被动得到。本研究基于齿廓主动设计理念,提出一种直接将传动特性作为设计条件,通过构造传动特性函数并几何化,进而求得齿廓曲线。这样得到的非圆齿轮齿廓曲线既满足Willis定理,又能实现预期的传动特性。
1 齿廓曲线的设计条件
一对非圆齿轮的传动过程可以看作是两条节曲线相切地做纯滚动。此间,至少有一对共轭齿廓处于啮合状态。节曲线上不同点成为瞬心时,齿廓曲线上有相应的点成为啮合点。因此,齿廓曲线可以看作是节曲线的伴随曲线。根据Willis定理,齿廓曲线可以表示为

(1)
式中:θ为瞬心线上点的相位角,作为运动瞬时参数;r(θ)和R(θ)分别为瞬心线上和齿廓曲线上对应θ瞬时的点;n(θ)为R(θ)的法矢,始终指向R(θ) 外侧;l(θ)为沿n(θ)方向r(θ)到R(θ)的位移。
由式(1)中R(θ)得
R′(θ)=r′(θ)+l′(θ)·n(θ)+l(θ)·n′(θ)
(2)
式(2)代入式(1)R′(θ)得

(3)
式中:θc为齿廓曲线与节曲线相交时对应的运动瞬时参数。可见,l(θ)不是独立的参数。在给定节曲线r(θ)条件下,齿廓曲线R(θ)完全决定于n(θ),齿廓曲线的设计条件就是设计n(θ)函数。当按与r′(θ)的夹角为常数设计n(θ)时,即为齿条法;当按与r(θ)垂线的夹角α设计n(θ)时,即为啮合角函数法。本文通过反映传动特性的力臂函数设计n(θ)求解齿廓曲线。
2 力臂函数
如图1所示,当非圆齿轮节曲线上r(θ)为瞬心时,齿廓上R(θ)为啮合点。若忽略摩擦,该啮合点所受接触力F必沿内法线方向,即沿n(θ)的反方向。过回转中心O作n(θ)的垂线,垂足为B,设O到B的距离为b。可以看出,b就是接触力驱动齿轮绕O点回转的力臂。显然,b是θ的函数,即b=b(θ)。对于具体机构,由机构负载条件可以得出驱动力矩函数M(θ)。而M(θ)=F(θ)·b(θ),所以可以通过调整b(θ)的大小来控制F(θ),以满足一定受力准则。相反,在已知M(θ) 条件下,为获得按受力准则确定的F(θ),b(θ) 必须满足一定条件,即b(θ)=M(θ)/F(θ),由此得到b(θ)函数称为力臂函数。由力臂函数确定的B点的轨迹称为力臂曲线,记为B(θ),见图1。设B(θ)到r(θ)的转角为α,则有
(4)
式中:|r(θ)|是r(θ)的模。故B(θ)的方程为
B(θ)=b(θ)·e(θ+α)
(5)
式中:e(θ+α)为圆矢量函数。
对于给定的非圆齿轮机构,运动规律决定了节曲线形状,负载规律和受力条件决定了力臂曲线形状。所以,节曲线可以看作是机构运动信息的几何表征,力臂曲线可以看作是机构驱动信息的几何表征。通过这两条曲线设计的齿廓,既可以满足运动条件,又可以满足驱动条件。
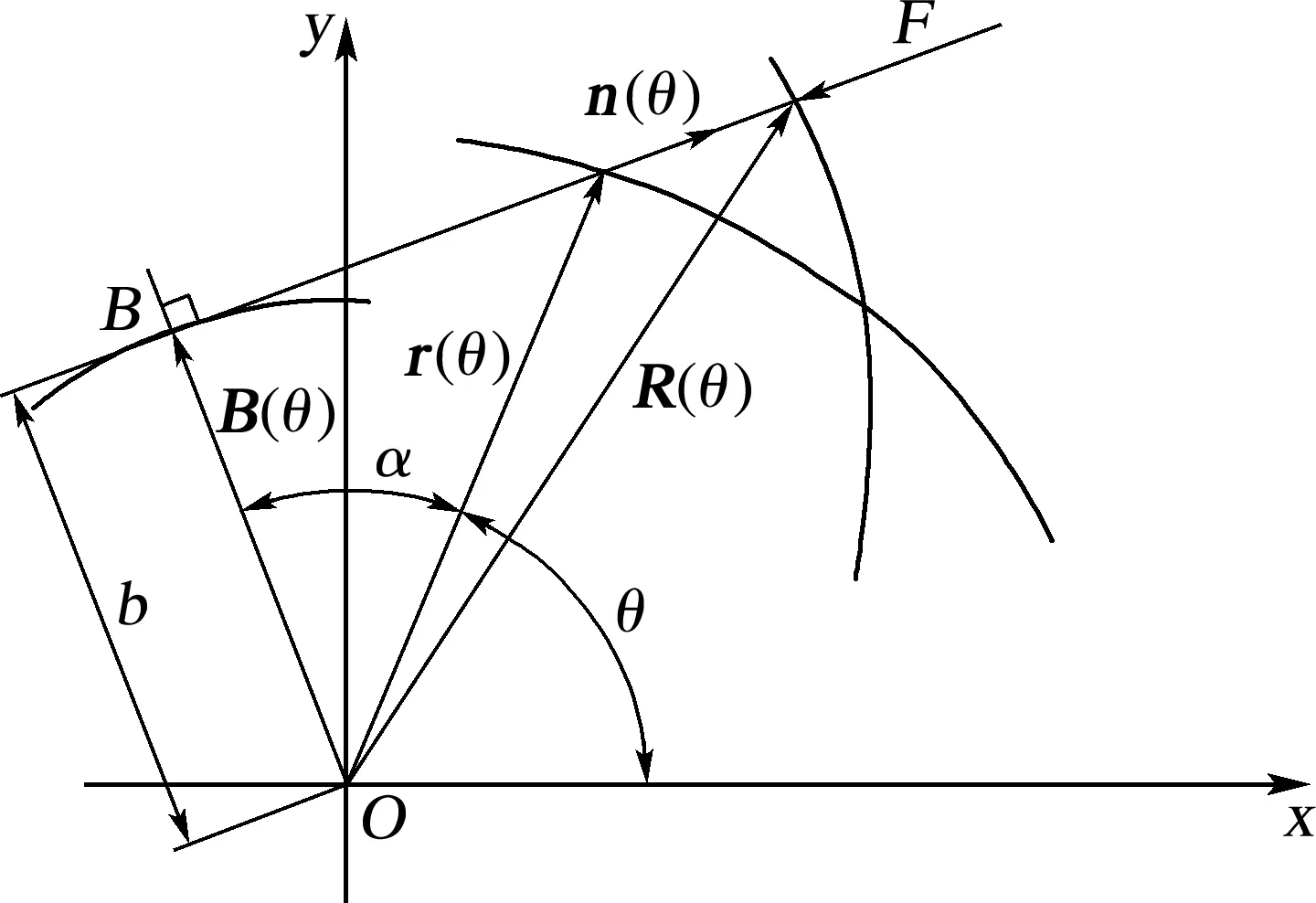
图1 力臂曲线与齿廓法矢
此外,图1中的α角和文献[19]中啮合角在数值上完全相等,这给本文设计齿廓的几何分析带来便利。
3 力臂函数法的原理
齿廓曲线的设计在本质上就是设计齿廓曲线的外法矢n(θ)。该法矢既要过瞬心r(θ),又要过力臂端点B(θ),以实现要求的力臂b(θ)。其方向应与啮合点受力方向相反,即由B(θ)指向r(θ)。所以齿廓外法矢n(θ)为
(6)
式中,B(θ)≠r(θ)。对于非圆齿轮来说,齿廓曲线有左右两侧之分,啮合时分别驱动齿轮逆时针回转(正齿廓)和顺时针回转(负齿廓)。针对具体齿轮的不同回转方向,力臂函数可根据负载条件和力学准则设计为相同函数或不同函数。力臂函数确定之后,对于正齿廓曲线,力臂曲线方程B(θ)可由公式(5)得出;而对于负齿廓曲线,力臂曲线方程则变为
B(θ)=b(θ)·e(θ-α)
(7)
在已知节曲线条件下,运用力臂函数及力臂曲线,确定齿廓曲线法矢n(θ),进而得到齿廓曲线的方法称为齿廓曲线设计的力臂函数法。
力臂函数法设计齿廓曲线的优点在于所有同侧齿廓的设计基于一个力臂函数,而这个力臂函数的得出是基于一定的接触力条件和接触强度准则等传动特性。故所得齿廓可使非圆齿轮副传动时能实现预期的传动特性,达到提高接触强度、降低振动和噪音等目的。而基于单个齿廓的设计方法,由于节曲线的非圆特性及齿廓的离散特性,不同齿廓的力臂曲线可能不同。这将导致不同齿廓啮合时驱动力臂跳跃式变化,进而导致接触力突变,由此带来振动冲击、噪音等不利影响。
4 齿廓曲线的等距特性
在公式(3)中,当θ=θc时,l(θ)=0,此时R(θ)=r(θ),即齿廓曲线上的点R(θc)与节曲线上的对应点r(θc)重合。在给定节曲线和力臂曲线条件下,θc取不同值时,由公式(3)及公式(1)将得到不同的齿廓曲线,这些齿廓曲线分别与节曲线交于不同的r(θc)点,这些交点称为节曲线的分齿点。可见,过节曲线上不同的分齿点可以得到不同的齿廓曲线,可以用分齿点的位置参数θc表征齿廓曲线。
设同一对节曲线和力臂曲线条件下,有两条齿廓曲线R1(θ)和R2(θ),见图2。由于在同一坐标系下,不同齿廓曲线对应同一θ的r(θ)和n(θ) 均相同,所以这两条齿廓曲线的方程为
(8)
(9)
由式(8)、式(9)得
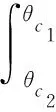


(10)
令

(11)
则对于给定的两条齿廓曲线l21为常数。于是有
R2(θ)=r(θ)+l2(θ)·n(θ)=
r(θ)+[l21+l1(θ)]·n(θ)=
R1(θ)+l21·n(θ)
(12)
由于n(θ)为R1(θ)的法矢且l21为常数,所以公式(12)表明,R2(θ)为R1(θ)的等距曲线。考虑到θc1和θc2的一般性,可以得出结论:在给定节曲线和力臂曲线条件下,过节曲线上不同分齿点的齿廓曲线均为等距曲线。此结论的重要意义在于:利用一条整周期的齿廓曲线即可描述所有同侧齿廓的几何信息,这给非圆齿轮的齿廓设计和分析带来极大便利,也是本文所述齿廓设计方法的另一个优点。
整周期齿廓曲线的起点应位于力臂曲线,假设此时对应的参数为θ0。对于正齿廓曲线,转角以逆时针为正,θ0小于θc且满足

(13)
此时,由公式(1)、(3)、(6)有:R(θ0)=B(θ0)。整周期齿廓曲线终点对应的参数为
θ1=θ0+2π
(14)
对于负齿廓曲线,转角以顺时针为正,公式(13)及(14)仍然成立。
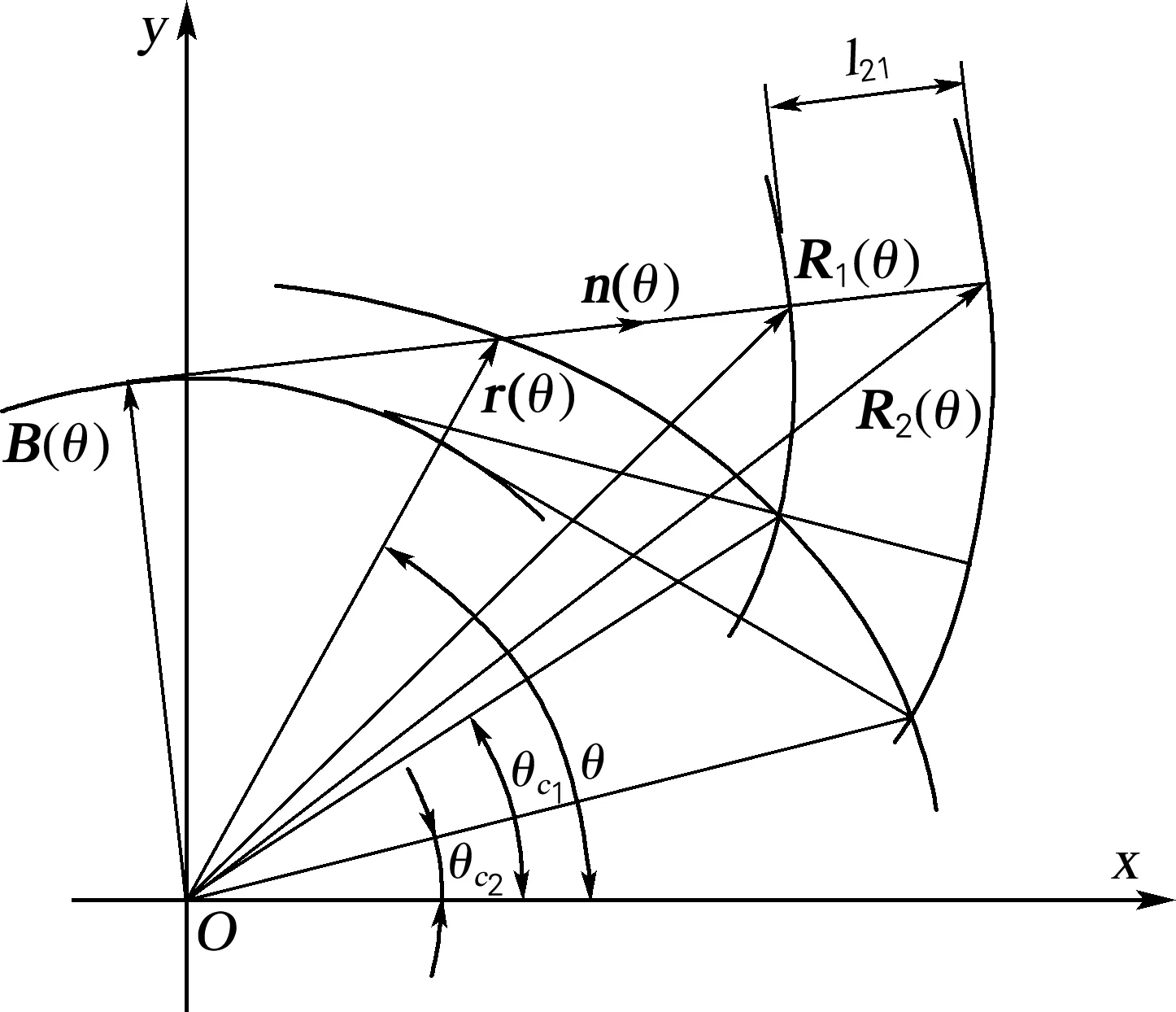
图2 齿廓曲线的等距性
5 设计步骤及实例
5.1 设计步骤
基于力臂函数法原理及齿廓曲线的等距特性,非圆齿轮齿廓设计步骤如下:
(1)由机构运动规律求出节曲线r(θ);
(2)确定节曲线上各分齿点位置θci;
(3)由负载条件和受力准则求出力臂函数b(θ) 及力臂曲线B(θ);
(4)由式(6)确定齿廓法矢n(θ);
(5)由式(3)及式(1)求出过分齿点θc1的整周期齿廓曲线R1(θ);
(6)利用等距特性由公式(11)、(12)求出过其他分齿点的齿廓曲线R2(θ);
(7)以齿顶曲线和齿根曲线截取各齿廓曲线,并作出过渡曲线。
至此,非圆齿轮的一侧齿廓设计完成,另一侧齿廓设计亦按同样步骤。与之啮合的另一个非圆齿轮的齿廓则可按齿廓法线法直接求得,无须单独设计。
5.2 计算实例
以椭圆节曲线齿轮为例,取其几何中心为齿轮回转中心,椭圆参数:半长轴a=28,偏心率e=0.6。力臂曲线为圆心与椭圆中心重合的圆,圆半径为20,即力臂函数b(θ)=20。利用Matlab编程得到的完整齿廓曲线,如图3所示。图中V1为正转齿廓曲线,V2为反转齿廓曲线。

图3 正转及反转完整齿廓曲线
设齿轮齿数z=17,按等极角方式分齿(即各相邻分齿点弧段对齿轮中心的张角相等),齿顶高为1.4,齿根高为1.5,得到的各齿廓曲线如图4所示。图中所有正转齿廓均为图3中V1的等距曲线,可在该曲线上截取并作等距线得到。同样,所有反转齿廓均可由图3中V2上截取并作等距线得到。

图4 同侧齿廓曲线的等距性
需要说明的是,本算例只是表明利用力臂函数法生成齿廓曲线的可行性,具体参数的合理性及优化求解有待后续研究。
6 结 论
在给定运动规律(或节曲线)条件下,齿廓曲线完全决定于其法矢n(θ),设计齿廓曲线就是设计其法矢n(θ)。反映负载条件和受力准则的力臂函数可以作为齿廓曲线法矢设计的有效工具,它建立了齿廓几何特征和运动副传动特性的联系。选取合适的力臂函数后,基于本文方法得到的同侧齿廓互为等距曲线,一条整周期的齿廓曲线可反映所有同侧齿廓的几何信息,给非圆齿轮的齿廓设计和分析带来很大便利。
按力臂函数法所设计的非圆齿轮齿廓不是以齿条齿廓为必要几何条件,故齿条类刀具的滚齿或插齿不是其通用加工方法。对于直齿非圆齿轮,线切割是其有效加工手段。若需进一步精加工,可在工作台具有两个移动坐标和一个回转坐标的数控机床上采用蝶形砂轮端面磨削完成。而对于斜齿非圆齿轮的加工则需进行后续研究和探讨。
[1] 李福生.非圆齿轮[M].北京:机械工业出版,1975.
[2] 丁凡,邓民胜,刘硕,等.耐高压双向椭圆齿轮微小流量计研究[J].农业机械学报,2015,46(6):327-333.
[3] 刘大伟,任廷志,金昕.空间非圆齿轮双侧同步驱动板坯结晶器非正弦振动的研究[J].中国机械工程,2015,26(17):2325-2329.
[4] BENDEFY A G, PIROS A, HORK P. Arbitrary vehicle steering characteristics with changing ratio rack and pinion transmission[J]. Advances in Mechanical Engineering, 2015, 7(12): 1-12.
[5] LITVIN F L, GONZALEZ P I , FUENTES A, et al. Design and investigation of gear drives with non-circular gears applied for speed variation and generation of functions[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(45/46/47/48): 3783-3802.
[6] TERADA H, ZHU Y, SUZUKI M, et al. Development of a knee motion assist mechanism for wearable robot with a non-circular gear and grooved cams[C]//Mechanisms, Transmissions and Applications. Dordrecht: Springer, 2012: 69-76.
[7] ZHENG F Y, HUA L, HAN X H, et al. Synthesis of indexing mechanisms with non-circular gears[J]. Mechanism and Machine Theory, 2016, 105: 108-128.
[8] 贾巨民,高波,索文莉,等.越野汽车新型变速比差速器的研究[J].中国机械工程,2012(23):2844-2847.
[9] WU L I, CHANG S L. The base curves and tooth profiles of involute elliptical gears[J]. Journal of the Chinese Society of Mechanical Engineers, 1995, 16(2): 133-140.
[10] 童婷,郑方炎,孙科,等.基于齿廓法线的非圆齿轮齿廓数值算法[J].武汉理工大学学报(交通科学与工程版),2013(3):652-654.
[11] 史勇,王生泽.非圆齿轮齿廓数值算法研究[J].机械科学与技术,2013,32(8):1130-1133.
[12] 俞高红,虞佳萍,童俊华,等.一种共轭凹凸型非圆齿机构的设计[J].中国机械工程,2016,27(16):2155-2165.
[13] LI B T, HU J Q, CHEN D F, et al. Numerical algorithm of noncircular gear’s tooth profile based on jarvis march[C]//HCC 2016 Revised Selected Papers of the Second International Conference on Human Centered Computing. Colombo: Springer, 2016: 689-694.
[14] 曹利新,吴宏基,刘健.变速比定啮合角齿轮副啮合原理[J].大连理工大学学报,2000,40(1):89-93.
[15] DANIELI G A, MUNDO D. New developments in variable radius gears using constant pressure angle teeth[J]. Machanism and Machine Theory, 2005, 40(2): 203-217.
[16] LOZZI A. Non-circular gears-graphic generation of involutes and base outlines[J]. Journal of Mechanical Engineering Science, 2000, 214(3): 411-422.
[17] HORIUCHI Y. On the gear theory suggested by Leibnits[J]. Bulletin of the Japan Society of Precision Engineer, 1989, 23(2): 146-151.
[18] 崔希烈.非圆齿轮齿廓分析(一)[J].机械传动,1985,9(6):18-21.
[19] 林菁.共轭曲线啮合角函数理论及其应用[M].北京:科学出版社,2005.
[20] DONG H M, TING K L, YU B W, et al. Differential contact path and conjugate properties of planar gearing transmission[J]. Journal of Mechanical Design, 2012, 134(6): 061010.
[21] YU B W, TING K L. Free-form conjugation modeling and gear tooth profile design[J]. Journal of Mechanisms and Robotics, 2013, 5(1): 011001.

