微波热解炭化炉谐振腔的设计与仿真
徐 浩, 祝 守 新, 王 学 俊, 赵 维 维,彭 黄 湖, 杨 帆, 车 磊, 张 旭
( 1.大连工业大学 机械工程与自动化学院, 辽宁 大连 116034;2.湖州师范学院 工学院, 浙江 湖州 313000;3.浙江宜可欧环保科技有限公司, 浙江 湖州 313000 )
0 引 言
传统处理有机质固废的方式有堆放、排放、焚烧和掩埋,这些方式均存在环境污染、生物质能利用水平低等问题[1-3]。对有机质固废进行热解处理制备得到合成气、生物油等替代燃料是目前的一个研究热点。微波热解与传统处理方式相比,具有节能、环保、高效、可控等优势[4-5]。微波热解作为一种新的处理方式得到越来越多的关注和研究。目前,微波热解主要应用在麦秸秆[6]、玉米秸秆[7]、废弃茶叶[8]、松木块[9]及油棕榈树[10]等生物质废物方面。因为有机质固废热解炭化过程需保持在600 ℃以上[11],单个磁控管加热能力有限,一般需要采用多个磁控管协同工作。对于多磁控管加热情况,若馈口数目和馈口位置设计不合理,将使谐振腔内场分布不均匀,导致微波热解炭化炉工作效率低下,因此限制了微波热解在工业有机质固废热解处理中的应用。如何提高大型微波热解炭化炉的工作效率,特别是改善谐振腔中场的均匀性,是一个亟待解决的问题。
张伟燕等[12]对多模谐振腔进行了仿真设计,采用在谐振腔同一侧面分别布置单馈口、两馈口、三馈口的方式进行对比实验,分析了馈口数量的变化对谐振腔内场分布的影响,认为馈口数量的增加会增加腔体内电磁场。Bressan等[13]研究了两馈口对称分布时谐振腔内场的分布情况,并进一步分析比较了两馈口在两侧面不同位置时谐振腔内场的分布情况,认为馈口对称分布与非对称分布时,腔体内场强有很大差异。张景强等[14]对尺寸为260 mm×280 mm×180 mm的谐振腔进行设计,仿真分析馈口数目、大小、位置不同时微波电磁场的分布情况,发现馈口分布宜采用三馈口中心对称布置方式,且设置馈口大小为70 mm×50 mm×20 mm,这样腔体内电磁场分布效果最佳。现有的研究表明,馈口数目、位置、布置方式对谐振腔内场的分布均会产生影响。但是,对于多个磁控管协同加热的情形研究还比较少,还没有得出一种适合多馈口分布的最佳方案。
本研究基于微波技术波导理论和矢量分析法,借助软件HFSS对微波热解炉进行实体建模,模拟分析不同数目、不同布置形式的馈口分布下谐振腔内场的分布。其中,馈口分布方案包括单馈口、两馈口和四馈口,在两馈口和四馈口中,分别研究E-E型、H-H型和E-H型3种对称分布。通过多种方案的比较,验证分析馈口数目,尤其是馈口位置对谐振腔内场的分布的影响,得出四馈口激励的最佳分布方案。
1 谐振腔模型选择
常用的微波谐振腔分为单模谐振腔与多模谐振腔。单模谐振腔的优点是品质因数高、储能大[15];缺点是体积小、腔内场强分布不均匀,不适合分散加热物料。多模谐振腔内很多电场模式并存,各模式的电场相互叠加,在腔体内形成比单模谐振腔更加均匀的电磁能分布,实现物料的均匀加热,因此微波加热领域内常使用多模谐振腔。
本实验的仿真对象采用多模矩形谐振腔,模型如图1所示。其中,谐振腔的尺寸为400 mm×380 mm×320 mm;内部放置待加热处理的有机质废弃物,尺寸为300 mm×300 mm×50 mm。建模时假设谐振腔的横截面形状和媒质特性沿z轴不变化,即具有轴向均匀性,避免横截面形状和媒质对腔体内部场强产生影响。

图1 谐振腔仿真模型
2 馈口布置方案设计理论
2.1 微波技术波导理论
标准矩形波导的基本宽度和基本高度比为1∶2,即波导口的横截面有短边和长边之分,则馈口在腔体侧面布置时有两种基本形式,如图2所示。将长边与水平面平行的分布形式定义为E型,将短边与水平面平行的分布形式定义为H型。则E-E型为两个E型分布的馈口对称分布,H-H型为两个H型分布的馈口对称分布,E-H型为一个E型分布的馈口与一个H型分布的馈口对称分布。

图2 馈口的两种分布形式
微波作为一种电磁波,在传输过程中,电场和磁场同时存在,且位于相互垂直的两个平面内,如图3所示。

图3 沿z轴传播的电磁波传播示意图
对于图1所示的矩形微波谐振腔,根据微波技术波导理论可知,在谐振腔中能建立TE模和TM模两个系列的电磁场[16]。
研究多馈口分布位置和布置形式的不同对腔内场分布的影响,即电场和磁场、不同模式的波之间的相互干涉。单馈口采用不同角度放置时,谐振腔内电压驻波比与物料表面电场分布情况都不同,而当馈口采用E型分布和H型分布时,腔体内电压驻波比最接近1,即发射系数最小,不同模式的波之间的干扰最小[17]。因此,E型分布和H型分布有着重要的研究价值,本实验以这两种分布作为研究基础。
2.2 矢量运算规则
矢量运算如图4所示。在图4(a)中,E和H同一方向,两者之间相互叠加,得到C=E+H,结果为|C|=||E|-|H||,在数值上将小于两者原来的数值大小;图4(b)中,E和H之间有一角度α,且0<α<90°,结果为|C|=||E|cosα-|H||,E和H之间依然存在抵消;图4(c)中,E和H相互垂直,两者之间互不影响。
对于图5所示的两列相向传播的电磁波,在馈口E-E型分布与H-H型分布中,对称分布的磁控管通过馈口输出的电场和磁场分别处于同一平面,电场和磁场会分别进行叠加,相互抵消,损耗较大。而E-H型分布中,对称分布的磁控管通过馈口输出的电场和磁场所在的平面互相垂直,干涉最小,使得磁控管输出的能量最大化,效率最高。由图4矢量运算示意图可推测,E-H型分布应该是多馈口分布的一种最优分布方案。

图4 矢量运算示意图

图5 电磁波相向传播示意图
3 馈口布置方案选择
在文献[7-8]的研究基础上,首先对单馈口和两馈口腔内场的分布进行研究,然后考虑有机质固废微波热解炭化对高温均匀加热的要求,讨论四馈口腔内场的分布。为方便研究,将谐振腔的左右侧面记为A面和B面。对于单馈口和两馈口,设计5个方案:(1)单馈口分布在B面;(2)两馈口分布在B面;(3)两馈口E-E型对称分布在A面和B面;(4)两馈口H-H型对称分布在A面和B面;(5)两馈口E-H型对称分布在A面和B面。仿真模型如图6所示。
对于四馈口,主要研究馈口的分布位置对腔内场分布的影响,设计3个方案:(1)四馈口两两分布在A面和B面,且对称分布的两馈口采用E-E 型分布;(2)四馈口两两分布在A面和B面,且对称分布的两馈口采用H-H型分布;(3)四馈口两两分布在A面和B面,且对称分布的两馈口采用E-H型分布,同侧的两馈口,一个E型,一个H型。仿真模型如图7所示。
4 仿真建模
选择solution type为modal,设置单位为mm。

图6 单馈口和两馈口分布图
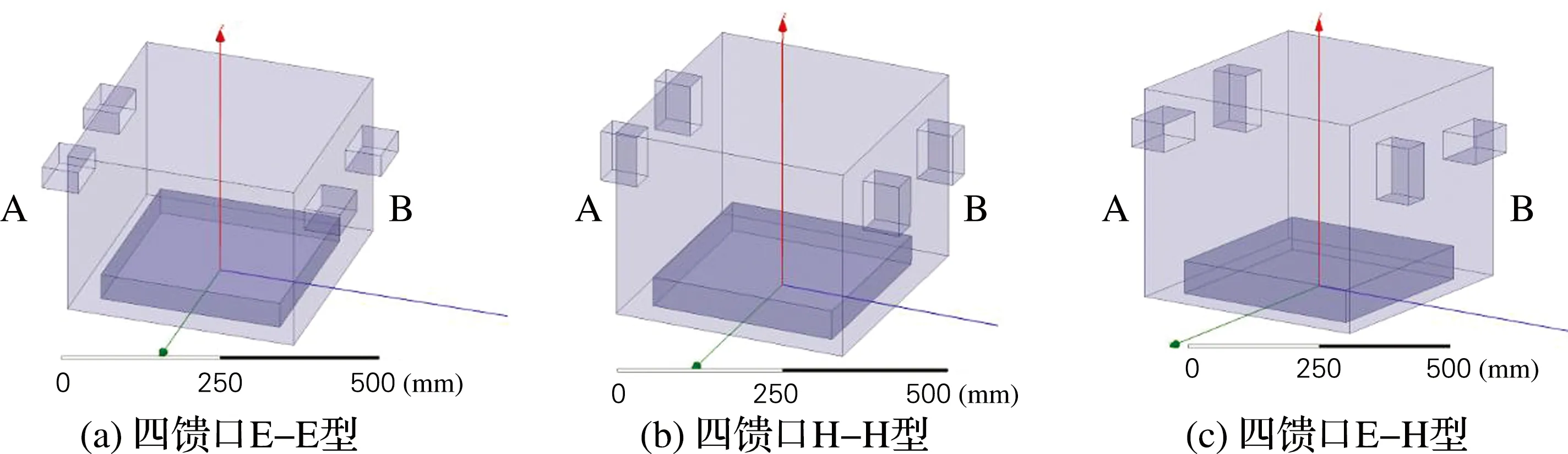
图7 四馈口分布图
微波加热中,常用的磁控管频率为2.45和0.915 GHz。在需要的功率不大,或者材料的厚度不大的情况下选择2.45 GHz的频率,大功率或加热厚物料时选择0.915 GHz,实验模型中使用的磁控管的功率为2.45 GHz,额定功率为800 W。根据谐振腔的尺寸,确定微波馈口端使用BJ-26型波导,内壁尺寸为86.36 mm×43.18 mm。
设置频率为2.45 GHz后,软件自动划分网格,采用默认的网格划分。
谐振腔采用软件默认的真空腔,介电常数为1;内部待加热介质介电常数为17。
实验采用默认的边界条件,即设置整个谐振腔为边界。
单个磁控管功率选择800 W。
5 结果与分析
仿真模型中,选择物料表面所在平面,即z=50 mm为研究对象,分析该平面上的电场强度分布。五种方案中,都存在场强最大的“热点”[18],这是场分布不均匀导致的。单馈口和两馈口分布时,电场强度如表1所示。

表1 单馈口和两馈口场强分布
单磁控管进行加热时,场强不够大,达不到有机质固废对热解的要求,如图8所示。两馈口时,场强较单馈口时明显提高。其中,同侧分布时,场强分布较大,比较均匀;E-E型分布时,场强主要集中在截面中部,向四周散开;H-H型分布时,分布比较均匀,但是场强较小;E-H型分布时,场强在4种分布中最大,且均匀性较好,如图9所示。综上所述,两馈口采用E-H型分布时,场强最大,且分布均匀。

图8 单馈口电场强度分布图
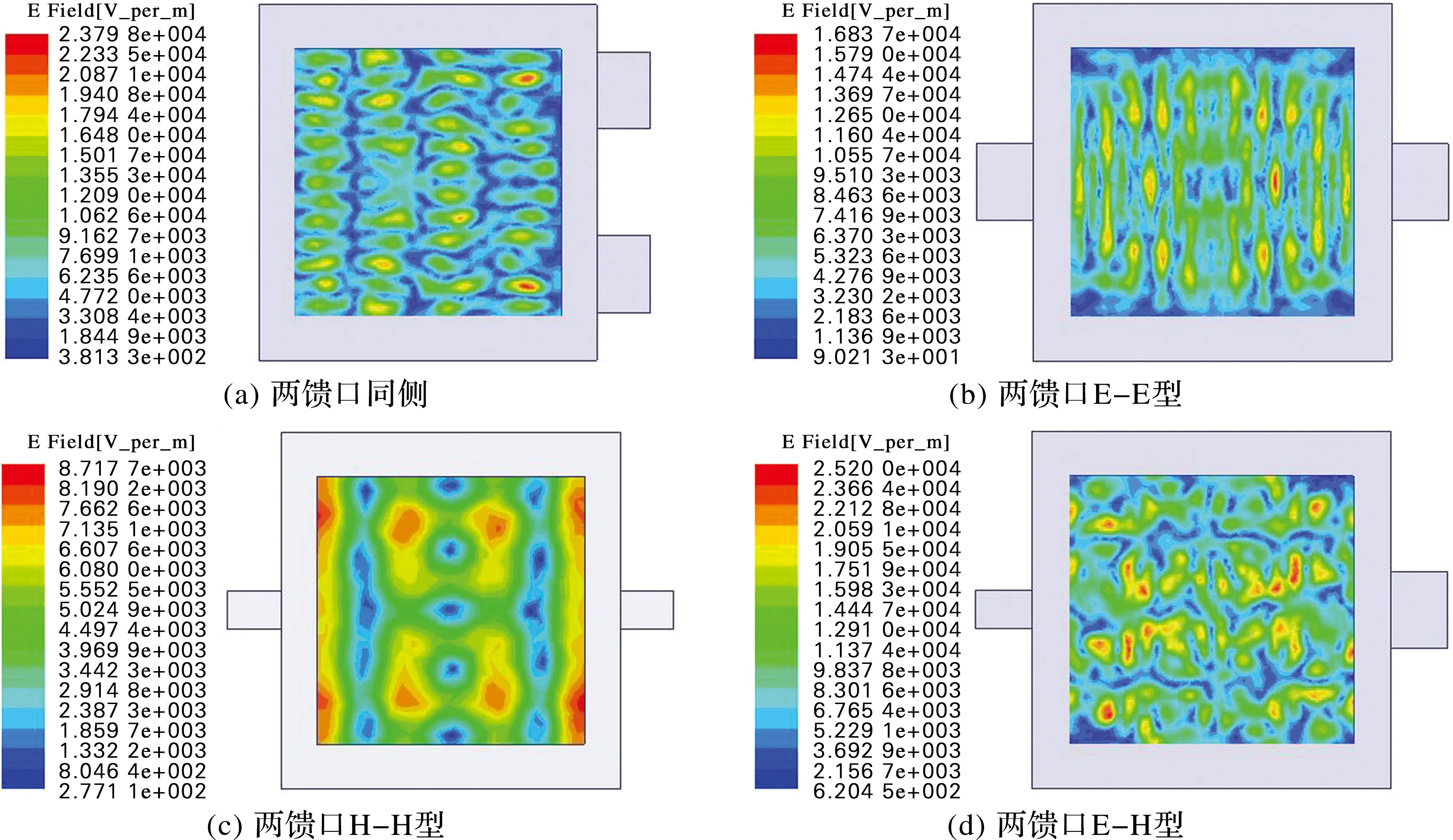
图9 两馈口电场强度分布图
四馈口分布时,电场强度如表2所示。

表2 四馈口场强分布
四馈口E-E型分布时,有几处场强明显高于截面中的其他位置,且其他位置场强较低,场分布均匀性较差;H-H型分布时,截面场强高于E-E型分布,但是依然存在分布均匀性不好的问题;E-H型分布时,除几处“热点”外,场强分布均匀,且整体场强较高,明显优于E-E型和H-H型分布,如图10所示。
6 结 论
基于微波技术波导理论,对微波热解炭化炉谐振腔内电磁场的分布进行了理论分析和仿真,理论分析和仿真结果一致。采用多馈口分布时,腔体内电场强度明显高于单馈口分布的情况;采用两馈口分布和四馈口分布时,E-H型分布都明显优于E-E型分布和H-H型分布;同时,也存在两馈口E-H型分布腔体内部电场强度高于四馈口E-E型分布和H-H型分布。
因此,馈口数目的增加不一定会提高微波炉谐振腔内场强大小,因为馈口位置分布不合理会导致微波在腔内产生干扰和损耗;多馈口分布中,E-H型分布优于E-E型分布和H-H型分布,是一种最优分布方案。
[1] 徐国华,隋玉柱,魏玉西.城市垃圾问题及处理对策[J].环境科学与管理,2006,31(3):29-31.
[2] 张益.我国生活垃圾处理技术的现状和展望[J].环境卫生工程,2000,8(2):81-84.
[3] 李国刚,曹杰山,汪志国.我国城市生活垃圾处理处置的现状与问题[J].环境保护,2002(4):35-38.
[4] OSEPCHUK J M. A history of microwave heating applications[J]. IEEE Transactions on Microwave Theory and Techniques, 1984, 32(9): 1200-1224.
[5] METAXAS A C, MEREDITH R J. Industrial microwave heating[M]. London: Peter Peregrinus, 1983.

图10 四馈口电场强度分布图
[6] BUDAFN V L, CLARK J H, LANIGAN B A, et al. The preparation of high-grade bio-oils through the controlled low temperature microwave activation of wheat straw[J]. Bioresource Technology, 2009, 100(23): 6064-6068.
[7] WAN Y Q, CHEN P, ZHANG B, et al. Microwave-assisted pyrolysis of biomass: catalysts to improve product selectivity[J]. Journal of Analytical and Applied Pyrolysis, 2009, 86(1): 161-167.
[8] LEI H W, REN S, JULSON J. The effect of reaction temperature and time and particle size of corn stover on microwave pyrolysis[J]. Energy and Fuels, 2009, 23(6): 3254-3261.
[9] YAGMUR E, OZMAK M, AKTAS Z. A novel method for production of activated carbon from waste tea by chemical activation with microwave energy[J]. Fuel, 2008, 87(15/16): 3278-3285.
[10] ROBINSON J P, KINGMAN S W , BARRANCO R. Microwave pyrolysis of wood pellets[J]. Industrial and Engineering Chemistry Research, 2010, 49(2): 459-463.
[11] 王立华,林琦.热解温度对畜禽粪便制备的生物质炭性质的影响[J].浙江大学学报(理学版),2014,41(2):185-190.
[12] 张伟燕,刘友春.多模微波加热谐振腔的建模与仿真[J].真空电子技术,2013(5):22-25.
[13] BRESSAN F, DUGHIERO F, BULLO M, et al. Efficiency optimization of a two-port microwave oven: a robust automated procedure[J]. Compel International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2015, 34(4): 1213-1228.
[14] 张景强,王祺,郭建烨,等.陶瓷砂轮微波烧结炉腔内馈口影响仿真研究[J].金刚石与磨料磨具工程,2017,37(5):69-73.
[15] 陈华,张利波,彭金辉,等.单模谐振腔的负载特性对场分布的影响分析[J].昆明理工大学学报(自然科学版),2013,38(2):69-73.
[16] 王飞.基于HFSS仿真技术制取焦糖色素的微波炉优化设计研究[D].广州:华南理工大学,2010.
[17] 冯彤,高冬平,丁海兵,等.多模谐振腔中的微波加热仿真与实验研究[J].真空电子技术,2016(4):47-50.
[18] 谢处方,饶克谨.电磁场与电磁波[M].北京:高等教育出版社,1999.

