带壁厚偏差的无缝钢管推压-拉拔复合缩径
刘 超 王连东 刘 恒 高 缘 王志鹏
1.燕山大学车辆与能源学院,秦皇岛,066004 2.河北机电职业技术学院,邢台,054000
0 引言
缩径管件主要采用推压缩径方法制造,分为无芯轴的自由推压缩径和芯轴推压缩径两种方式[1]。采用自由推压缩径,模具结构简单,生产效率高,但壁厚增加量较大[2],而且缩径后管件端部存在翘曲[3],存在较大的残余应力,易造成轴向开裂[4]。采用芯轴推压缩径,虽可减小壁厚增加量,但传力区轴向应力过大,易失稳起皱[5]。为解决大变形缩径问题,王连东等[6]提出了推压-拉拔复合缩径新工艺,即缩径前将芯轴推入管坯内部,缩径凹模由管端向内部工进的同时,芯轴以大于管坯的伸长速度由管坯内部向端部拉出。大变形缩径一般采用热轧无缝钢管,其价格相对较低,但管坯壁厚存在较大偏差。壁厚偏差势必对管坯缩径成形产生影响,宋希亮[7]对无缝钢管双向等长自由缩径进行了有限元模拟及试验,结果表明,较大的初始壁厚偏差可能引起管坯周向起皱及轴向开裂等现象;陈国强[4]在对小型汽车桥壳所用无缝钢管进行双向等长自由缩径时发现:壁厚偏差大的管坯,在第二次或第三次缩径后,管端出现轴向开裂。对于大变形推压-拉拔复合缩径,成形过程中管坯内部的芯轴向外拉拔,其成形机理与自由缩径不同,管坯的壁厚偏差对成形的影响也比自由缩径复杂,但目前尚未见报道,工艺也未见实际应用。
1 无缝钢管测量及几何模型的建立
1.1 无缝钢管测量
某载重6.5 t胀压成形汽车桥壳初始管坯选用热轧无缝钢管(GB 17395—2008),单根总长为11 700 mm,外直径为219 mm,理论壁厚为7.5 mm。随机抽取9根钢管测量壁厚分布:①将钢管放置在测量平台上,在外表面沿长度方向划出4条纵向线,每条纵向线周向间隔90°。②从钢管前端开始,沿长度每间隔300 mm划出6条周向线,每条周向线代表一个横截面外轮廓,依次记为L1,L2,…,L6截面;在钢管中间及后端每间隔300 mm划出 6条周向线,由前至后,依次记为 L7,L8,…,L18截面,共得到72个测量节点。③针对每个节点,使用超声波壁厚测量仪(MT160)测量壁厚3次,取最小值为测量节点的壁厚。3根较典型钢管的壁厚测量结果见表1。④针对每根钢管72个节点的壁厚测量值,取其算术平均值作为平均壁厚t0,找出最大壁厚tmax与最小壁厚tmin,并计算出最大正偏差δu=tmax-t0、最大负偏差δd=tmin-t0。
分析表1中的测量结果,发现以下现象:①钢管壁厚存在较大的偏差,最大正偏差δu与最大负偏差δd的绝对值差值较小。例如001钢管的t0=7.65 mm,δu=0.34 mm,δd=-0.32 mm;002钢管的t0=7.68 mm,δu=0.51 mm,δd=-0.48 mm;003钢管的t0=7.70 mm,δu=0.39 mm,δd=-0.41 mm。②壁厚差值较大的同一截面上,最大壁厚、最小壁厚节点间隔180°。例如001钢管的截面L16上的90°节点为最大壁厚处(tmax=7.99 mm),与之相对的270°节点为最小壁厚处(tmin=7.33 mm)。002钢管的截面L15与003钢管的截面L7上,亦有同样规律。③沿长度方向上,壁厚分布无明显规律。比如在90°纵向线上,001钢管的tmin=7.68 mm、tmax=7.99 mm;002钢管的tmin与tmax分别为 7.69 mm、8.19 mm;003钢管的tmin与tmax分别为7.65 mm、8.09 mm。
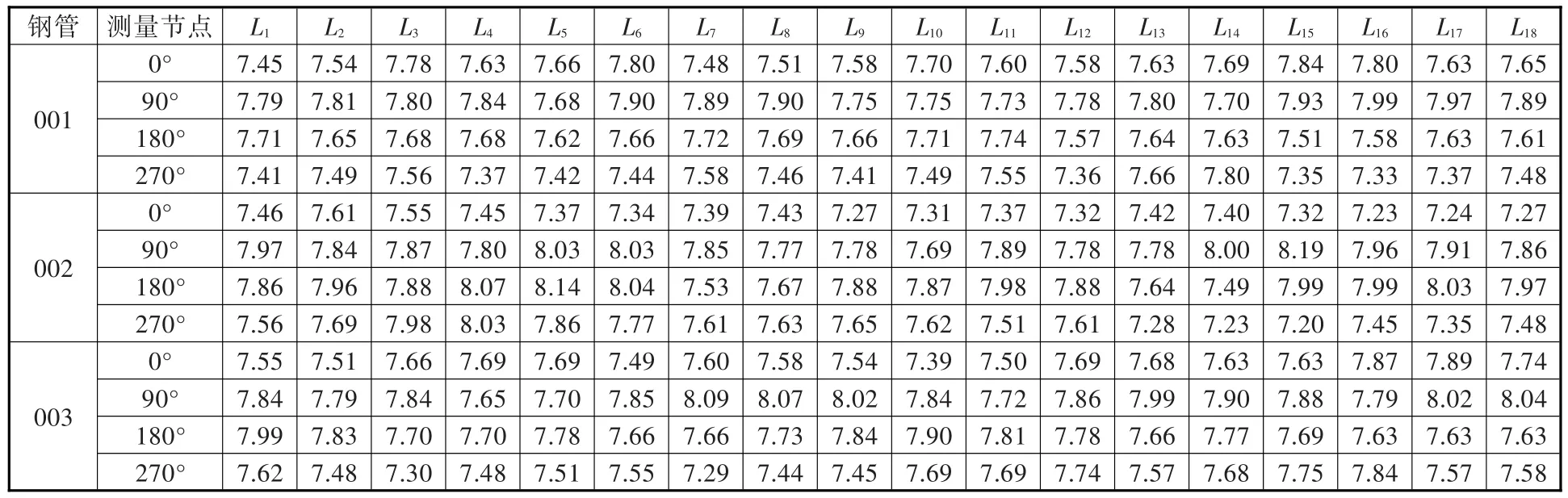
表1 无缝钢管壁厚测量结果Tab.1 Wall thickness of seamless steel tube mm
1.2 带壁厚偏差管坯几何模型的建立
建立带壁厚偏差的管坯几何模型。做以下假设:①管坯长度方向壁厚无偏差,即沿同一条纵向线,壁厚相同。②管坯周向壁厚的最大正偏差与最大负偏差之和为零。③管坯内外表面皆为圆柱面。横截面上外表面圆的半径为R1,圆心为O1,内表面圆的半径为R2,圆心为O2,R1与R2的差值即平均壁厚t0。④横截面上,内表面圆心O2位于外表面圆心O1的正下方,两者之间的偏移量δ即最大正偏差、最大负偏差的绝对值,则最大壁厚(厚壁侧)位于正上方,tmax=R1-R2+δ;最小壁厚(薄壁侧)位于正下方,tmin=R1-R2-δ。
2 管坯推压-拉拔复合缩径力学模型
依据图1中的带壁厚偏差管坯的几何模型,建立其推压-拉拔复合缩径的力学模型,过0°、180°的纵向截面图见图2。管坯外表面为半径R1的圆柱面,其轴线为O1O1;管坯内表面为半径R2的圆柱面,其轴线O2O2位于轴线O1O1正下方,两者间距即轴向偏移量δ。管坯厚壁侧壁厚为t0+δ,薄壁侧壁厚为t0-δ。缩径凹模的轴线与轴线O1O1重合,凹模半锥角为α,过渡圆角为R,凹模出口处定径区的直径为dm。芯轴的外直径为di,其轴线亦与轴线O1O1重合。
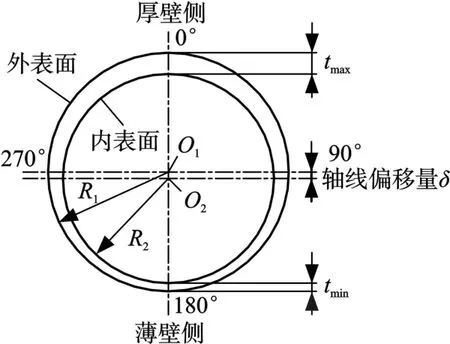
图1 壁厚偏差管坯几何模型Fig.1 Geometric model of tube blank with wall thickness deviation
厚壁侧管坯缩径后定径区外表面与凹模出口处内壁接触,受到法向应力σn2与切向摩擦应力τ2的作用,内表面与芯轴外壁接触,受到法向应力σn3与切向摩擦力τ3的作用,τ3与τ2的方向相反。当轴线偏移量δ达到一定值时,薄壁侧管坯缩径后定径区外表面与凹模出口处内壁不接触,内表面与芯轴外壁接触,受到法向应力σn4与切向摩擦应力τ4的作用,τ4与芯轴外拉的方向相同。

图2 管坯推压-拉拔缩径力学模型Fig.2 The mechanical model of tube pushing-pulling necking
在管坯传力区截面上,存在推压力Fc,质点单元近似处于单向压应力状态。由定径区薄壁侧、厚壁侧的应力状态可初步确定管坯传力区厚壁侧的压应力σρ1的绝对值大于薄壁侧管坯的压应力σρ2的值,且随着内外表面轴线δ的增大,σρ1与σρ2的差值增大,当δ增大到一定值时,厚壁侧区域可能由于σρ1过大而引起失稳起皱。
在锥模减径区,壁厚方向的应变为拉应变,其值主要取决于缩径变形程度及锥模与管坯之间的摩擦因数。在锥模减径区与定径区过渡处,厚壁侧、薄壁侧壁厚方向的拉应变近似相等,即壁厚增加率近似相等,但厚壁侧与薄壁侧的壁厚差值大于初始管坯的壁厚差值2δ。在定径区,由于存在芯轴,减径后的管坯发生挤压变形,壁厚有所减小,同时长度有所增加。厚壁侧的挤压变形程度大于薄壁侧,致使薄壁侧总的壁厚增加率大于厚壁侧总的壁厚增加率,而且随着初始管坯壁厚偏差δ的增大,薄壁侧与厚壁侧的壁厚增加率的差值越大。
3 推压-拉拔复合缩径有限元模拟
3.1 研究对象
以某载重6.5 t胀压成形汽车桥壳第一道次推压-拉拔复合缩径工艺为例,见图3。初始管坯选用热轧Q345B无缝钢管,长度L0=1380 mm,外直径为219 mm,理论壁厚t0为7.5 mm,保留中间传力区长度456 mm的部分不变形,对其两端进行缩径;缩径凹模半锥角α=23°,内直径dm=190 mm,凹模锥面与出口区的圆角半径R=30 mm;芯轴外直径di为173.5 mm;管坯缩径的径向变形量为13.24%。

图3 第一道次复合缩径工艺图Fig.3 The first pass of pushing-pulling necking
选取初始管坯样件进行拉伸试验,得到管坯材料的真实应力-应变关系为σ=900ε0.2,屈服极限为355 MPa,强度极限为620 MPa,弹性模量E=210 GPa,密度 ρ=7 800 kg/m3,泊松比 μ =0.3,硬化指数n=0.2,延伸率为21%。
3.2 有限元模型
在ABAQUS中建立1/4有限元模型,见图4。在管坯的中间横截面与纵向截面上分别设置对称约束;管坯与模具的网格单元都采用C3D8R;缩径凹模、芯轴与夹持模都设定为刚体;缩径凹模与管坯间建立刚-柔接触,其接触动摩擦因数设为0.10,芯轴与管坯间建立刚-柔接触,其接触动摩擦因数设为0.12;缩径凹模工进位移量为462.0 mm,芯轴外拉位移量为52.5 mm。
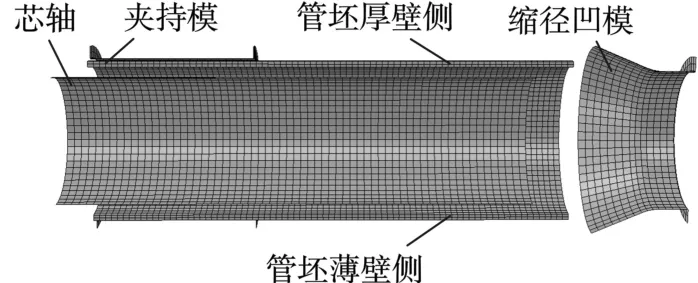
图4 仿真模型Fig.4 FEM simulation model
3.3 模拟结果及分析
设定轴线偏移量δ分别为0.50 mm、0.40 mm、0.30 mm、0.20 mm、0.10 mm、0(周向最大壁厚偏差分别为平均壁厚的13.33%、10.67%、8.00%、5.33%、2.67%、0%)进行仿真分析。
偏移量δ=0.50 mm时初始管坯的模拟结果见图5,管坯传力区厚壁侧出现起皱失稳,起皱处最大半径为111.73 mm;轴向应力呈非对称分布,传力区厚壁侧轴向压应力极大值σρ1=365.45 MPa,达到屈服极限,而薄壁侧 σρ2=97.38 MPa,远小于σρ1;薄壁侧管端出现明显翘曲,管端半径为96.45 mm,翘曲高度为2.03 mm。
偏移量δ=0的缩径结果见图6,管端翘曲量微小,且轴向应力呈轴对称分布。
对不同偏移量的管坯缩径后的几何参数、传力区轴向压应力进行测量,其测量值见表2。
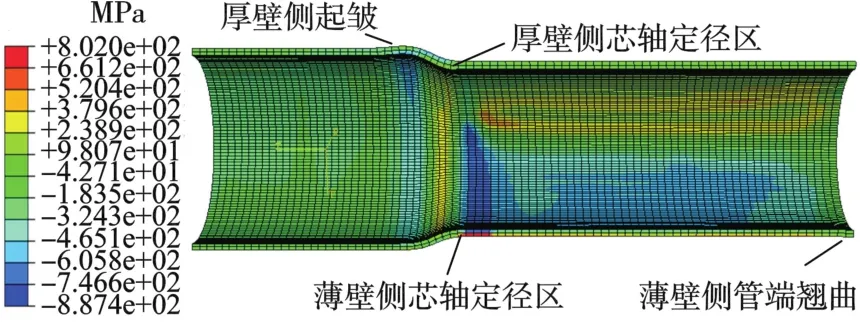
图5 偏移量δ=0.50 mm时模拟结果Fig.5 Simulation results ofδ=0.50 mm
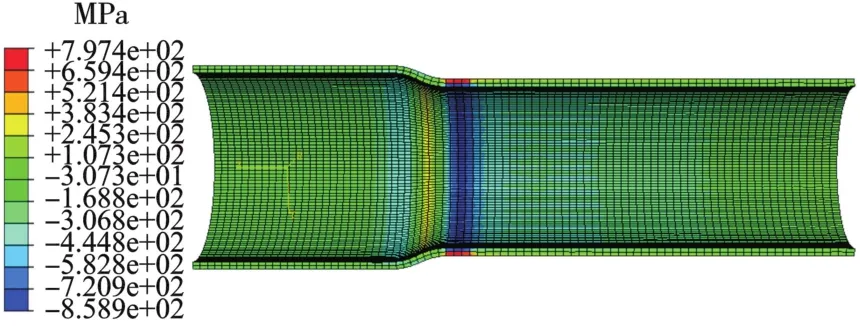
图6 偏移量δ=0时模拟结果Fig.6 Simulation results ofδ=0
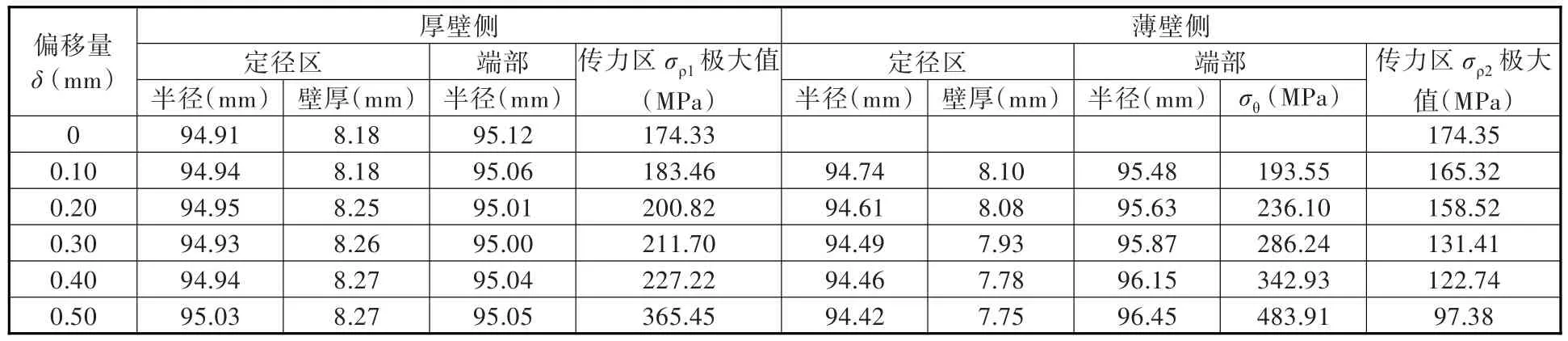
表2 不同偏移量δ模拟结果Tab.2 Simulation results of differentδ
以上有限元模拟结果表明:①从壁厚增加率来看,薄壁侧大于厚壁侧。偏移量δ为0.50 mm、0.30 mm、0.10 mm的管坯缩径后,薄壁侧壁厚增加率分别为10.71%、10.14%及9.46%,厚壁侧壁厚增加率分别为3.38%、5.90%及7.63%。周向最大壁厚偏差分别由1.00 mm、0.60 mm、0.20 mm降为0.52 mm、0.33 mm、0.08 mm,纠正壁厚偏差效果显著。②随着δ的增大,传力区厚壁侧与薄壁侧的压应力差值增大。传力区薄、厚壁侧轴向压应力极大值随δ的变化曲线见图7,当δ=0.30 mm时,厚壁侧的压应力σρ1=211.70 MPa,薄壁侧的压应力 σρ2=131.41 MPa,两者差值为 80.29 MPa;当δ=0.50 mm时,厚壁侧的压应力 σρ1=365.45 MPa,薄壁侧的压应力 σρ2=97.38 MPa,两者差值增至 268.07 MPa。当 δ≥ 0.40 mm时,σρ1急剧增大。③随着δ的增大,薄壁侧管端翘曲量增大,同时管端周向残余拉应力σθ增大。当δ由0.10 mm增大至0.50 mm,薄壁侧管端翘曲高度由0.74 mm增大至 2.03 mm,管端 σθ由 193.55 MPa增至483.91 MPa。
进一步模拟发现:δ>0.44 mm时,传力区厚壁侧σρ1大于屈服极限,管坯出现失稳。管坯的周向最大壁厚偏差为0.88 mm,为平均壁厚的11.73%。
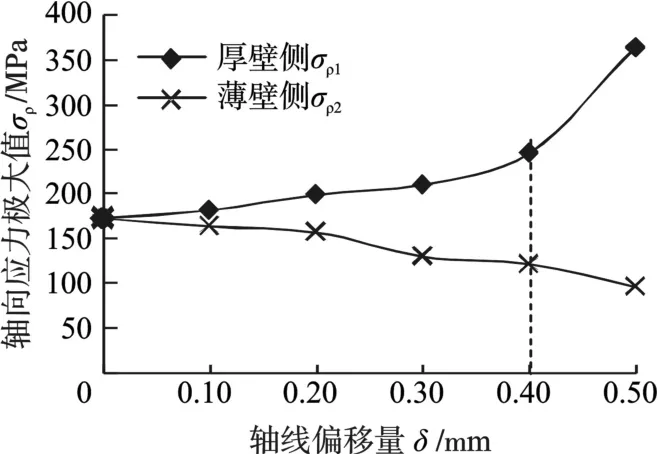
图7 不同壁厚偏差时传力区轴向应力变化曲线Fig.7 Axial stress of different wall thickness deviation
4 生产性试验
4.1 缩径模具
某载重6.5 t胀压成形汽车桥壳第一道次推压-拉拔复合缩径在THP63-200型三向液压机上进行,推压-拉拔复合缩径模具见图8,左缩径凹模6、右缩径凹模11分别固定于左支撑筒5、右支撑筒12上,左右支撑筒分别固定于液压机左滑块4、右滑块13上,左右缩径凹模半锥角均为23°,出口区内直径dm=190 mm,凹模锥面与出口区的圆角半径R=30 mm;左芯轴7、右芯轴10分别与液压机左右中心活塞相连,左右芯轴外直径di=173.5 mm;上夹持模2、下夹持模8分别固定于上模座3、下模座9上,上模座与液压机上滑块1相连,下模座固定于液压机工作平台上。

图8 推压-拉拔复合缩径专用液压机与模具Fig.8 Equipment and die of pushing-pulling necking
4.2 初始管坯
按图3的工艺选取3根平均壁厚较接近而壁厚偏差不同的无缝钢管,编号分别为101、102及103,平均壁厚依次为7.52 mm、7.58 mm及7.56 mm,周向最大壁厚偏差依次为1.03 mm、0.51 mm、0.35 mm(最大壁厚偏差分别为平均壁厚的13.70%、6.73%、4.63%)。管坯壁厚的测量方法同前,为简化测量工作,仅在初始管坯右端从端部向内选取4个横截面,间隔为100 mm,截面1距管坯右端100 mm。
对3根管坯进行推压-拉拔复合缩径缩径试验,缩径时,缩径凹模工进位移量为462.0 mm,芯轴向外拉拔的位移量为52.5 mm。缩径凹模与管坯间使用乳化液进行润滑,其接触动摩擦因数为0.10,芯轴与管坯间不润滑,其接触动摩擦因数为0.12。
4.3 试验结果
101管坯缩径后,传力区出现明显起皱失稳,见图9,管坯起皱处最大外直径为256.50 mm,定径区外直径为189.72 mm,管端外直径为190.16 mm。管坯右端缩径直臂区长度为458.6 mm,伸长量为34.6 mm。101管坯缩径前后,周向最大壁厚偏差皆在截面2上,见表3。缩径后,周向最大壁厚偏差由1.03 mm减至0.54 mm(减小了47.57%),与有限元模拟规律基本一致;缩径后,管坯平均壁厚由7.52 mm增至8.15 mm(增大了8.38%);缩径后,截面2上的最小壁厚处(180°测量点)的壁厚增大率为10.42%,大于最大壁厚处(0°测量点)的3.07%;缩径凹模推力与芯轴拉力分别为1380.6 kN、674.8 kN。

图9 101管坯Fig.9 No.101 Tube
102、103管坯缩径后,无起皱现象,外直径尺寸精度高,管端平直,见图10。两管定径区外直径分别为189.78 mm、189.64 mm,管端外直径分别为189.88 mm、189.70 mm。两管右端缩径直臂区长度分别为462.4 mm、460.6 mm,伸长量分别为38.4 mm、36.6 mm。
102管坯的截面3与103管坯的截面4为周向最大壁厚偏差截面,见表3。缩径后,两管周向最大壁厚偏差分别由0.51 mm、0.35 mm减至0.27 mm、0.18 mm;缩径后,102、103管坯平均壁厚分别由7.58 mm、7.56 mm增至8.24 mm、8.13 mm;缩径后,最大周向壁厚偏差截面上最小壁厚处的壁厚增大率分别为11.09%、9.05%,大于最大壁厚处的7.29%、6.45%;102管坯的缩径凹模推力与芯轴拉力分别为1110.5 kN、582.6 kN,103管坯的模具力略有减小,分别为989.1 kN、527.8 kN。
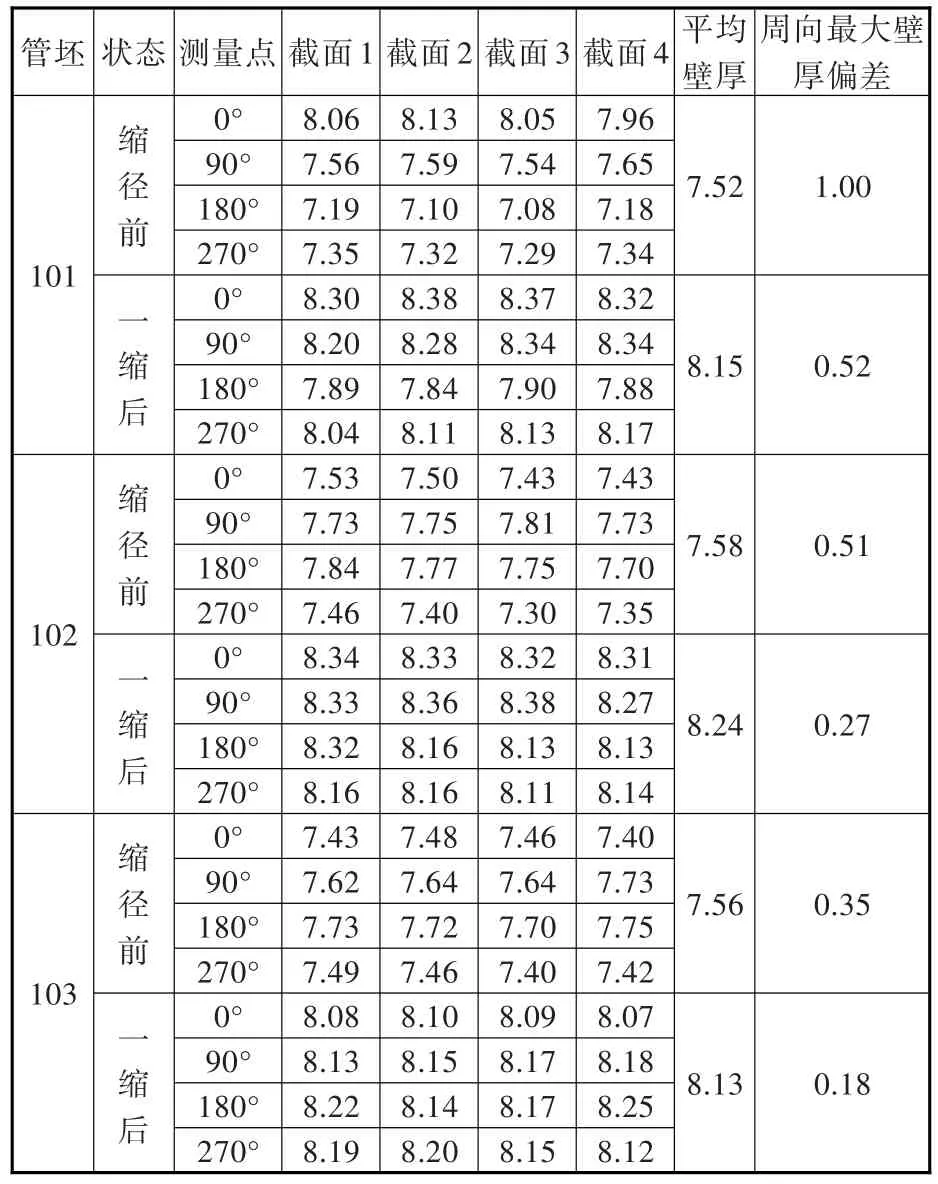
表3 缩径前后管坯壁厚变化Tab.3 Wall thickness of tube after necking mm

图10 103管坯Fig.10 No.103 Tube
相比103管坯,101、102管坯的缩径凹模推力分别增大了39.58%、12.27%,芯轴拉力分别增大了27.85%、10.38%,表明壁厚偏差较大的管坯,缩径时的模具力较大,实际管坯与有限元模型有差别,但壁厚偏差对模具力的影响与有限元模拟趋势一致。
5 结论
(1)变形后,壁厚增加率方面,薄壁侧管坯大于厚壁侧管坯;轴向压应力方面,管坯传力区厚壁侧大于薄壁侧;随着壁厚偏差的增大,厚壁侧的轴向压应力随之增大,当偏差增大到一定值时,传力区厚壁侧可能由于压应力过大而引起失稳起皱。
(2)随着δ的增大,传力区厚壁侧与薄壁侧的压应力差值增大;随着δ的增大,缩径凹模推力、芯轴拉力增大;随着δ的增大,薄壁侧管端翘曲量及管端周向残余拉应力增大;管坯的周向最大壁厚偏差小于平均壁厚的11.73%,传力区不失稳。
(3)通过试验成功试制出缩径样件,壁厚与模具力的变化规律与有限元模拟结果趋势一致。
[1] SADOK L,KUSIAK J,PACKO M.State of Strain in the Tube Sinking Process[J].Journal of Materials Processing Technology,1996,60(1/4):161-166.
[2] PENG Junyang,FU Yuan,CHEN Jingsong,et al.Experimental Investigation on Thickness Changes during Necking Process[J].Journal of Plasticity Engineering,2012,19(3):60-63.
[3] WANG Liandong,ZHAO Shiyan,GAO Pengfei,et al.Analysis of Buckling in Push-sinking and Its Influence Factor[J].Journal of Plasticity Engineering,2005,12(3):76-79.
[4] CHEN Guoqiang.Study on Half-sliding Hydroforming of Automobile Axle Housings[D].Qinhuangdao:Yanshan University,2014:89-91.
[5] HONG Chunteng,BING Yanteng.An Optiming Process Design for Sinking with the Thin-wall Cylindrical Cup[J].Applied Mechanics and Materials,2014,456:22-27.
[6] WANG Liandong,LIANG Chen,MA Lei,et al.The Bilateral Reverse Mandrel Reduction Die and Technology of Tube:China,201310191757.9[P].2015-05-13.
[7] SONG Xiliang.The Test Research of the Wall Thickness Changing of Seamless Tubes during Necking Process with Equal Length at Both Sides[J].Modern Manufacturing Engineering,2012,379(4):84-88.

