长直密绕载流螺线管磁场的一种算法

刘保义

（天水师范学院 电子信息与电气工程学院，甘肃 天水 741001）

在一般普通物理学中，[1-2]对长直载流螺线管外部磁场，认为无限长直，且是细导线均匀密绕，给出的结论是管外磁感强度很小，可以看作零。应该说，这些结论是在近似条件下得出的，是一种近似值，与绝对等于零性质不同。有一些文献对此进行了探讨，文献[3]、[4]论证相对较深刻，但对电流密度的认识和正交分解不准确，对电流强度得出并应用了I=Icosα+Isinα这样的结论，这显然是不正确的，因为电流强度是标量而不是矢量。本文精确分析长直均匀密绕载流螺线管上电流的分布，给出计算螺线管外部磁场的一种简明方法。

1 长直载流螺线管电流的分解

长直载流螺线管是指均匀密绕在长直圆柱面上的螺旋形线圈，如图1所示，设其半径为R，长度为L，螺旋线切线方向与圆周平面的夹角为α，螺距为h，每单位长度有线圈n匝，通过导线的电流强度为I，当L＞＞R时，可视为无限长载流螺线管。取螺线管中心轴线为z轴，z轴正方向与载流导线电流成右手螺旋关系，x轴沿圆周半径方向向外，如图2所示。

电流密度是一个矢量，该矢量在导体中各点的方向代表该点电流的方向，其数值等于通过该点单位垂直截面的电流强度，[1]电流强度与该点电流密度的关系为：

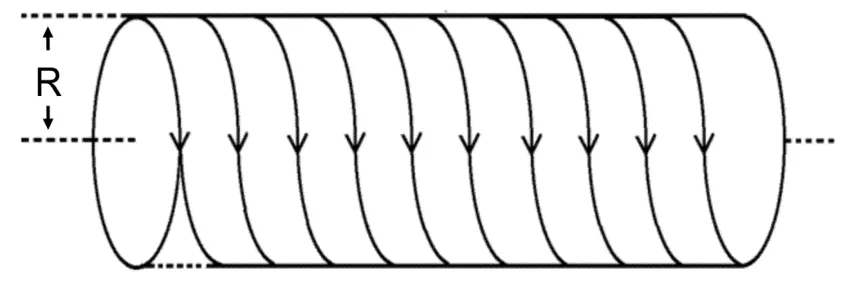
图1 载流长直螺线管

图2 螺线管电流密度的正交分解

而其中d为导线半径。载流螺线管的导线可看作圆柱螺旋线，电流密度方向也就沿圆柱螺旋线的切线方向。建立柱坐标系在选取的电流元处单位矢量沿圆半径向外，沿圆周切线方向，与轴线平行。电流密度在柱坐标系中正交分解得

-→某点电流密度在过该点处的密切平面内，所以在eρ方向的分量为零。切向电流密度与轴向电流密度大小为

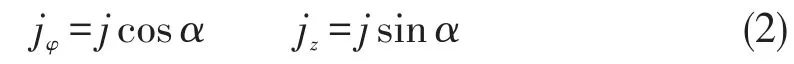
法线方向与电流方向相同，沿圆柱螺旋线的切线方向，大小为导线截面，把它在柱坐标系正交分解

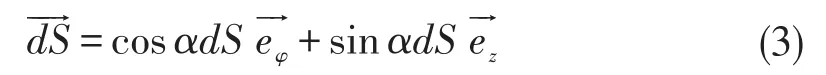
即有

所以

积分得出圆环电流与轴向电流

上两式相加得出

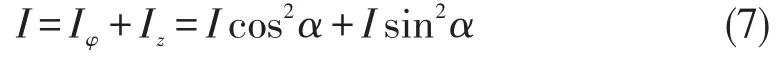
上式表明，螺线管上沿圆柱螺旋线方向的电流，可看作沿圆周切线方向的圆环电流与轴向电流两个分电流并联组成，这也符合电流的叠加原理。由三角函数关系可得出

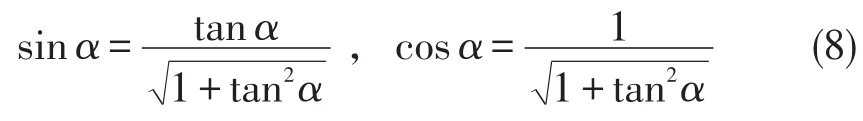
由几何关系可知，tanα=h(2πR)，所以有

这样就得出两个分电流的大小，即圆环电流和轴向电流为

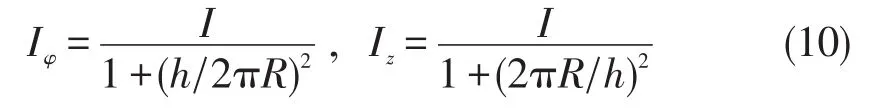
若单位长度有n匝线圈，总匝数为N，螺线管长为L，则有 n=N/L，又L=Nh，所以有h=1/n，则（10）式可表为

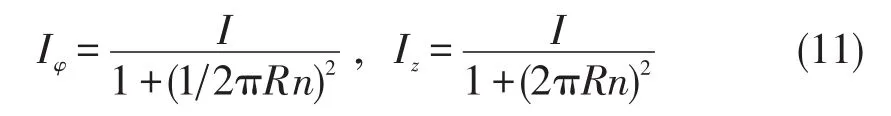
对密绕螺线管（相邻导线紧密切靠在一起），螺距h与导线直径2d的几何关系是：sinα=2d(2R)，由（6）式把圆环电流和轴向电流还可表述为

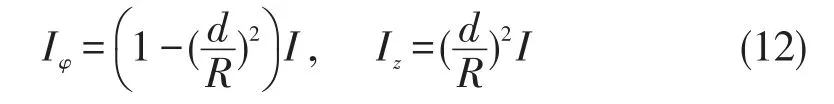
当R＞＞d时，这是一种极限情况，也是我们求解长直载流密绕螺线管磁场常用的方法，数学方法简单，与实际情况接近。

2 长直载流螺线管磁场的求解

螺线管上沿圆柱螺旋线方向的电流正交分解为圆环电流与轴向电流，则磁场也看作是圆环电流与轴向电流分别产生并叠加形成。圆环电流线密度为：nIφ=nIcos2α，圆环电流在管外的磁场为零，在管内形成匀强磁场，方向沿轴向，与电流成右手螺旋关系，大小为

当R＞＞d时，由上式可得出Bzmax=μ0nI，与我们常见的结论一致。

轴向电流可看作均匀分布在螺线管外面，形成一个圆筒电流，电流密度为

具有轴对称性，由环路定理可知，此电流在螺线管内不产生磁场，在螺线管外的磁场与长直载流导线形成的磁场性质相同，关系式为

在螺线管外表面处，r=R，磁场最强为

螺线管外表面处的磁场强度与管内场强之比

举例计算螺线管外表面处的磁场强度，如果有n=5/cm，R=3cm，上式比值为1.2×10-6，非常小。

3 结 论

从本文可以得知，无限长直均匀密绕载流螺线管的磁场分布为：其管内磁场是由圆环电流所产生，方向沿螺线管轴向，并与圆环电流成右手螺旋关系。其外部磁场是由轴向电流所产生，磁感应强度很小，方向沿圆周切线方向并与轴向电流成右手螺旋关系。尽管管外的磁场趋向于零，但与绝对等于零的性质是不同的，在磁AB效应中，把管外磁场按照绝对等于零对待，是不对的，从（15）式可看到，管外表面附近的场强与螺线管半径成3次方反比关系，当R很小时，螺线管外表面附近的场强并不小。在磁AB效应中，由于电子的波长很短，限制磁场在很小区域内，螺线管半径R不但必须很小，长度还不是无限长，螺线管外表面附近的场强是存在的，不能当作零处理，实际上这就是磁AB效应产生的原因。

[1]赵凯华,陈熙谋.电磁学[M].北京:高等教育出版社,2003.

[2]郭硕鸿.电动力学[M].北京:高等教育出版社,1997.

[3]柳建国,陈钺.长直载流螺线管的磁场的研讨[J].湖南理工学院学报(自然科学版),2010,(3):72.

[4]蔡子勇.长直螺线管磁场的全空间解[J].大学物理,1986,(1).