多维立体探究 让素养落地生根——《多边形的内角和》教学与评析

执教/钱兆兰 评析/刘德宏

【教学内容】

苏教版四年级下册第96～97页。

【教学过程】

一、联系旧知，引入新课

师：同学们，图形是我们数学学习的重要内容，你知道哪些图形？

生：三角形、正方形、长方形……

师：大家说到的一些图形，我们用三角板就可以拼出来（课件逐个出示三角板拼成的部分实图：三角形、长方形、正方形、平行四边形、四边形、五边形……），给我们的三角板越多，拼成的图形形状也就越多（课件出示三角板实物隐退后的抽象图形）

师：像这些由三条或三条以上的线段首尾相接围成的平面图形，它们有一个共同的名字，叫多边形。（板书：多边形）

师：三角形是最简单的多边形。

师：在多边形中我们已经知道三角形的内角和是180°，你想到什么新问题呢？

生：四边形、五边形、六边形等其他多边形的内角和又分别是多少度呢？

师：问题提得真好!是呀，四边形、五边形、六边形等其他多边形它们的内角和又分别是多少度呢？这当中有没有什么规律呢？今天这节课我们一起来研究多边形的内角和。

【评析：学生已经知道三角形的内角和是180°，这是本课教学的知识生长点，“三角板拼图形”不仅让学生感悟图形之间的关系，更顺势引导学生联系旧知自主推理产生疑问，让学生从发现问题、提出问题开始真正经历规律的探究过程，并为接下来的“四边形内角和探究”埋下伏笔。】

二、新课探究

师：我们已经知道三角形的内角和是180°，下面让我们从四边形开始，展开对多边形内角和的研究。课件上正好有几个四边形，你觉得它们的内角和是多少呢？

生：360°。

生：我也觉得是360°。

师：为什么？你是怎样想的？

生：正方形、长方形是四边形，四个角都是直角，4个90°是360°，那么，我想其他四边形的内角和也是 360°。

生：我的想法和他一样。

师：我们可以确定正方形、长方形的内角和是360°（课件在正方形、长方形四个内角处添加直角符号），但其他四边形的内角和到底是不是360°呢？让我们小组合作开始探究。

1.探究活动：小组合作探究四边形的内角和是多少，初步感受分割法。

师：请大家以小组为单位，选择方法来探究“四边形的内角和是不是360°”。

课件出示活动要求：①任选一个四边形作为研究对象，标出其所有内角；②小组商议，确定验证方法后动手实践；③操作完成后，推选代表准备发言交流。

（学生分组探究活动）

师：下面请每个小组将本组的验证方法与结论和大家交流。

生：我们组用量角器分别量出4个角的度数后相加，发现四边形的内角和是360°。

生：我们参考以前学习三角形内角和的方法，把四个角撕下来拼到一起，发现刚好拼成一个周角，我们认为四边形内角和是360°。

生：我们没有量也没有撕，我们小组从刚才用三角板拼图形得到启发，加了一条线把四边形分成两个三角形，再用 180°×2就得出这个四边形的内角和是 360°了。

师：没有量也没有撕，只加一条线，听起来很简单，给大家具体说说。

生：（实物投影）从顶点到相对顶点连一条线将四边形分割成两个三角形，原来的四个内角被分割成了六个角，分别在两个三角形中，三角形的内角和是180°，再用180°×2就求出了四边形的内角和是360°了。

师：“求四边形的内角和”可以转化成“求两个三角形的内角和”（课件将学生展示的再逐步呈现），两个三角形一共六个内角的和就是四边形的内角和，分割、转换是我们学习数学知识时经常用到的重要的数学方法。

师：有结果不是360°的吗?

生：没有。（若有，关注方法及测量误差）

师：那还有不同证明方法吗？

生：没有了。

师：好，我们现在可以确认“任意四边形的内角和都是 360°”。

师：量、撕、分割三种方法，你更喜欢哪种方法？

方法优化：运用“分割法”将多边形分成几个三角形，几个三角形的内角和就是多边形内角和的方法较简单。

【评析：四边形的内角和是探究多边形内角和的第一层面纱，从“自然量”、“ 按需撕”到“尝试分”求和是重要的思维跨越，给足时间、空间，引导学生数形结合，自主思考，小组合作探究初步感知规律，渗透数学思想，发展思维。】

2.探究活动：引导多维思考，自主探究五边形、六边形的内角和，优化分割方法。

师：下面请大家从材料袋中取出老师给大家准备的五边形，求出它的内角和。

（学生自主操作，教师巡视）

（汇报交流）

生：我分割成了3个三角形（教师引导学生感受从任意一个顶点出发分割），180°×3=540°。

生：老师，我和他不同，我分成了四个三角形（教师引导学生感受从边上任意一点出发分割），180°×4=720°。

师：现在出现了两种结果，有没有和这两种都不一样的了？

生：没有了。

师：让我们分别请这两种结果的一位同学作代表，带着他们的图展示给大家看一下，请大家仔细观察，说说你的想法。

（投影展示，学生观察）

生：我认为720°的错了，他多算了角。

生：我也认为720°的错了。

师：他多算了哪里的角呢？请学生上来指一指。

师：是的，他多算了边上新出现的角，那我们只要再用720°-180°就可以得出五边形的内角和是540°。

师：分法不同，角的变化情况就不同，要仔细灵活处理。

师：老师刚刚还看到有同学这样（课件或投影，教师引导学生感受从图形中间任一点到多边形顶点连线分割）将多边形分成了几个三角形，你们看，又该怎样处理呢？

生：他这样分成5个三角形也可以，但中间多出了一个周角，要用 180°×5-360°=540°。

生：对，把中间多出来的角减掉。

师：分法不止一种，请仔细观察“从任意一个顶点出发分割”、“ 从边上任意一点出发分割”、“从图形中间任一点到多边形顶点连线分割”这三种分法，他们分别分了几次？五边形被分成了几个三角形？你觉得哪一种分法在算五边形内角和时更方便？（课件出示）

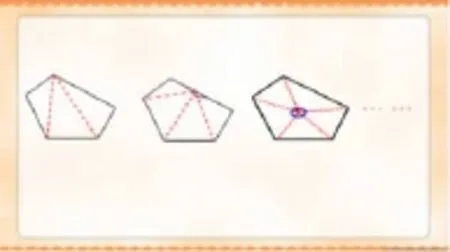
明确：从五边形任意一个顶点出发，分别与它不相邻的所有顶点（2个相对顶点）连线分最方便（不会产生新的角，只是将原来多边形的内角进行了分割）。

师：请你分一分，求出六边形的内角和。

（学生自主连线分割，求六边形的内角和）

汇报交流并明确：

（课件出示）从六边形任意一个顶点出发，分别与它不相邻的3个相对顶点连线，将六边形分割成4个三角形，则六边形的内角和是180°×4=720°。

【评析：揭开四边形的内角和这第一层面纱后，鼓励学生自主迁移，从“任意一个顶点出发分割”、“边上任意一点出发分割”、“图形中间任一点出发分割”这三种分割角度重点对五边形的内角和展开多维立体探究，进一步渗透数学思想。】

3.探究活动：探究其他多边形的内角和，尝试发现规律并小结明确。

师：让我们继续探究其他多边形的内角和。请同学们从材料袋中选一个或自己画一个多边形（六边形以上、小组内争取不同图形），求出它的内角和，并小组填写“表格一”。

（学生自主探究填写）

汇报交流：（板书）

七边形 180°×5=900°

八边形 180°×6=1080°

……

师：大家通过分割又快又好地求出了这些多边形的内角和。接下来请大家再算算五十边形的内角和。

（学生动手画，又放弃）

师：大家怎么不动手了？

生：边数太多，不好画、分。

师：看来，碰上边数较多的图形，分割后算不是最好的方法，我们有必要来找找规律。请大家借助板书，小组完善“表格二”的填写（课件出示“表格二”）。

（学生小组填写表格）

集体交流，完善课件表格填写。

?

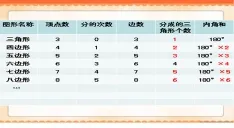
师：请大家仔细观察表格中相关数据,看看能发现什么,在小组里说一说。

（学生观察，小组交流）

集体汇报交流：

（1）多边形的内角和与多边形的顶点个数有关。

n边形n个顶点，任意一个顶点有（n-3）个相对顶点，分（n-3）次，分成（n-3+1）个三角形，n边形内角和为（n-3+1）×180°。

（2）多边形的内角和与多边形的边数有关。

n边形n条边，分成（n-2）个三角形，多边形内角和=（n-2）×180°。

4.立体切换，多维沟通。

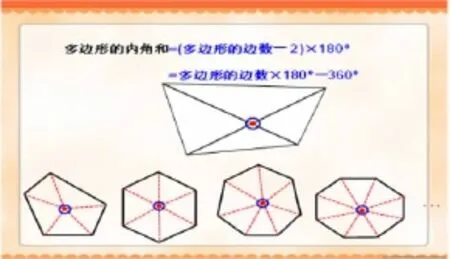
师：用乘法分配律将多边形的内角和公式变一变，（边数-2）×180°=边数×180°-2×180°=边数×180°-360°（课件出示四边形分割图），你又有什么新发现？

说明：“从多边形中间任一点出发分割”比“从多边形任意一个顶点出发分割”总是多出一个周角，只要“边数×180°-360°”即可求出多边形的内角和。“从多边形边上任意一点出发分割”，只要“（边数-1）×180°-180°”即可，（边数-1）×180°-180°=边数×180°-360°

【评析：把握数学本质，创设认知矛盾，激发规律探索需求，引领学生自发、自主探究规律，提升观察、比较、归纳等多项能力。】

三、规律应用

师：现在你能求出五十边形的内角和吗？

生：（50-2）×180°=8640°。

师：n边形呢？

生：（n-2）×180°。

师：一个多边形内角和是1080°，你知道它是几边形吗？

生：1080°÷180°+2=8，八边形。

【评析：应用拓展，帮助学生进一步认识规律，培养运用意识及解决问题意识，提升解决问题的能力，发展核心素养。】

四、回顾感悟探究过程，文化链接

1.回顾感悟探究过程。

师：我们是怎样探索发现多边形内角和规律的？

师：回顾探究过程，你有什么收获？

2.数学文化介绍。

（课件出示“古希腊数学家泰勒斯、欧几里得等人多边形内角和的探索历程”简介）

【评析：引领学生从知识探究过程本身、探究方法及数学思想等多个不同层面回顾感悟，再一次让学生经历探究规律活动的全过程，感悟规律探究的一般方法，提升素养并增加文化积累。】

五、总结提升

师：回顾本节课的学习，你有什么收获？

（引导学生多角度说，相机小结提升）

师：我们的收获不该止于某个规律、公式，掌握探究学习新知、发现规律的方法将会使我们受益终生。

【评析：引领学生多角度对整节课的学习进行回顾小结，培养反思总结能力，从重知识、规律的理解记忆转变为重规律探究方法的感悟。】