基于匹配的异构数据索引方法
梁英飞,童海红,刘 巍(中国航发哈尔滨东安发动机有限公司 信息档案中心,哈尔滨 150066)
20世纪以来,信息化数据以指数规模增长,这使得人们从纷乱复杂的异构数据中迅速有效地得到自己关注的信息变得困难重重,而索引是信息获取过程中最重要的一步。目前,结构化数据和非结构化数据的索引研究已取得重大成果,但单一类型的数据索引已无法满足用户需求,所以研究支持多种类型的数据索引已迫在眉睫[1,14]。
当前形势下的数据环境异常复杂,数据量日益增大。目前,异构数据类型主要包含两种:一种是以关系型数据库为代表的结构化数据;另一种是以文本文档、HTML网页、Email等为代表的非结构化数据。结构化数据的主要查询方式为SQL,非结构化数据的主要检索方式为关键词搜索。随着数据信息化的快速推进,能同时检索多种数据类型的索引已引起人们关注。异构数据索引不同于单一类型的数据索引,它能够支持各种类型的数据检索[1,6-7]。
部分匹配(Partial Match):针对一个由d维向量空间{0,1}d中n个点组成的数据集,给定一个查询x,x包含在d维向量空间{0,1,*}d中,数据集中的点y满足对任意的i,xi≠*有xi=yi,则x与y部分匹配[1,13]。
已有文献已经证明部分匹配问题和子集合查询问题表面上虽然不同,但本质上是等价的。子集合问题定义:给定一个集合U,S是U中n个子集的集合,|U|=m,对一给定的查询集合Q⊆U,若存在P(P∈S),满足Q⊆P,则Q是P的子集[15-16]。
部分匹配和子集合都是数学领域中研究比较广泛的问题,这两个问题在本质上等价,研究点也有很多重合部分。部分匹配问题是很多领域的最基本、最重要的应用问题,如在信息检索领域搜索包含指定关键词集合的文档,像Google,Baidu等,在数据库领域搜索满足等式约束(如“Age=25 and City=Shanghai”)的记录,在IP数据包分类领域中部分匹配也应用广泛。
在信息检索领域按照匹配程度,数据查询的种类主要包括两种:精确匹配查询(Exact Match Query)和部分匹配查询(Partial Match Query)[2]。直观的描述如下:定义一个文档,由一组关键词k1,k2,…,kn构成,(1)精确匹配查询:表示F的所有关键词必须全部匹配才能命中,即查询必须指定文档中所有存在的关键词,例如k1∧k2∧…∧kk;(2)部分匹配查询:只要存在表示F关键词匹配就可命中,即查询中包含一部分指定文档的关键词即可,例如ki∧kj。从目前的信息获取方式来看,用户发布的查询不可能每次都能全部命中数据对象的全部关键词,用户需要更加灵活地发布自己的查询,从这方面看部分匹配更适合异构数据索引的要求[8-12]。
1 部分匹配索引
1.1 部分匹配索引体系结构
本文构建异构数据索引主要分以下几个步骤:首先解决异构性问题,对给定的异构数据源统一数据模型,将来自各个不同数据源的数据统一用本文提出的数据模型表示,形成新的数据集;然后构建索引,针对数据模型中的关键词进行预处理,得到关键词在数据集U中的查询计数,将关键词依照查询计数排序;而后在逐级构建索引时,依然以关键词计数为基础,按照指定的剪枝条件有选择地构建特定数据条目的索引。为了加速索引的构建过程,本文在构建索引时利用了Trie树结构来加速查询的匹配速度,最终按照L1,L2,…Lk的顺序构建部分匹配索引。图1展示了部分匹配索引的体系结构。

图1 部分匹配索引体系结构图
1.2 数据模型
为保证来自不同数据源的各种各样的异构数据能映射到该模型上,本文在研究多个模型的基础之上提出一个较好的数据模型。该模型由三部分组成,可描述为
d::=
(1)
式中:Oid:对象唯一标识符,此字段仅供系统内部使用,对用户不可见;
DTL:文本描述标签,此字段是可变长度的字符串,帮助用户理解对象的具体类型、来源等,便于用户理解和使用对象;
{K1,K2,…Kn}:描述数据对象的关键词集合,例如从文本数据中抽取出来的top-k关键词。
对于非结构化数据,本文采用基于TF-IDF的文章关键词抽取器进行关键词抽取,使用网页爬虫工具LocoySpider抽取网页数据,针对抽取后的数据进行处理后得到本文需要的关键词[3]。对于结构化数据,本文利用文献[4]中的方法得到元组单元,并构建与之相对应的虚拟文档,同样对虚拟文档进行关键词抽取。
每个模型都有各自的查询语言,本文模型也不例外。设U代表数据集,d∈U,基于部分匹配的查询如式(2)所示。
q={k1andk2and … andkp}
(2)
式中k1,k2,…,kk表示关键词,如果q出现在对象d的Keywords中,即存在整数i1,i2,…,ip∈{1,2,…,n}使得
k1=Ki1andk2=Ki2and … andkp=Kip
(3)
成立,则认为查询q与对象d相匹配,从式(3)可以看出查询q仅仅包含了对象d中Keywords的一部分,因此称查询q为部分匹配查询。
对于查询q和数据集U,采用MU(q)表示U中与查询q相匹配的数据对象Oid集合,可表示为MU(q){o1,o2,…,on}。
1.3 部分匹配索引表
针对上面定义的数据模型及查询语言本文设计了部分匹配索引表,它由数据表组成,每张表都有自己的聚簇索引,为了节省表空间并加快检索速度,将倒排文件技术应用到索引表中。本文给部分匹配索引设定两个参数,自然数N和比例因子ε>0,这两个参数由系统管理员设定。为保证响应查询q所耗费的时间与查询结果数|MU(q)|成比例,此处给出一个部分匹配索引的时间限制条件:响应查询q所耗费的磁盘I/O数目应≤max(N,(1,ε)/MU(q)|)。
部分匹配索引表主要包括:
(1)TU(Oid,Description,Keywords)表,带有Oid的聚簇索引;
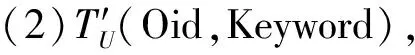
(3)RTU(Rank,Keyword):排序表,数据集中所有关键词按照查询计数顺序存储在此表中。
(4)索引表L1,L2,…,Lk,…,表的确切数目k依赖于数据集U,一般来说都比较小。对于每个k≥1,Lk模式为Lk(Oids,Keyword1,…,Keywordk),一条数据记录Lk({o1,o2,…,on},k1,k2,…,kk)表示所有包含了关键词k1,k2,…,kk的对象集合,即Lk中的Oid集合就是查询qk={k1,k2,…,kk}的查询结果。Lk中存储了针对某些带有k个关键词查询q的所有返回结果。
根据以上定义,部分匹配索引表基本构成如图2所示。

图2 部分匹配索引表
1.4 基于计数的部分匹配索引算法
构建部分匹配索引的难点在于选择哪些查询存储到相应的Lk中。如果把所有的查询都囊括进去,则部分匹配索引过大,既不利于用户检索又耗费了过多的系统资源;如果存储的过少,则会影响用户的查询速度,体现不出索引的优势。下面介绍部分匹配索引的构建标准,即如何选择查询qk插入部分匹配索引的Lk中。Retrival(q)表示由查询q的所有正确查询结果以及一些误报结果(不满足条件也被检索出的数据对象)组成,关键词的查询计数表示当前待查询关键词ki在数据集U中的匹配项的个数,MU(q)表示匹配查询q的U中的数据对象的Oid集合,可表示为MU(q)={o1,o2,…,ok}。
索引的构建从L1开始,为了保证响应查询q1所耗费的磁盘I/O数≤max(N,(1+ε)|MU(q)|),则L1中存储所有|MU(q1)|>N且MU(∅)>(1+ε)|MU(q1)|的一元查询q1,L1包含的关键词都有较高的匹配度,接下来顺序构建L2,L3,…。
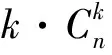
(1)其中Retrival(qk-1)是查询qk的近似结果,且能够获取到;
(2)qk不在Lk中;
(3)|Retrival(qk-1)|>N;
(4) |Retrival(qk-1)|>(1+ε)|MU(qk)|。
若查询qk同时满足上述条件,则将其插入到Lk中,其中(1)和(2)为前提条件,(3)和(4)为插入条件。若qk满足(1)和(2),则这样的qk会被计算,并考察条件(3)和(4),若qk满足(3)和(4),则将qk插入到Lk中。
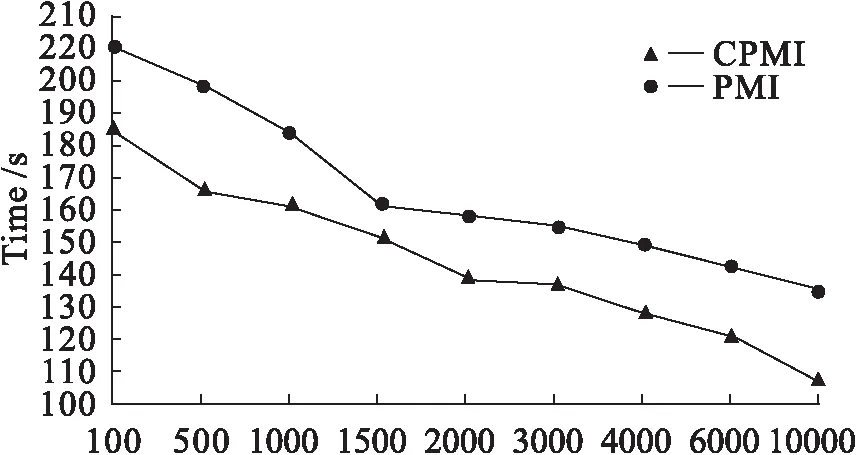
以上是构建部分匹配索引的粗略思想,但不具备实用价值,主要因为其枚举了数据实例中的所有查询,这种枚举做法效率过低。针对这一问题,本文提出一种以关键词的查询计数排序为基础,并充分利用数据挖掘中剪枝思想来构建部分匹配索引的策略,本文称之为基于计数的部分匹配索引CPMI(PMI based on Count),CPMI只选择一部分有价值的查询预先计算并存储,算法步骤(6)至(11)即为筛选有价值查询依据,节点被构建,表示当前查询和对应结果被存储。
CPMI有两个参数N和ε,用来权衡索引的时空耗费,CPMI构建一个索引树,每个节点相当于一个查询q,用x代表此节点,若节点x存储对应查询q的MU(q),则表示节点x是活着的,反之,x死亡,x的孩子节点对应查询q∪{k},k∈[s],k∉q。
在构建CPMI树之前设定三个规则:
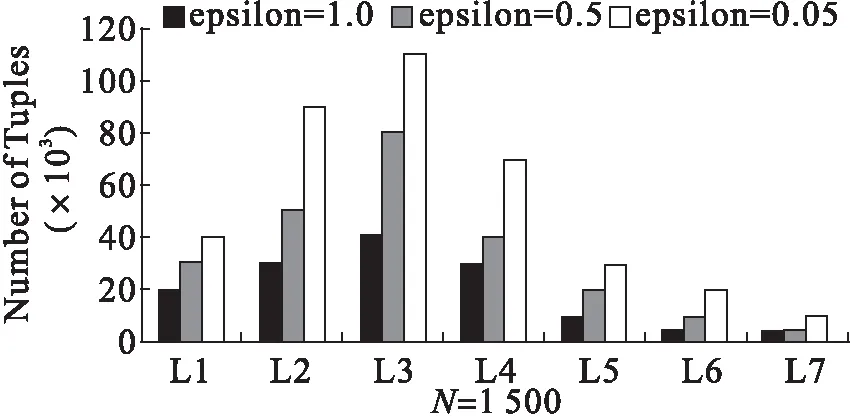
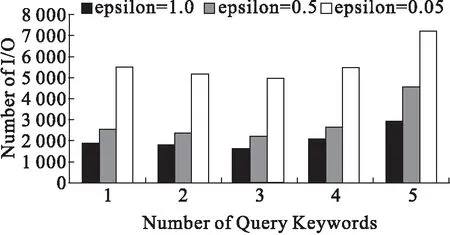
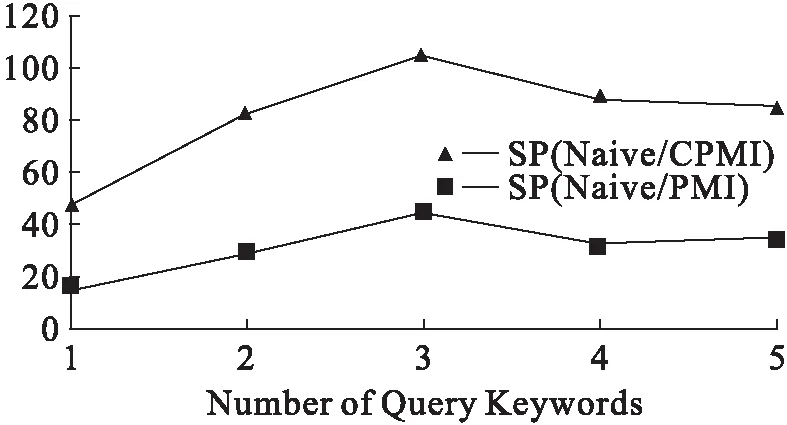
(1)关键词按查询计数排序,形式化描述如下:若有q1={k1},q2={k2},…,qn=(kn)且|MU(q1)|<|MU(q2)|<,…,<|MU(qn)|,则k1 (2)广度优先的方式构建CPMI树; (3)x是将要被构造的节点,输入边标签为k,x′是其活着的父节点,输入边标签k′,若∃k′>k,则节点x不会被构建。 规则(1)保证建立每一级索引花费的时间最短,同时可以令索引拥有较快的检索速度,规则(2)保证了CPMI树与部分匹配索引表的构造顺序,可充分利用每一级索引表,规则(3)保证每个查询q与节点x一一对应,且到达树中某节点的边标签大小是递增顺序,既节省了数据存储空间又避免了很多不必要的计算,缩短了构建时间。下面阐述基于计数的部分匹配索引(CPMI)算法的详细过程。 CPMI算法: 输入:关键词集合{k1,k2,k3,…,kn},数据集U; 输出:CPMI树; 步骤: (1)构建根节点,根节点关联查询q=∅,并存储MU(∅),即U; (2)用关键词集合中的每个关键词分别在U上扫描,得到关键词的查询计数; (3)将关键词集合按照计数排序,并按顺序给每个关键词标号1,2,…,n; (4)树的边关联关键词标号1,2,…,n,对应查询{1}.{2},…,{n}; (5)以广度优先方式构造余下的非根节点; (6)按关键词计数顺序构建第i层节点,i∈(1,2,…),设将要构造的节点为x,x是非根节点,关联某查询q,带有输入边标签为k(k∈q),x′是其父节点,关联查询q′,输入边标签为k′; (7)检测树的第i层是否构建完毕,若构建完毕且第i层有活着节点,则i=i+1,返回步骤(6),若第i层节点全部死亡,则转步骤(12); (8)若k′>k,则节点x不会被构建,返回执行步骤(6),若k′ (9)若x满足条件|MU(q′)|≤N,则x不会被构建且此条件也适用于x所有子孙,x的子孙也都不会被构建,返回执行步骤(6),若|MU(q′)|>N,则执行步骤(10); (10)若x满足条件|MU(q′)|≤(1+ε)|MU(q)|,则x同样不会被构建,但x的某些子孙有可能会被构建,保留节点查询,但不存储MU(q),返回执行步骤(6),若|MU(q′)|>(1+ε)|MU(q)|,则执行步骤(11); (11)构建节点,存储对应MU(q),返回执行步骤(6); (12)CPMI树构建完成。 整体上CPMI算法是依广度优先的方式构造树,步骤(6)依关键词顺序构建,保证查询计数小的关键词都在前面,步骤(8)极大地减少程序计算次数,只有符合条件的查询才会进入到步骤(9)。步骤(9)中条件|MU(q′)|≤N进一步减少了程序计算次数,若将要构建的节点的父节点满足条件则此节点不会被计算。例如Li中查询qi响应结果数小于N,当考虑以qi为父节点而扩展的查询时,直接返回qi的查询结果,因为qi结果精确度已经很高,剔除误报耗费的代价也相当小。步骤(10)中条件|MU(q′)|≤(1+ε)|MU(q)|防止索引大小失衡,既节省存储空间又能保证响应查询q耗费的时间和q的结果数相称。 图3简单展示了由CPMI算法构造的树,图中s=4,输入边标签按顺序依次对应1、2、3、4,虚线节点表示该节点没有被构建,实线节点表示该节点已被构造并存储相应的查询结果到每层节点对应的索引表中,图中节点内的数字表示与节点相对应查询的结果个数,例如图中的100表示|MU(Ø)|=100。可看出,图3中的CPMI树的第k层活着的节点恰好与部分匹配索引表Lk中包含的查询相对应。 图3 CPMI树 每个索引都有与之对应的查询方法,部分匹配索引也不例外。查询基本思想:首先对查询进行预处理,然后在CPMI树上查询得到相应的匹配结果,最终对结果进行提纯再返回给用户。详细流程如下: (2)扫描计数表RTU,对查询q中的关键词按照查询计数排序,得到与q对应的查询标号,q可表示为{1,2,…,m}; (3)依次读取q中关键词标号,自顶向下匹配CPMI树; (4)匹配结束,若未找到与当前查询匹配的节点x转到步骤(6),若找到当前节点x,且x活着,则执行步骤(5),若x死亡,执行步骤(6); (5)得到相应匹配结果,执行步骤(7); (6)回溯:按照原路径返回,直到找到第一个活着的节点xi,对应查询qi,得到响应查询结果MU(qi),执行步骤(7); (7)用余下未匹配的(或已回溯的)关键词提纯查询结果得到提纯后的MU(qi),若MU(qi)≠∅,则执行步骤(8),若MU(qi)=∅,则回溯并得到最近的非空结果集合MU(qj),j (8)返回最终查询结果。 再对CPMI算法进行复杂度分析。根据上文描述的索引构建算法可以得知,本文索引构建基于广度优先算法,在其基础上利用剪枝思想优化CPMI树的构建及存储过程,本文CPMI树来源于Trie树,Trie树在插入方面具有较好的性能,其时间复杂度为O(n),n为关键词个数,而算法的空间复杂度为O(m×n),m为树中活着的节点个数。 在查询时,对于一个查询q需要耗费O(h)找到对应的节点x,h为树的高度,返回的结果集为|Mu(q′)|≤max(N,(1+ε)|MU(q)|),所以时间复杂度为O(h+max(N,(1+ε)|Mu(q′)|))。 我们用实验证明部分匹配索引的实际效果。本文数据集主要由两部分真实数据组成,一部分为结构化数据,另一部分为非结构化数据。结构化数据主要是黑龙江省某年某地区税务数据,非结构化数据主要是搜狐全网新闻数据。本实验主要从索引的构建效率和索引的查询效率两个方面评估基于部分匹配的异构数据索引方法的效果,效率高低主要用索引的构建时间、空间,查询处理的时间来评价。 首先考察索引的构建时间。实验一步骤如下:在数据集相同的情况下,选取构建参数ε=0.05,N在100到10 000之间取值,分别为100、500、1 000、1 500、2 000、3 000、4 000、6 000和10 000,分别记录CPMI方法和PMI方法都建索引耗费的时间。图4展示了两种索引方法时间对比。从图4中可以看出随着的增大索引的构建时间在逐步的减低,这是由索引构建条件(|MU(q′)|>N和|MU(q′)|>(1+ε)|MU(q)|)决定的。图4中CPMI曲线无论在任何时候始终在PMI下方,可见CPMI在构建索引的时间上明显优于PMI。 图4 索引构建时间对比 实验二,参照图4的构建时间,选定N=1 500,令ε的值分别取0.05、0.5和1.0,分别记录构建的CPMI中元组个数。图5展示CPMI中Lk的大小,可以看出ε越小索引Lk中的元组数越多,则索引的命中率越高,查询效率也就越高。 图5 CPMI索引Lk的大小 实验三,接下来验证不同的ε值对索引的查询处理时间的影响情况。据科学统计,在信息检索领域中用户输入关键词的个数为2、3、4的情况占用户查询比例的80%以上。所以本文选取五组关键词,每个查询包含关键词的个数为1~5,对这些查询分别做统计分析。同时本实验采用磁盘I/O来表示查询时间。图6展示了不同ε值对应的查询处理时间,横坐标表示查询关键词个数,可见当ε=0.05时,查询速度最快。 图6 不同epsilon值对应的查询磁盘I/O 实验四,考察已构建索引的查询处理效率。任何索引都是为查询服务的,查询效率是检验索引的重要指标。参照前边实验得出的数据,选取构建索引的参数N=1 500,ε=0.05。此处设定相对加速比(RelativeSpeedUp=Time1/Time2)用以对比各个方法的查询处理时间。实验步骤如下:利用实验三生成的查询关键词组分别在Naive、PMI和CPMI上进行检索,记录每组关键词检索时间并计算其平均检索时间,计算PMI和CPMI的相对于Naive的加速比,具体如图7所示。图7展示了CPMI和PMI同Naive索引方法在处理相同查询时耗费的磁盘I/O数相对加速比。由图7可见CPMI方法同Naive方法的查询时间比值在三个关键词查询时最高(103.17),而PMI则是44.89,即CPMI方法在此时相对节省时间最多证明实验达到了预期的效果。 图7 索引查询时间对比 表1 不同ε的P/R/F 本文仔细分析了异构数据的特点,详细研究了各种现有的数据模型及其对应查询语言,提出了新的数据模型,并构建了与模型相适应的索引及查询机制,提出了一种基于部分匹配的异构数据索引方法,该方法采用以关键词计数为排序标准的索引构建方式并充分利用剪枝思想,较大地减少了构建索引时计算的查询结果数。本文对查询进行预处理,然后在建立的索引上采用分层检索方法,实验证明该方法较大地减少了索引查询时间及构建时空耗费,提高了索引性能。 参考文献(References): [1] BRUGGEMANN R,KOPPATZ P,FUHRMANN F,et al.A matching problem,partial order,and an analysis applying the copeland index[J].2016(22):231-238. [2] DUCH A,LAU G.Partial match queries in relaxed k-d t trees[C]// Proceedings of the Fourteenth Workshop on Analytic Algorithmics and Combinatorics.2017:131-138. [3] 郑霖,徐德华.基于改进TFIDF算法的文本分类研究[J].计算机与现代化,2014(9):6-9+14. [4] LOPEZ-VEYNA J I,SOSA-SOSA V J,LOPEZ-AREVALO I.KESOSD:keyword search over structured data[C].Proceedings of the Third International Workshop on Keyword Search on Structured Data,Scottsdale,AZ,United states,2012.New York:ACM Press:23-31. [5] 王桂玲,韩燕波,张仲妹,等.基于云计算的流数据集成与服务[J].计算机学报,2017,40(1):107-125. [6] LIN W,HU C,LI Y,et al.Virtual dataspace-a service oriented model for scientific big data[C].Proceedings of 4th International Conference on Emerging Intelligent Data and Web Technologies(EIDWT),Xi′an,2013.Washington:IEEE Computer Society:1-5. [7] DIMITRIOU A,THEODORATOS D,SELLIS T.Top-k-size keyword search on tree structured data[J].Information Systems,2015,47:178-193. [8] 张雨佳,苏中滨,吴华瑞.半结构化数据的动态树存储模型研究[J].计算机应用与软件,2011,28(5):86-90. [9] 吴国泉.基于HBase的全文索引及检索技术的研究[D].武汉:华中科技大学,2015. [10]李政,武彤.基于分布式消息队列的企业级全文检索模型研究[J].计算机应用与软件,2017,34(6):292-295+302. [11]杨书新,徐慧琴.基于数据图的关系数据库关键词查询排序研究[J].计算机应用研究,2014,31(2):440-442+447. [12]LOPEZ-VEYNA J I,SOSA-SOSA V J,LOPEZ-AREVALO I.KESOSD:keyword search over structured data[C].Proceedings of the Third International Workshop on Keyword Search on Structured Data,Scottsdale,AZ,United states,2012.New York:ACM Press:23-31. [13]SUBUDHI P,MUKHOPADHYAY S.A novel texture segmentation method based on co-occurrence energy-driven parametric active contour model[J].Signal Image & Video Processing,2017(11):1-8. [14]李先蒙.一种数据空间中非结构化数据查询方法[D].哈尔滨:哈尔滨工程大学,2014. [15]X.DONG,A.HALEVY.A platform for personal information management and integration[C].Proceedings of the 2nd Conf.on Innovative Data Systems Research CIDR,Asilomar,CA,2005.CIDR:l19-130. [16]BLUNSCHI L,DITTRICH J,GIRARD O R,et al.M.A.V.:A dataspace odyssey:the imemex personal dataspace management system(demo[J].Cidr,2013:114-119.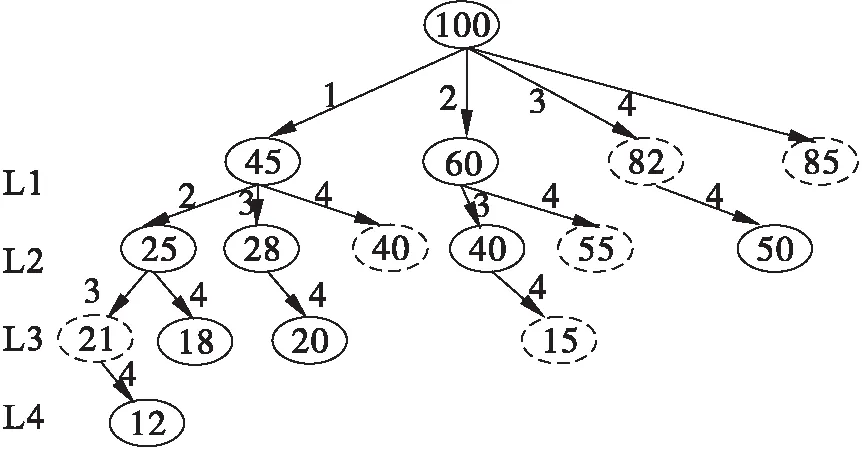
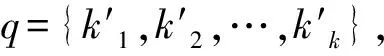
2 实验及结果分析
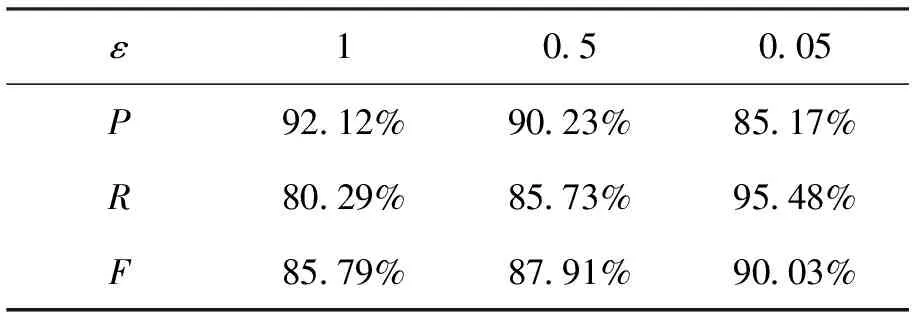
3 结论

