基于组合赋权和改进TOPSIS法的航空发动机性能综合评估研究

周义蛟，郭基联，万 巍，姜禹呈(1.空军工程大学 a.研究生院,b.航空工程学院，西安 710038；.中国人民解放军95959部队，北京 100089)

航空发动机性能评估是精细化、规范化管理使用航空发动机的需要，是确保安全,降低成本，实现视情维修的重要手段。近年来，由于基于多参数航空发动机性能评估方法较以往的基于单参数评估方法具有全面、准确、合理的特点，越来越引起学者和航空公司的重视。目前，航空发动机监控参数众多，各参数反映发动机性能的重要程度无法确切得知，评估中各参数权重的合理确定遇到很大困难。文献[1]采用遗传算法计算各性能参数的权值，然而遗传算法存在一些不足之处，如收敛速度慢，早熟问题等；文献[2]和文献[3]分别采用混沌理论和粗糙集理论进行参数权值的寻优选取，方法新颖，然而对于优化准则函数，需要采集足够多的正常数据和故障数据才能进行合理的寻优控制，从而确定权值，外场保障实际应用较难。文献[4]采用模糊综合评判方法进行发动机状态评估，但并没有考虑各参数指标间的相关性，造成评价信息重复。TOPSIS法是一种常用的多目标决策分析方法，文献[5]～[7]运用了TOPSIS理想解方法进行多目标参数的评估决策，并针对传统TOPSIS法进行相关改进，但文中各参数指标的权重不尽合理。

针对以上问题，本文从外场保障实际应用出发，提出了航空发动机性能综合评估模型，采用组合赋权的方法确定各指标的综合权重，最后基于改进的逼近于理想值的排序方法(Technique for Order Preference by Similarity to Ideal Solution，TOPSIS)进行航空发动机性能综合评估。

1 组合赋权确定综合权重

指标的权重是综合评价的重要信息，合理地确定权重对于评价体系非常重要。层次分析法是主观赋权法中最常用的一种，其能较好地反映评价对象所处的背景条件以及评价者的意图，但权重具有较大的主观随意性;而熵权法是一种常用的客观赋权法，通过实际的原始数据来确定权重，但其可能会造成重要指标的权重反而较小的不合理情形。为此本文引入纳什均衡思想将上述二者融合起来，得到主客观意义上的综合权重，从而使求得的权重更加科学合理[5]。

假设航空发动机综合性能评估指标采用α种方法对β个评价指标进行权重计算，那么可定义采用第λ中评价方法求出的权重为

Wλ=(ωλ1,ωλ2,…,ωλβ)λ=1,2,…,α

(1)

综合权重的线性组合为

(2)

其中，φλ为待求参数，根据组合赋权集结模型予以求解。

组合赋权确定综合权重，其基本思想是融合主客观权重，基于均衡的思想，在所建立的不同的权重之间，使得所得的综合权重跟各个基本权重之间的各自偏差极小化，从而获得更加科学的结果。因此，对式(2)而言，就是综合权重线性组合系数φλ的优化过程，使得W与各个Wλ的偏差极小化。因此，基于组合赋权求解综合权重的模型如下

(3)

由式(3)可知，本模型利用矩阵的2范数，对多个目标函数进行优化，获得均衡可靠的综合权重值。

根据矩阵论中的矩阵微分思想，式(3)的最优化一阶导数条件为

(4)

2 传统TOPSIS法改进

研究传统的TOPSIS方法不难发现，传统的TOPSIS方法存在逆序和中垂线矛盾问题，并且其计算的各指标与正、负理想解的欧氏距离没有考虑到决策指标之间的相关性以及指标所占权重不同的影响。本文借鉴文献[6]中基于TOSPSIS法的改进思路，提出改进方法。

(1)针对逆序问题，其本质是因为正、负理想解位置发生改变。因此，为消除逆序带来的影响，假设发动机有n个性能参数的指标，本文根据外场发动机监控数据以及发动机手册，确定各性能参数的绝对正、负理想解。

(2)针对中垂线矛盾问题，本文首先按照TOPSIS方法进行评估，然后判断两两评价对象是否位于同一垂线，若位于同一垂线，按照外场监控的单参数性能排队指标排气温度裕度(Exhaust temperature margin,EGTM)进行排序，并替代原来的排序结果[7]。

(3)针对性能参数之间的相关性问题，本文将采用马氏距离代替欧式距离，引入协方差矩阵对传统的TOPSIS方法进行改进[8]。

3 基于改进TOPSIS法与组合赋权的航空发动机性能综合评估模型

本文融合改进TOPSIS法以及基于组合赋权的综合权重理论，构建了一个合理可靠的航空发动机性能综合评估模型，其步骤如下:

步骤1：针对航空发动机综合性能评估指标体系的层次结构模型各指标的特性，确定评价指标矩阵X=(xij)m×n；

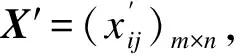
(5)

步骤3：基于组合赋权确定综合性能评估指标的综合权重W={w1,w2,…,wj}；

步骤4：结合步骤3计算出的综合权重值，建立加权后的规范化评价指标矩阵Y=(yij)m×n。其中

(6)

步骤5：确定航空发动机各评价指标的绝对正、负理想解Z+和Z-。由于航空发动机性能参数可分为效益型指标、成本型指标，因此，定义如下绝对正、负理想解

Z+={(maxzij,j∈J1),(minzij,j∈J2)}

(7)

Z-={(minzij,j∈J1),(maxzij,j∈J2)}

(8)

其中，式(7)和(8)中J1为评价指标中效益型指标的集合，即取值越大越好；J2为评价指标中成本型指标的集合，即取值越小越好；

步骤6：采用马氏距离计算评价指标到绝对正、负理想解的距离[9-11]

(9)

(10)

步骤7：计算各评价对象的相对贴进程度A，作为发动机综合性能评估值，为外场单台发动机性能监控、维修保障及多台性能排队、预测下发提供依据。

(11)

4 实例分析

根据航空发动机监控指标以及外场使用保障相关方法，以CF34-8C5B1发动机为例，构建航空发动机性能综合评估指标体系，如图1所示[12-15]。

图1 航空发动机综合性能评估指标体系

图1中气路参数的偏差值是指在使用过程中的发动机参数与健康发动机性能基线值相比较而获得的。由于航空发动机是在多工况条件下工作的，即受外界影响很大，例如大气温度、湿度、海拔高度等因素。为准确、合理地进行发动机性能评估，必须进行参数的标准化，消除外界复杂工况影响，因此本文选取气路性能参数的偏差值作为综合性能评估的部分指标。

(1)通过分析CF34-8C5B1发动机监测数据以及发动机手册，确定相关指标绝对正、负理想解，如表1所示。

表1中，对于燃油流量偏差值(Fuel flow deviation value,DFF)的负理想解和滑油温度(Lubricating Oil Temperature， OILT)的正理想解，发动机手册并未给出详细数据，因此本文采用拉依达准则，通过分析近两年来10台同型号发动机的监测数据，计算燃油流量偏差值以及滑油温度的均值和标准差，从而确定其结果，如表1所示。

(2)选取某年10月份以来10台同型号的发动机性能参数值，如表2所示。

(3)首先对原始数据进行归一化处理，得到发动机各评价指标的处理后的矩阵X′。通过熵权法求得发动机各指标参数的客观权重为W1={0.1260,0.1404,0.0702,0.1104,0.1229,0.1469, 0.1450,0.1382}，然后通过层次分析法确定各指标参数的主观权重W2={0.1660,0.3377,0.2651, 0.0224,0.0315,0.0291,0.0459,0.1023}。然后基于纳什均衡思想，由式(4)计算可得，φ1=0.28，φ2=0.72。最后通过式(2)计算航空发动机各参数指标的综合权重计算，结果如表3所示。

表1 CF34-8C5B1发动机相关评价指标绝对正、负理想解

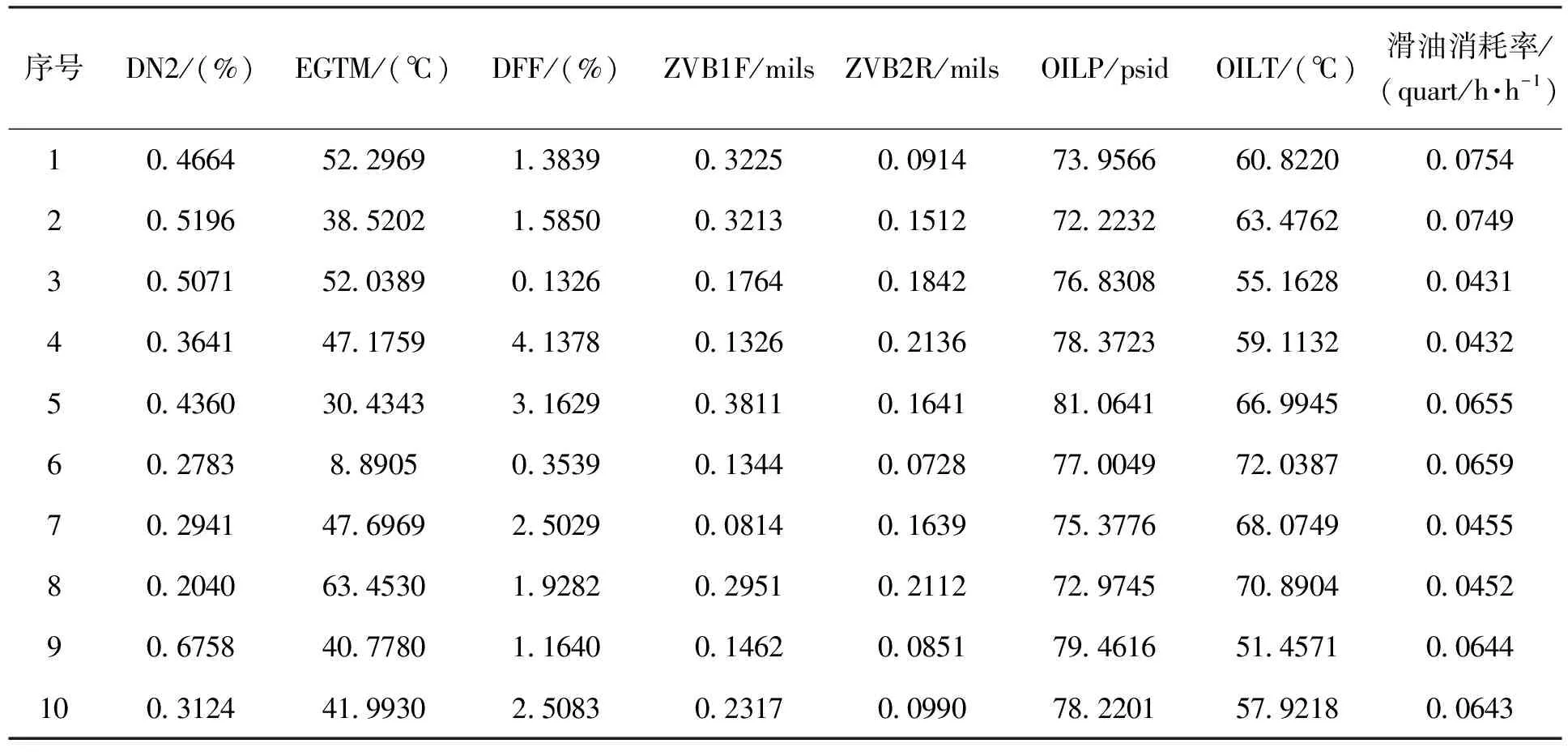
表2 CF34-8C5B1发动机参数值

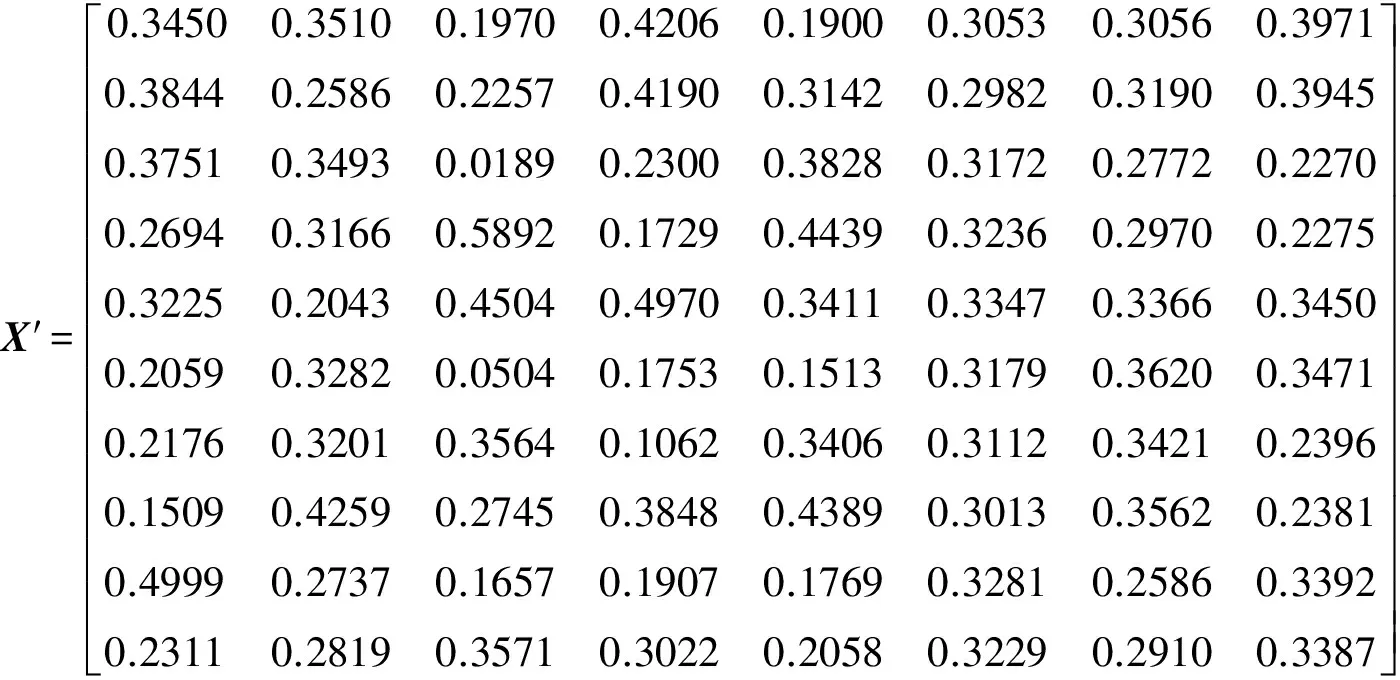
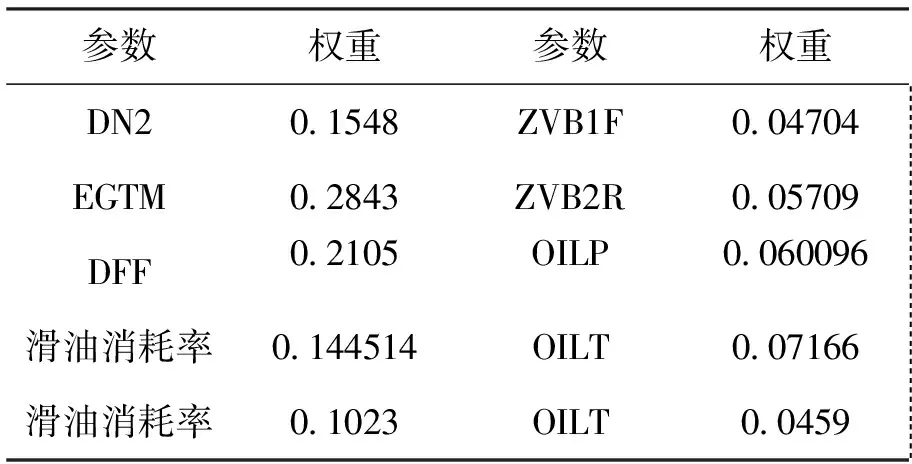
表3 CF34-8C5B1发动机性能评价指标综合权重

(4)结合上述步骤，计算出航空发动机综合评估结果，如图2所示，并将航空公司常用排气温度裕度EGTM进行发动机性能排队方法与本文所提出的发动机性能综合评估值进行对比，结果如表4所示。

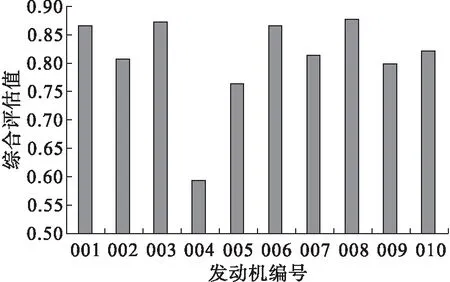
图2 航空发动机综合性能评估值

将表4中综合性能评估值排序和EGTM排序值对比发现，排序结果大体一致。相差较大的有编号为004的发动机。通过实际发现。编号为004的发动机燃油流量较大，在外场已被列入异常监控项。编号005发动机使用时间最长，性能具有一定衰退，综合评估值和EGTM排序结果基本符合。因此，综合性能评估相比于EGTM排队，更为准确合理，在发动机性能排队，制定维修决策上，具有一定的借鉴意义。

(5)计算判断矩(Xi-Xj)(Z+-Z-)是否为零，从而确定两两发动机性能参数值是否在同一中垂线，其中Xi和Xj为两台发动机参数向量，Z+和Z-表示绝对正、负理想解。经计算，不存在位于同一中垂线上的点，发动机性能排队结果不变。

(6)利用综合性能评估值，对编号005的发动机进行性能趋势分析，如图3所示。

可以看出，近10个月来，随着循环小时的增加，航空发动机综合性能具有一定的衰退，并根据外场实际情况，发动机运行一段时间后，外场将会采取一定措施进行性能恢复。因此进行实时综合性能趋势监测，在外场实际保障维护工作中，能为预防故障、制定维修计划提供借鉴。

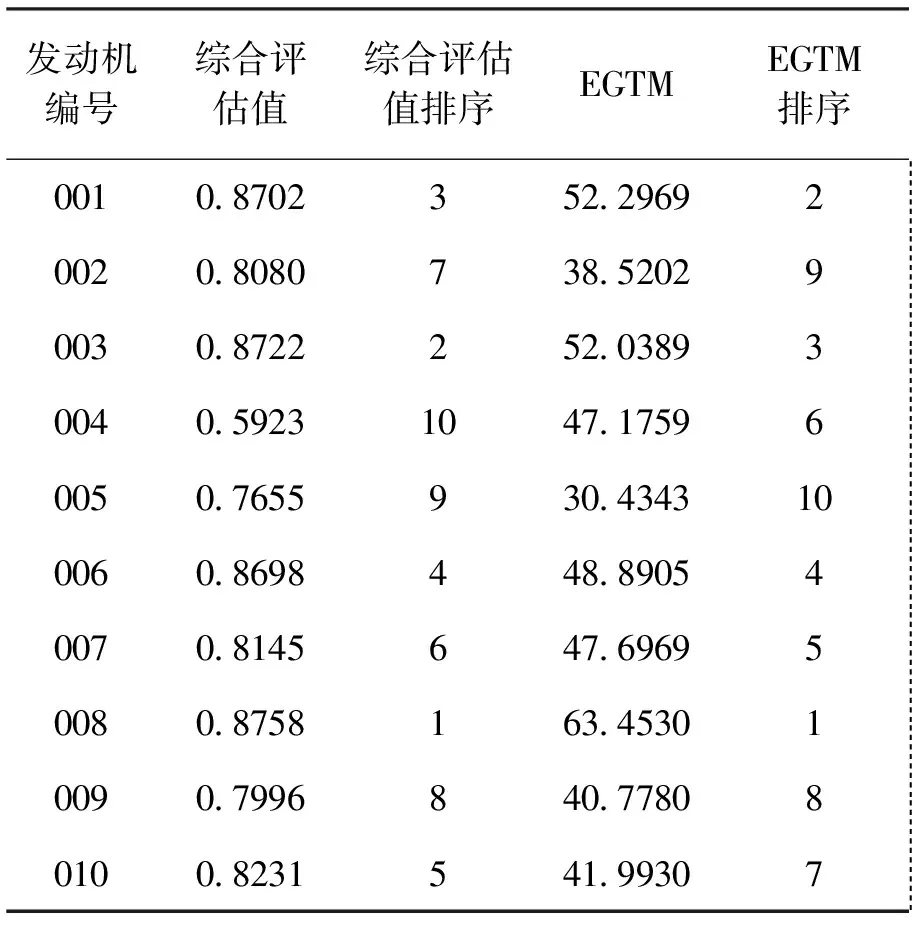
表4 CF34-8C5B1发动机性能评估结果

图3 综合性能趋势图

综上所述，无论是多台发动机的性能排队，还是单台发动机的性能趋势预测，文中所提方法都符合外场发动机综合性能监控实际，验证了该方法的有效性，具有很好的工程应用价值。

5 结论

本文基于外场保障实际，构建了基于改进TOPSIS法和组合赋权航空发动机性能评估模型。采用组合赋权确定综合权重，既可克服客观权重的片面性，又可避免主观权重的随意性。引入改进TOPSIS法进行航空发动机综合性能评估，并通过工程实例验证了该方法的合理性。研究发现，航空发动机性能综合评估相比于EGTM排队，在外场监管、使用、维护发动机方面，无论是单台发动机的性能趋势预测，还是多台发动机的性能排队，都更为准确、合理，具有重要的实际意义和参考价值。

参考文献(References)：

[1] 胡金海,谢寿生.基于遗传算法的发动机性能监控与故障诊断[J].推进技术,2003,24(3):198-200.

[2] 侯胜利,胡金海,李应红.基于混沌变量的航空发动机性能监控与故障诊断[J].航空动力学报2005,20(2):314-317.

[3] 胡金海,谢寿生,胡剑锋,等.基于粗糙集理论的航空发动机性能综合评判[J].系统工程与电子技术2006,28(5):704-707.

[4] 王梦琦,王瑞民,杨雪.基于改进模糊综合评判的航空发动机状态评估[J].润滑与密封,2011,36(1):80-84.

[5] 黄晓燕.基于改进TOPSIS法的航空发动机性能评估方法[J].制造业自动化,2014(8):73-77.

[6] 齐晓骥.基于多参数的发动机综合性能评估[D].天津:中国民航大学,2016.

[7] 王正新.基于马氏距离的TOPSIS决策方法及其应用[J].经济数学,2012,29(2):17-20.

[8] COSTA T F G,LOHMANN G,OLIVEIRA A V M.A model to identify airport hubs and their importance to tourism in brazil [J].Research in transportation Economics,2010(26):3-11.

[9] DUVAL D T.Critical issues in air transport and tourism[J].Tourism Geographies,2013,15(3):494-510.

[10]FORSYTH P.Tourism benefits and aviation policy[J].Journal of Air Transport Management,2006,12(1):3-13.

[11]曹惠玲.基于AHP及灰色关联分析法的发动机健康评估研究[J].数学的实践与认识,2015,45(2):122-128.

[12]于文武,许春生,康力平.基于AHP的航空发动机健康评估系统设计[J].航空计算技术,2007,37(1):73-76.

[13]ROBERTO R M.Tourism service quality begins at the airport [J].Tourism Management,2006,27(5):874-877.

[14]DWYER L,FORSYTH P,SPURR R,et al.Economic impacts of a carbon tax on the australian tourism industry [J]Journal of Travel Research,2013,52(2):143-155.

[15]谢晓龙.航空发动机性能评价与衰退预测方法研究[D].哈尔滨：哈尔滨工业大学，2016.