股灾背景下沪深股市波动率的结构转换特征分析
罗 君,乔高秀,王 璐
(1.西南财经大学 统计学院,成都 611130;2.西南交通大学 数学学院,成都 611756)
0 引言
2015年,我国沪深两市单日成交额不断刷新,各项指数不断攀高,在6月创出历史最高点5178;然而随后两个多月内,千股跌停的事件重复上演,累计跌幅高达45%。机构投资者、散户和专家学者见证了我国股市跌宕起伏、风雨交加的形势,从“疯牛”到“股灾”的演变过程。
研究发现,重大的政治和经济变革、技术创新、金融风暴、新政策的出台等因素都将引起股市收益率波动结构发生显著变化。随着全球金融市场波动加剧,很多学者试图找到合适的模型来刻画波动率的结构转换特征。Hamilton(1994)[1]首次将马尔科夫结构转换机制与ARCH模型结合,建立了具有马尔可夫结构转换机制的ARCH模型,被广泛地应用于金融时间序列的波动率结构变化分析。Klaassen(2002)[2]对状态转移GARCH模型进行改进,利用前一时刻的条件均值代替当前时刻的方差,给出了波动率多步向前预测的显示表达。Marcucci(2005)[3]利用MRSGARCH模型分析预测美国标准普尔100指数(S&P100),发现在均方误差作为准则的统计损失函数标准下,MRS-GARCH模型比标准GARCH模型能更精确地预测股市波动。国内学者对沪深股市波动率的结构特征也进行了不少实证研究[4,5]。
本文在已有研究的基础上,采用Klaassen(2002)[2]的MRS-GARCH模型研究2015年沪深股市波动率结构转换特征的异常行为。为了比较股灾发生时股市波动率的异常行为,本文进一步给出了基于2005—2015年样本的实证结果,并对MRS-GARCH模型的预测效果进行评价分析。
1 MRS-GARCH模型
1.1 模型介绍
状态转移模型本质是根据波动变化特征选择不同的状态变量,使之可确切地刻画不同状态的真实现状。状态变量st在不同状态间转变遵循马尔科夫过程。其一阶转换概率为:

其中,pij表示由t-1时刻状态i转换到t时刻状态 j的概率。通常说来,两个状态的马尔科夫链状态转移矩阵形式为:

一般情况下,MRS-GARCH模型为:

其中,f(.)表示可能的条件分布,包括正态分布(N)、学生分布(T)及广义误差分布(GED);θt(i)表示状态i下不同分布特征的参数集合;p1't=Pr[st=1|ζt-1]表示t时刻处于状态1的概率,其ζt-1涵盖了t时刻前观察到的所有方差信息。
确切地讲,时变的参数被分解为三部分,满足下列等式:

其中表示条件均值表示条件方差,νt(i)表示条件分布的参数。
MRS-GARCH模型包含了四个部分:条件均值、条件方差、状态转移机制和条件分布。从MRS-GARCH模型结构分析可知,求解rt的密度函数等价于求解条件均值、条件方差和时变条件分布的各个参数。rt的条件均值方程是一个随机游走过程(可能存在截距项),条件方差方程是根据整个状态路径(包括未观测到的路径),其表达形式如式(4)和式(5):

其中,i=1'2,νt是一个零均值,方差为1的随机变量。

与GARCH(1,1)模型条件方差方程类似,MRS-GARCH模型条件方差表示为:

其中,ht-1代表无状态依赖历史条件方差。
为了规避方差依赖于过往时期的全部状态路径,同时便于实现多步向前预测,Klaassen(2002)[2]在Gray(1996)[6]的方法上进行改进,基于t-1时刻的条件均值代替条件方差,其表达形式为:
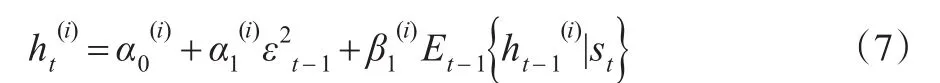
其中,t-1时刻条件均值计算为:
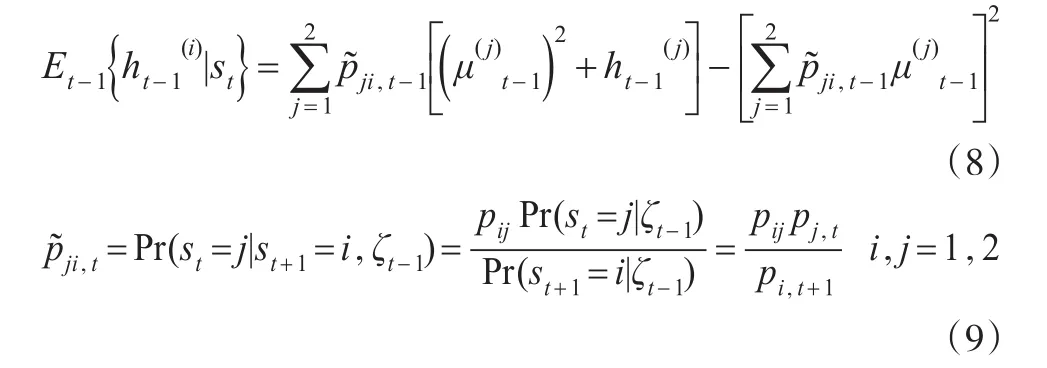
在捕捉股市收益率处于不同状态下的特征和转换机制时,通常使用两种状态(高/低波动)的MRS-GARCH(1,1)模型:

1.2 参数估计
研究表明,马尔科夫状态转移模型的参数估计可以采用极大似然估计方法,但最关键的问题是能刻画出先验概率 p1't=Pr(St=1|ζt-1),即根据t-1时刻前的信息计算t时刻处于状态1时的概率值。其一般表达式为:
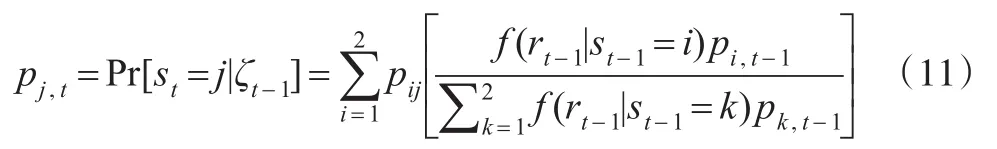
其中,pij表示t-1时刻处于状态i到t时刻处于状态j的转换概率。对数似然函数如下:

其中 f(.|st=i)表示t时刻处于状态i时的条件分布函数。
1.3 模型预测
Klaassen(2002)[2]的MRS-GARCH模型与其他MRSGARCH模型相比有一个显著的优点,即给出了多步向前波动预测的显示表达,其计算公式是基于标准GARCH模型结构通过递推的方式得到。以T时刻为预测原点,m步向前的波动预测的计算式:
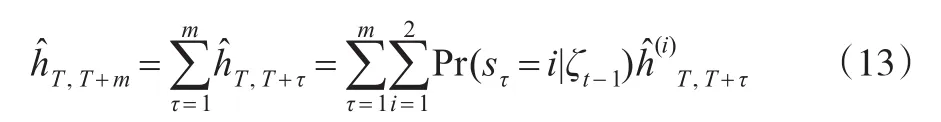
其中,表示T时刻起向前m步的方差预测之和,ĥ(i)
T'T+τ表示时刻T处于状态i向前τ步的方差预测值,可以通过递推的方式计算:

可见,多步向前的波动预测值可以通过对各个状态下多步向前方差预测值的加权平均计算而得,其中,权重是由预测概率决定。通常情况下,计算方差预测值会采用滤波概率。其中,间隔为τ时的滤波概率为:

2 实证分析
2.1 样本选取与描述性分析
沪深300指数作为反映A股市场整体走势的一个重要指标,具有较好的市场知名度和较高的市场覆盖率,能真实全面地反映市场股市的价格动态演变。因此,本文以沪深300指数日收盘价为样本来研究沪深股市波动率的结构转换特征,2015年全年的样本量为237,数据来源于雅虎财经数据信息平台。
图1给出了沪深300指数在2015年的日收盘价和收益率。可以看出,沪深300指数收益率波动具有明显的聚集性、突发性、时变性等特征,股市在6月达到最高点,8月跌至最低点。

图1 2015年沪深300指数收盘价和收益率
对沪深300指数收益率的描述性统计分析见表1。可以看到,沪深300指数收益率的峰度明显高于标准正态分布峰度值3,且偏度小于0,则分布呈现左偏趋势,样本的峰度值和偏度值说明了分布呈现明显的尖峰肥尾特征;JB统计量的值可以进一步论证收益率序列不服从正态分布;LM统计量的相伴概率 p值均小于给定的显著性水平值0.01,表明收益率序列具有高阶ARCH效应,因此本文可以利用条件异方差模型来拟合收益率的波动性。

表1 沪深300指数收益率描述性统计量
2.2 MRS-GARCH模型估计结果
本文为简化参数估计,选取一阶的状态转移模型,并假设模型的残差项分别服从正态分布(N)、学生分布(T)、广义误差分布(GED),且认为学生分布自由度也会随着状态的变化而改变,用T1和T2表示低、高低状态下的不同自由度。表2给出了通过极大似然估计方法得到的MRS-GARCH模型参数估计结果,其中,状态1、状态2分别表示股市处于低、高波动状态,其中,p表示从状态1演变到状态1的概率,q表示从状态2演变到状态2的概率;ρi=α1(i)+β1(i)(i=1'2)反映高、低状态下波动率的持续性。
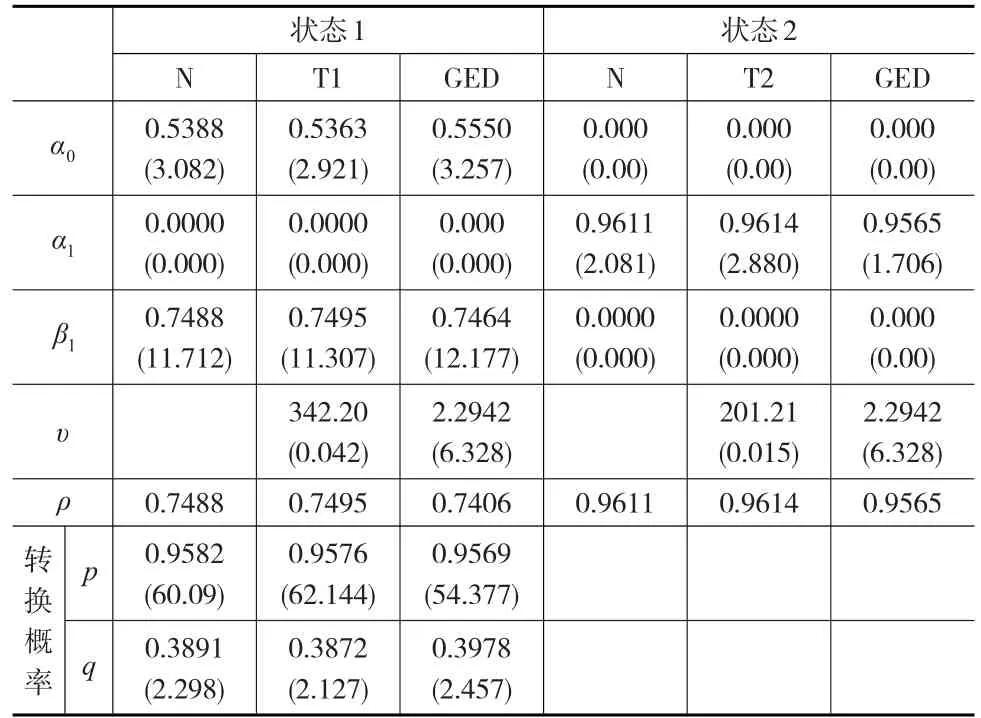
表2 MRS-GARCH模型参数估计结果(2015年)
由表2可以看出,在低、高波动状态下,参数间存在着显著的差异,说明沪深300指数收益率的波动存在明显的高、低波动两种状态,且波动在不同状态之间的行为也存在较大差异。在低波动状态,影响当前期波动的主要因素是前一期波动信息,而在高波动状态,影响当前期波动的因素主要是前一期的残差扰动项。从波动的持续性ρi(i=1'2)结果显示,沪深300指数波动处于低波动状态持续性大致为0.75,处于高波动状态持续性在0.96左右,表明2015年沪深300指数处于高波动状态的持续性明显强于处于低波动状态的持续性。从转移概率值可以发现,从低波动状态向低波动状态转移概率值超过0.96,从高波动状态向高波动状态转移概率值仅是0.39左右。从高、低两状态转化分析,波动状态从高向低演变的可能性(0.61)明显大于从低向高演变(0.05),表明2015年沪深300指数收益率波动更倾向于从高状态转移到低状态。
由于扰动项分布不同时MRS-GARCH模型估计先验概率和两状态波动率相差不大,图2给出了MRS-GARCH-N模型处于高波动状态时先验概率、以及在高、低状态下的方差。若先验概率值越大,沪深股市处于高波动状态的可能性越大。图2显示在2015年第二季度末至第三季度,处于高波动状态的概率值随着时间变化高低起伏,且高波动状态方差明显高于低波动状态方差,表明股市波动剧烈。这正与2015年我国股市的实际状况吻合,股市在6月飙升至最高点,随后开始断崖式的跌落。

图2 MRS-GARCH-N模型先验概率概率和方差(2015年)
2.3 比较分析
为了与股灾发生时沪深股市波动率的结构转换特征作比较,本文进一步选取2005年4月8日至2015年12月18日沪深300指数日收盘价数据作为样本得到参数估计结果,见表3。

表3 MRS-GARCH模型参数估计结果(2005—2015年)
由表3可知,沪深300指数收益率的波动存在明显的高、低波动状态。波动的持续性ρi(i=1'2)的值均大于0.89,说明沪深300指数波动处于高、低状态的持续性均较强;但也存在细微的差异,例如在MRS-GARCH-GED模型中,股市在低波动状态的持续性强于高波动状态。从转移概率 p和q可知,沪深300指数波动更易在同类状态间转换,即从高波动状态向低波动状态演变或者从低波动状态向高状态波动演变的概率值均较小。
下页图3给出了MRS-GARCH-GED模型处于状态2的先验概率和两状态下的方差,其中黑实线表示状态1下的方差,灰虚线表示状态2下的方差。
从图3可知,自从2005年开始实施股权分置政策以后,到2006年部分非流通股上市,股市波动开始逐步增强,2007年进入了高波动状态。这可能是由于市场中股票流通量的增加以及次贷危机的影响,沪深股市在双重因素的影响下从制高点往下跌,并一直处于高波动状态,直至2008年美国的次贷危机演绎成全球金融危机,经济增速缓慢,股市持续下跌,波动较低。2009年国家放松财政和货币政策,确立以“调结构、促销费”经济发展理念及市场自身调节能力,上市公司并购重组活跃,股市开始反弹上涨并处于高波动状态;沪深股市波动经历了2008年、2009年的大起大落,伴随着中央宏观经济调控及时有效地实施,股市开始扭转趋势并在随后几年里保持平缓的趋势,股市波动处于低状态;2015年股市跌倒起伏,从2015年6月12日的最高点开始出现断崖式下跌。一方面是由于中国处于经济转型期,监管出现漏洞,导致短期炒作、迅速套利现象显著,另一方面是市场“融资”“融金”“配资”规模快速发展,引发股价快速持续上涨孕育了“泡沫式”的股票市场,因此导致2015年股市剧烈波动。
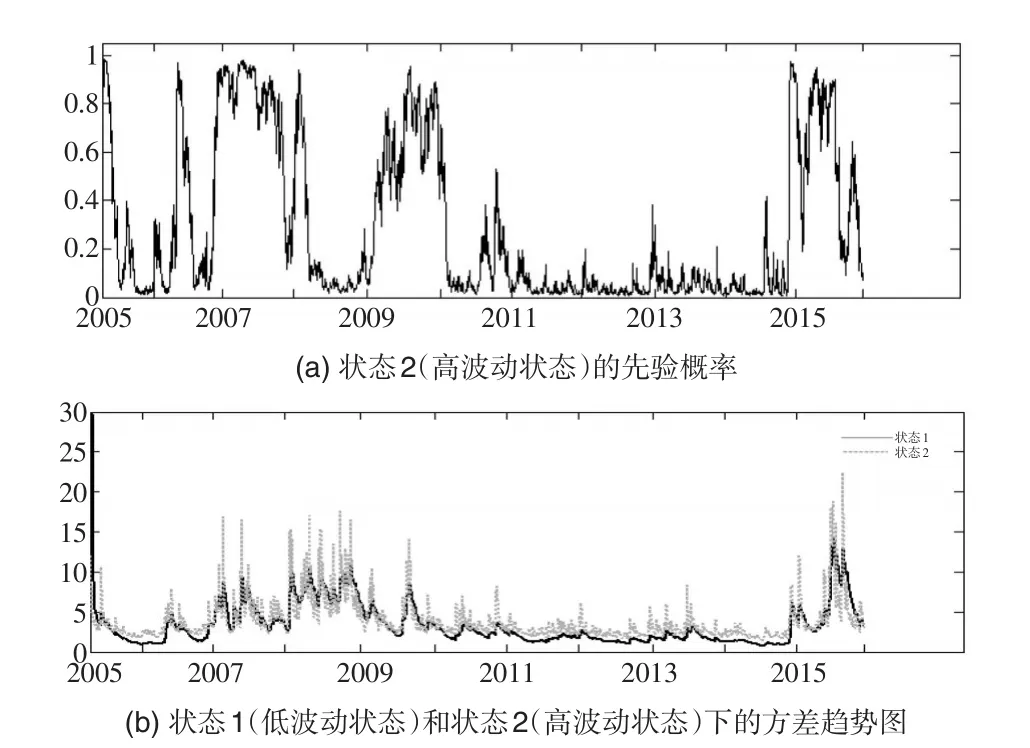
图3 MRS-GARCH-GED模型先验概率和方差(2005—2015)
2.4 模型评价
本文采用四个常见的统计量作为评价准则,包括AIC值、BIC值、对数似然函数(LOG(l))及均方误差(MSE),对各个模型估计结果及样本内的预测能力进行评价。其中:是隐含的真实波动率,是波动率的预测值。利用Marcucci制作的程序包,以对数收益率的平方近似隐含的真实波动率,通过一步窗口滚动方法,做向前一步的样本内预测。结果见表4。
由表4可知,综合各项评价指标表明状态转移模型的拟合效果和样本内的预测能力优于标准GARCH模型,认为我国沪深股市波动存在着明显的高、低状态间转换行为。2015年股灾发生时MRS-GARCH-N模型拟合效果最佳,而在2005—2015年此阶段发现MRS-GARCH-GED模型具有更好的拟合效果。
3 结论
本文采用Klaassen(2002)[2]的MRS-GARCH模型研究我国股市波动率的结构转换特征,特别是2015年股市动荡期间的表现。结果显示,沪深股市存在显著的波动聚集性、持续性,这与国外高度成熟的证券市场股市波动结论相似,表明我国股票市场经过十几年的发展逐步趋向成熟。同时,沪深股市存在明显的高、低波动,且波动在不同状态的行为存在差异性。

表4 各模型评价结果
沪深股市波动存在着高、低状态间转换行为。2005—2015年的全样本实证结果得知沪深300指数波动更易在同类状态间转换,即从高波动状态向高波动状态演变或者从低波动状态向低状态波动演变的概率值均较大;然而在2015年股灾背景下,沪深股市更易于从高波动状态向低波动状态演变(p在0.95附近,但q在0.38附近),表明了2015年沪深股市波动的异常行为。
在股灾背景下,沪深股市波动处于高状态(ρ2在0.96左右)持续性强于低状态(ρ1在0.74左右);而全样本拟合结果显示股市处于低、高状态的持续性均较强,但股市处于低波动状态的持续性略强于高波动状态(ρ1=0.997'ρ2=0.925)。因此,进一步说明2015年沪深股市处于高波动状态的持续性大于整个样本阶段处于高波动状态的持续性。
[1]Hamilton J D.Time Series Analysis[M].Princeton:Princeton University Press,1994.
[2]Klaassen F.Improving GARCH Volatility ForecastsWith Regime-Switching GARCH[J].Empirical Economics,2002,27(2).
[3]Marcucci J.Forecasting Stock Market Volatility With Regime-Switching GARCH Models[J].Studies in Nonlinear Dynamics&Econometrics,2005,9(4).
[4]刘家鹏,苏涛.中国股市非对称性收益的实证研究[J].统计与决策,2010,(3).
[5]赵健.不同分布下中国股市波动性解析[J].统计与决策,2014,(16).
[6]Gray S.Modeling the Conditional Distribution of Interest Rates as a Regime Switching Process[J].Journal of Financial Economics,1966,42(1).

