例谈物理验证中舍解的依据与意义

李桂旺

(江苏省前黄高级中学，江苏 常州 213161)

随着科学技术的发展,要求培养出善于创新的复合型人才,这就要求教师对学生进行物理科学素质及学科渗透能力的培养．应用数学处理物理问题的能力是物理学科的关键能力要求,也是分析与解决问题的重要手段之一．

数学是解决物理问题的重要工具,在利用数学工具解决问题中我们常常要求对分析的结论进行验证,以确定结论的科学性与合理性．数学的多解也是物理问题中比较常见的情形,但数学的多解不一定有物理意义或都合理,如何排除不合理的数学解是平时教学过程中需要关注．也就是对最后形成的结论进行论证,没有物理意义的“解”需要舍去,从而排除这种“物理不可能”,使结论更具科学性．

1 规律的持续性

物理情景中,事件的发展的过程所遵循的规律有时并不单一．由于物理过程所遵循规律的变化从而致使部分“结论”无“意义”,此解应当舍去．同时也需要研究变化后的新规律对应的结论．

例1.一辆汽车沿水平路面以速度108km/h正常行驶．司机由于特殊原因进行急刹车(不考虑反应时间),则刹车后汽车前进72m需要多长时间?(已知汽车与与水平路面的摩擦因数为μ=0.6,g=10m/s2)

解析:对匀变速运动规律应用比较熟悉的同学,遇到这种类型的问题应对相对轻松．但对刚学习这部分内容的学生,通常是按部就班利用匀变速直线运动规律来分析解决问题．

其中v0=108km/h=30m/s,a=μg=-6m/s2，即

得t1=4s或t2=6s(舍去).

舍解的依据:此情涉及到交通工具刹车类问题,应用规律时是简单套用匀变速直线运动规律．实际模型是，汽车刹车后仅需要t0=v0/a=5s时间停止,故t2=6s的解应该舍去．此类问题习惯称为“交通工具刹车类”问题．

被舍解的意义:实际上直接运用匀变速运动规律是误以为汽车刹车后一直匀变速直线运动,即全程加速度一直不变化的运动,此解为“返程”时到达72m处时的时间．通过判断发现,汽车停止后就不会再回头加速运动．

2 时间的方向性

在匀变速直线运动中物体(质点)的位移是时间的二次函数,当涉及到时间时,一般是两解．此时就需要验证两解是否都有意义．

例2.已知某住宅楼三楼空调外机安装平台高6米．某工人在该平台以初速度5.0m/s竖直向上抛出一个物体(抛出时手伸在平台外侧,下方是安全区域)．则需要多长时间物体可到达抛出点下方3.75m处?(不考虑阻力且重力加速度g=10m/s2)

解析:本题是竖直上抛运动规律的应用．直接利用匀变速直线运动规律．取向上为正方向

得t1=1.5s和t2=-0.5s(舍去).

舍解的依据:因为时间的变化是有方向性的,物体是沿时间变化的方向发生位置变化的．而联立方程时取抛出点为计时0时刻,即此后的时刻才符合要求．

被舍解的意义:从物理角度看时间“负”值,其物理意义应该表示“过去”,即t2表示抛出之前的0.5s时．之所以数学上有解,是因为方程只能呈现位移与时间的关系无法体现时间发展的方向性．即可将这个物体的运动曾经(-0.5s时)出现在该位置,中途(0时刻)经过了抛出点后再经过1.5s时通过该位置．

3 潜在条件约束

在事物发展变化过程中原本就会可能出现多解的情况,因特定条件下约束从而舍解．这类条件有可能是显性的也可能是隐性的,解析过程中要将其转化为数学条件而限制．

例3.已知某住宅楼三楼空调外机安装平台高6m．某工人在该平台以初速度5.0m/s竖直向上抛出一个物体(抛出时手伸在平台外侧,下方是安全区域)．则需要多长时间物体距离平台3.75m?(不考虑阻力且重力加速度g=10m/s2)

解析:粗看上去这题与例2似乎相同,仔细审题发现区别在问题上．在例1中明确指出物体在抛出点下方的位置,而本题中没有这个要求,自然需要考虑上方的情况．

与例2同理．取向上为正方向有方程

因为Δ<0，所以没有数学解．

舍解的依据:通过条件约束判断发现,物体上升的最高点H=1.25m,不可能出现在上方3.75m处．

被舍解的意义:此讨论的“解”是一种分析过程,审题过程中是需要考虑到这种情型存在的可能性．只能通过定量分析通过数学解去否定了这种情型．如果试确定距离抛出点1m处需要的时间,上方的情型“解”就物理意义．

图1

进阶:如图1所示,现有一单面长度为24m的水平传送带,以22m/s速度逆时针匀速运转．在传送带左端一小物体(可以看着质点)以20m/s初速度向右滑行,物体与传送带间的摩擦因数为0.8．则物体发生位移20m需要多长时间?(

g

=10m/s

2

)

解析:若单纯看这个问题其实就是匀变速直线运动规律的应用,若结合“例1”来看,似乎是“交通工具刹车类问题”．但由于传送带不是静止而是速度反向且大于物体初速度,故物体先做匀减速直线运动,后返回做匀加速直线运动(若传送带足够长),且加速度不变,即遵循匀变速直线运动．

取向右为正方

其中

v0=20m/s,a=μg=-8m/s2，

则

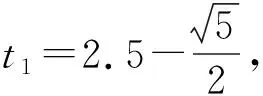
舍解的依据:表面看两解都大于0,没有出现“例2”中的“时间方向”性的问题,也没有出现“例1”中“交通工具刹车”情况而停止．但没有考虑“传送带长度”的“潜在约束”．通过判断发现,物体向右前进25m时速度为0,已超出传送带长度而“离开”传送带．故t2不符合实际情况．

被舍解的意义:在分析中没有注意到“传送带”实际长度的“约束性”,t2解实际是反应传送带足够长的情况下,物体再此返回到20m位置时的情型．

4 能效的合理性

物理模型的建立首先符合数学规律,但符合数学规律的不一定有物理意义,或者即便有物理意义,但“性价比”(效率等)较低.理论上可以存在，但不利于采用,此时的“解”要舍去．

例4.如图2所示,一电动机用电动势为100V的电源供电,电源内阻为r=1Ω,电动机的线圈内阻为R=4Ω,正常工作时电机输出机械功率为180W．试确定此时电路中电流是多少?

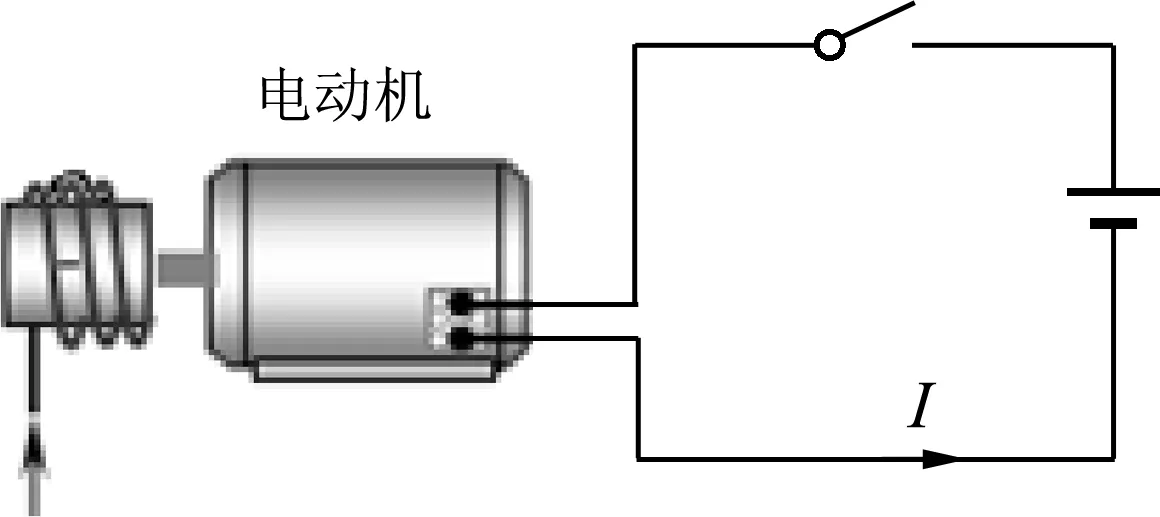
图2

解析:本题只是闭合电路欧姆定律的应用问题,由题意不难得到如下关系．

P机=EI-I2(R+r)，

即180=100I-I2(1+4)，

有I1=2A或I2=18A(舍去).

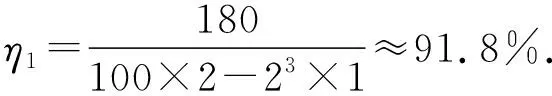
被舍解的意义:I2=18A时,在数学上是有意义的．理论上符合这种数学解的电机是都可以生产出来的,只是两种(2A与18A)电机制造工艺有所区别.这与电机工作原理(线圈的电感等)有关,电机工作时内部线圈产生反电动势直接影响电机的工作效率．因此实际生产的电机是要保证其工作效率的．

5 “浅显”的不可能

有些物理过程的结论本身就具有不确定性,然而不确定中有隐性而“浅显”(理所当然)的约束．比如:如果要求一个物体同要追上另一个物体,这就必然要求后面物体的速度大于前面物体的速度(这个约束关系是“浅显”的)．

图3

例5.如图3所示,在水平面上两个小球A、B质量为m1=2kg，m2=1kg．B静止,A以速度2m/s向右与B发生弹性碰撞．则碰撞后两小球的速度分别是多少?

解析:“碰撞”是关于“动量守恒”应用的实际模型(内力远大于外力)．由于发生弹性碰撞,又满足机械能守恒,故有

m1v1=m1v1′+m2v2′，

联立方程代数求解得

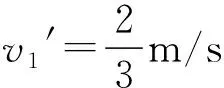
v1′=2m/s和v2′=0(舍去).

舍解的依据:由于碰撞过程中产生的相互作用力是排斥力,即碰撞后B物体一定向右运动且以后不会再发性相互作用了,故不可能出现v2′=0的情况．

被舍解的意义:从数学上看,只是满足两个方程即可,被舍的解实际上是初状态速度情况．

延伸归纳:关于同向追及碰撞情形可能性系列问题中,存在以下“浅显”的不可能情况: (1) 碰撞前后都速度大于前者速度; (2) 碰撞后前者速度小于等于后者速度; (3) 碰撞中机械能不可能增加,也不可能比“完全非弹性碰撞”情况下损失的机械能更多．

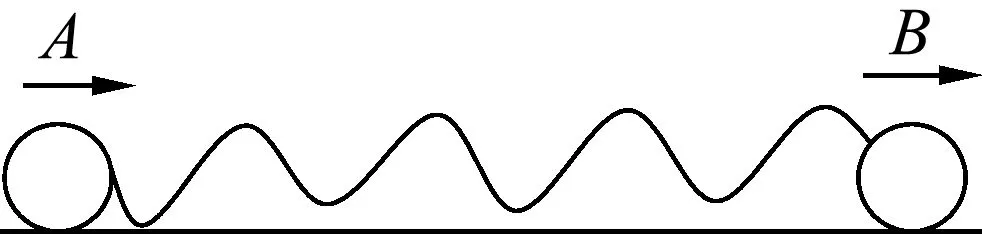
图4

进阶:如图4所示,一根不可伸长的细绳连接A、B两个小球,置于光滑水平面上,mA=2kg,mB=1kg,现给A和B小球提供瞬间初速度,速度分别为vA=2m/s向左,vB=3m/s向右,细绳绷断过程中机械能损失50%．求:细绳绷断后两球的速度．

解析:本题依然是考查动量与机械能的综合问题,建立动量关系与机械能关系即可．

mAvA+mBvB=mAvA′+mBvB′,

取向左为正方向,解得

vA′=1.5m/s,vB′=-2m/s;

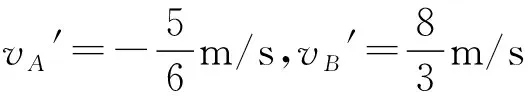
图5

舍解的依据:两小球在背向运动过程导致细绳绷断,细绳绷断一定发生在小球相对远离过程中,因此细绳断后两小球的速度一定是相对远离．而第二解A向右,B向左,即相互靠近,不具实际物理意义．

被舍解的意义:由题设模型可以联立解析中的方程组,但是根据这个方程组无法判断两小球之间的作用方式,而正是由于“绷紧至断”的这种方式使“第二解”舍去．如图5所示,若A球在右,B球在左．其他条件相同而发生相互碰撞．求两球碰后的速度．这个“碰撞”模型与“绷断”模型的数学模型是一样的,在“碰撞”模型中“第二解”就具体实际物理意义,但“第一解”又要“舍去”(碰撞之后相互远离)．

数学是表达物理的一种语言,很多物理理论都是用数学方法进行分析、推理与总结．然而利用数学手段的解决的问题需要结合实际情景,经得起实践的检验,排除没有实际物理意义的解,才能坐实“结论”的科学性,也确定了“论证”的重要性．

参考文献：

1 张健敏.注重对物理题多值的讨论[J].物理教师，2000(12):45-46.

2 周伟玲.例谈对物理问题中数学解的理解与取舍[J].物理实验(中学部分)，2004(2):10-11.