由2016年江苏省高考物理压轴题引起的讨论
陈 雁
(镇海教师进修学校,浙江 315200)
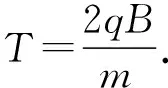
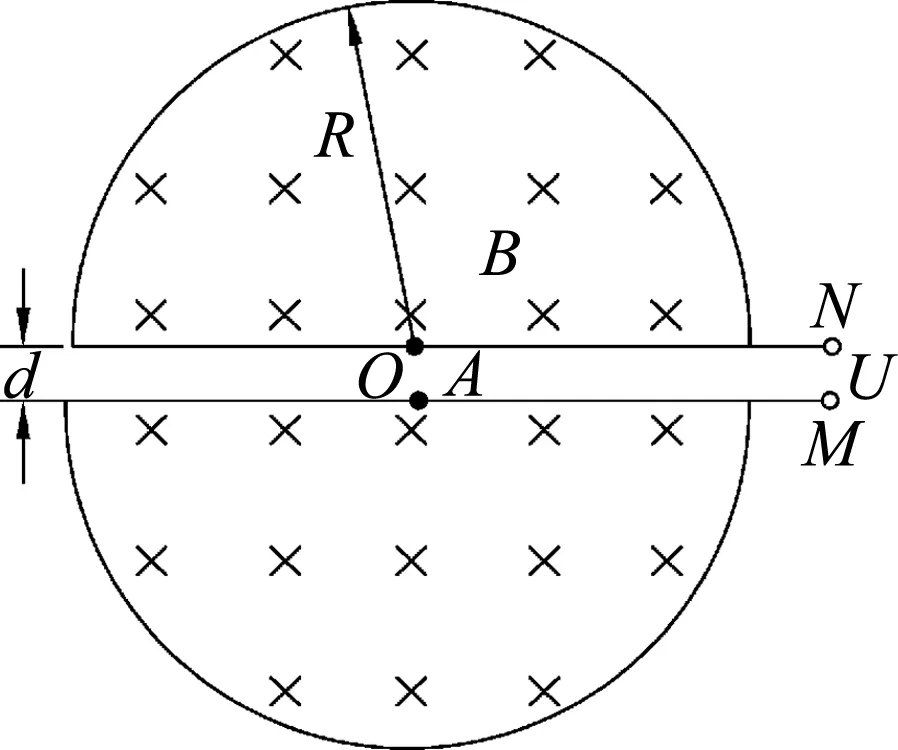
图1图2
(1) 出射粒子的动能Em;
(2) 粒子从飘入狭缝至动能达到Em所需的总时间t0;
(3) 要使飘入狭缝的粒子中有超过99%能射出,d应满足的条件.
参考答案: 当粒子运动半径为R时,粒子出射,有
又
解得
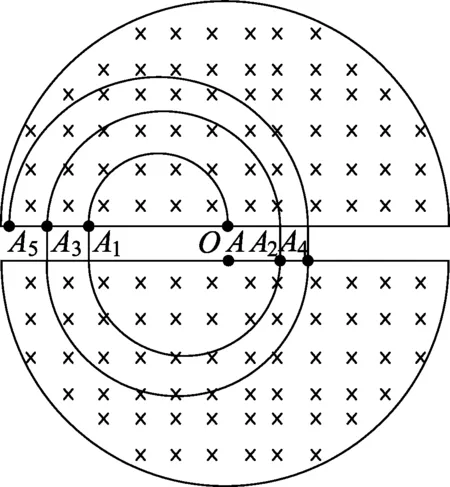
图3 粒子在回旋加速器中运动轨迹
本题的第(1)个小问题:求出射粒子的动能Em,这是比较容易求解的问题.但是,如果我们仔细观察题中的示意图,发现题中A点的位置与圆心O相对,位于D形金属盒的中心处.画出粒子在回旋加速器中运动的轨迹后,如图3所示,自然而然会产生疑问.
1 问题提出
(1) 粒子出射的位置在哪里?
(2) 粒子出射时的半径等于D型金属盒的半径R吗?
(3) 粒子在回旋加速器中加速的次数是多少?
由图3,直接可得出粒子出射的位置应该在O点的左侧,且出射时的半径小于D型盒的半径R.
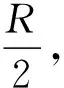
我们知道要获得高能量的带电粒子,粒子在回旋加速器中,不可能只加速1次,必须经过多次加速.带电粒子在回旋加速器中,加速的次数大约是多少.
本文就这3个问题进行分析讨论.
2 问题讨论
2.1 粒子出射时的位置在哪里?
图3为A点飘入狭缝的粒子进入回旋加速器后的运动轨迹,由图3粒子的轨迹图我们可以直接得出结论:粒子出射的位置一定在D型金属盒的左侧.
粒子从A点飘出,经过一次加速,由O点进入D型金属盒,受洛伦兹力作用,作半径为R1的匀速圆周运动.经过半周后,再次进入两盒间缝隙,再次被加速,作半径为R2的匀速圆周运动,如此,粒子在做圆周运动的过程中一次一次地经过盒缝,每次经过盒缝,粒子被加速,粒子的速度越来越大.
设粒子被n次加速后,速度达到vn,在磁场中运动的半径为rn,由
和
得
(1)
由此式可知,轨道半径和加速的次数n的平方根成正比,随着加速次数的增多,轨道半径也越来越大.轨道半径大于等于金属盒半径R时,粒子一定能从盒中射出,没有问题.然而从图3可以看到,粒子的入射点是盒的圆心,粒子在盒中作圆周运动时,其轨道的圆心显然不是D型金属盒的圆心,而是在D型金属盒圆心的左侧.
由图中直观看出,粒子运动到左侧时,离圆心O点的距离大,粒子的出射位置应该在O点的左侧.下面通过计算,得到粒子出射点的位置.
如表1所示,A1为粒子第1次加速后运动到缝隙处的位置,A2为粒子第2次加速后运动到缝隙处的位置,A3为粒子第3次加速后运动到缝隙处的位置,以些类推,An为粒子经过n次加速后运动到缝隙处的位置.由图中可知,n为奇数时,粒子位置在O点的左侧,n为偶数时,粒子位置在O点的右侧.

表1
比较OA2n-1与OA2n,如果OA2n-1>OA2n,粒子一定从O点左侧出射.
用数学归纳法证明OA2n-1-OA2n>0:
当n=1时,
OA1-OA2=2r1-(2r2-2r1)=4r1-2r2=
设n=k时,
OA2k-1-OA2k=2r2k-1-2r2k-2+2r2k-3…2r2+2r1-(2r2k-2r2k-1+2r2k-2…+2r2-2r1)>0;
当n=k+1时,
OA2k+1=2r2k+1-2r2k+OA2k-1,
OA2k+2=2r2k+2-2r2k+1+OA2k,
OA2k+1-OA2k+2=2r2k+1-2r2k+OA2k-1-(2r2k+2-2r2k+1+OA2k)=4r2k+1-2r2k-2r2k+2+OA2k-1-OA2k,
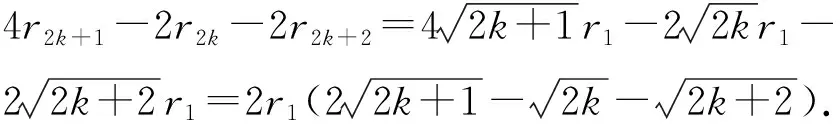
设
有
整理得
4k2+4k+1>4k2+4k
成立,OA2n-1-OA2n>0成立,OA2n-1>OA2n.
由此,我们得出结论,本题中,带电粒子一定从金属盒的左边射出,也即粒子一定是经过奇数次加速后从金属盒O点左侧出射.
2.2 粒子出射时的半径等于D型金属盒的半径R吗?
粒子出射时,轨道半径有没有可能小于R?
由第1问分析可知
OA2n-1=2r2n-1-2r2n-2+2r12n-3…-2r2+2r1.
(2)
将(1)代入(2)整理得
当OA2n-1>R时,粒子出射,有
r2n-1>
(3)
利用Excel计算出不同加速次数,粒子出射时的半径值,列表如表2所示.
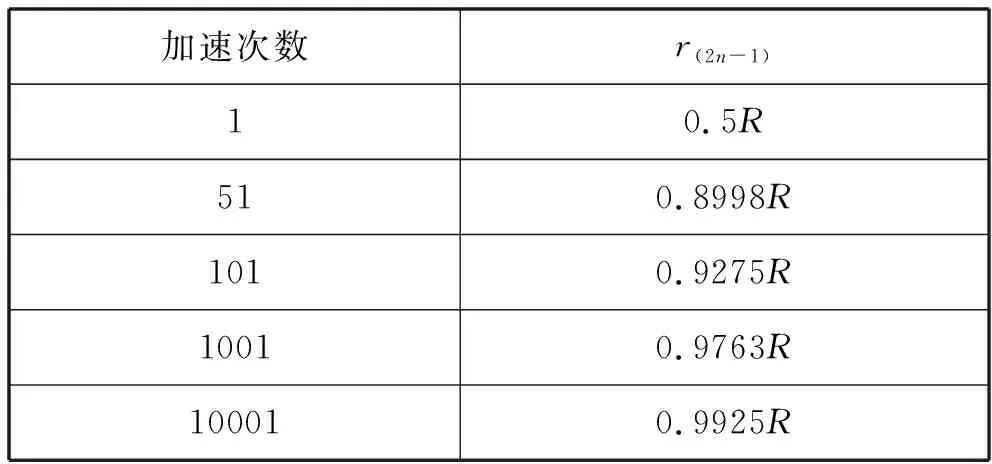
表2 加速次数与粒子出射半径值
从计算结果可以看出,加速次数越多,粒子出射的半径越接近金属盒的半径,但始终小于D型金属盒的半径R.
2.3 粒子在回旋加速器中加速的次数
粒子在回旋加速器中,要经过多次加速,让粒子的能量达到一个比较大的值后,才让粒子从盒中射出.那么,粒子在回旋加速器中,加速的次数是多少呢?
以世界上第1台回旋加速器为例,加速电压为2kV,加速氘离子达到80keV,加速40次数.根据(3)式,利用Excel计算出粒子出射时的半径r41=0.8890R,明显小于加速器金属盒半径;随后建造的第2台25cm直径的较大回旋加速器,其被加速粒子的能量可达到1MeV,假设加速电压没有提高,加速α粒子,那么加速250次数,出射时的半径r251=0.953R.从这2台回旋加速器来看,带电粒子在回旋加速器中加速的次数都不是一个很大的数,因此,粒子出射时的轨道半径明显小于D型金属盒的半径.
人教社出版的普通高中课程标准实验教科书3-1中,关于回旋加速器有这样的描述:回旋加速器加速的带电粒子,能量达到25~30MeV后,就很难再加速了.原因是,按照狭相对论,粒子的质量随着速度的增加而增大,其质量的变化导致其回旋周期的变化,从而破坏了与电场变化周期的同步.
回旋加速器加速的带电粒子,能量可以达到25~30MeV.初步估算带电粒子在回旋加速器中加速的次数.设加速电压为10kV,加速α粒子达到30MeV的能量,要加速1500次,粒子出射的半径等于0.9806R,这个值可以近似等于R.
3 结束语
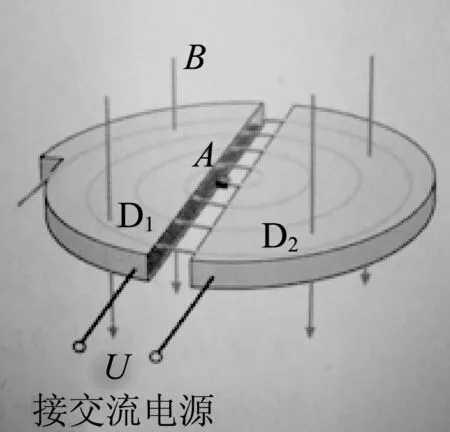
图4
图4是人教社出版的普通高中课程标准实验教科书物理选修3-1中,回旋加速器的插图.图中的回旋加速器上标出“粒子的出射口”,画出了粒子的运动轨道.显然粒子出射时的半径是不等于D型金属盒的半径,明显小于D型金属盒的半径R,粒子作圆周运动的圆心也不是D型金属盒的中心.如果学生对教材中回旋加速器图的印象深刻,那么,在解题时,会产生疑问;如果学生在解本题时,仔细画图,也会在求解中产生疑问,即粒子出射时的半径是否等于D型金属盒的半径.
本题源于经典,又进行了变化拓展.第2、第3小题的设问,撇开了繁杂的运动分析和数学计算,新颖巧妙,充分体现了物理的简洁性和思想性,考查了学生分析解决问题的综合能力.建议在题干中直接写明粒子出射时的半径为R,配图采用教材中的原理图,以消除学生在解题时产生的不必要的疑问.

