理论教学与观测实践的融合——以月地距离的测量为例

米立功

(黔南民族师范学院物理与电子科学学院天文系,贵州 都匀 558000)

星空是最好的实验室,天文学中很多自然规律的发现都是基于大量的实验与观测数据,例如学生熟知的开普勒行星运动定律与万有引力定律.从本质上说,理论源自观测或实验,而学生在教课书中学习的往往是比较成熟的理论知识,在教学过程中,为了培养学生的创新能力与科学探索的精神,将理论教学与观测实践结合起来是必要的.本文以月地距离的理论计算与测量为案例探讨理论教学与观测实践的融合.

1 月地距离的理论计算

在人教版《物理·必修2》中介绍了牛顿做过的著名的“月地检验”,通过“月地检验”证明了地面物体所受地球的力与月球绕地球运转受到的力以及太阳、行星间的力遵从相同的规律,即万有引力定律

(1)

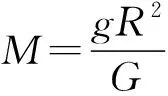
(2)

设月球绕地球运转的加速度为a,地球的半径及月地距离分别为R和d,则根据上式可得

(3)

目前,已经测得地球的平均半径R=6371.03km,地面重力加速度g=9.8m·s-2,地月距离d=3.84×108m,利用上式就可计算月球绕地球公转的加速度.事实上,正如教材中指出:“在牛顿的时代,自由落体加速度已经能够比较精确地测定,当时也能比较精确地测定月球与地球的距离、月球公转的周期,从而能够算出月球运动的向心加速度”.

(4)

从中我们可以发现,在已知重力加速度g与地球半径R的前提下,我们可以通过观测月球绕地球的公转周期T来求月地距离.常识告诉我们,月球在绕地球公转的同时随着地球一起绕太阳公转,月亮会发生盈亏变化,即月相变化,因此,古人通过观测月球的月相变化周期T′来求月球绕地球的公转周期T.已知地球的公转周期是365.25天,则月球绕地球的公转周期可以通过下面的公式得到1/T=1/T′+1/365.25.[2]通过观测,发现月相变化的周期为29.53天,则利用上式可计算出月球的公转周期为27.32天.进一步,利用公式(3),我们也可以得到卫星绕地球公转所遵循的开普勒第三定律

(5)

这里k是对所有卫星都相同的常数.利用开普勒第三定律,我们亦可计算卫星或行星到中心天体的距离.

2 月地距离的直接测量

现代有多种方法可以测量月地的距离,例如,利用激光测距或雷达技术,通过向月球发射脉冲激光束或雷达脉冲,然后接收月球反射回来的脉冲波,根据发射及返回的脉冲波之间的时间间隔,可以计算月地距离.文献[3-4]也给出了一种近似测量月地距离的课堂实验.下面,我们主要介绍利用三角视差法测量月球到地心的距离.

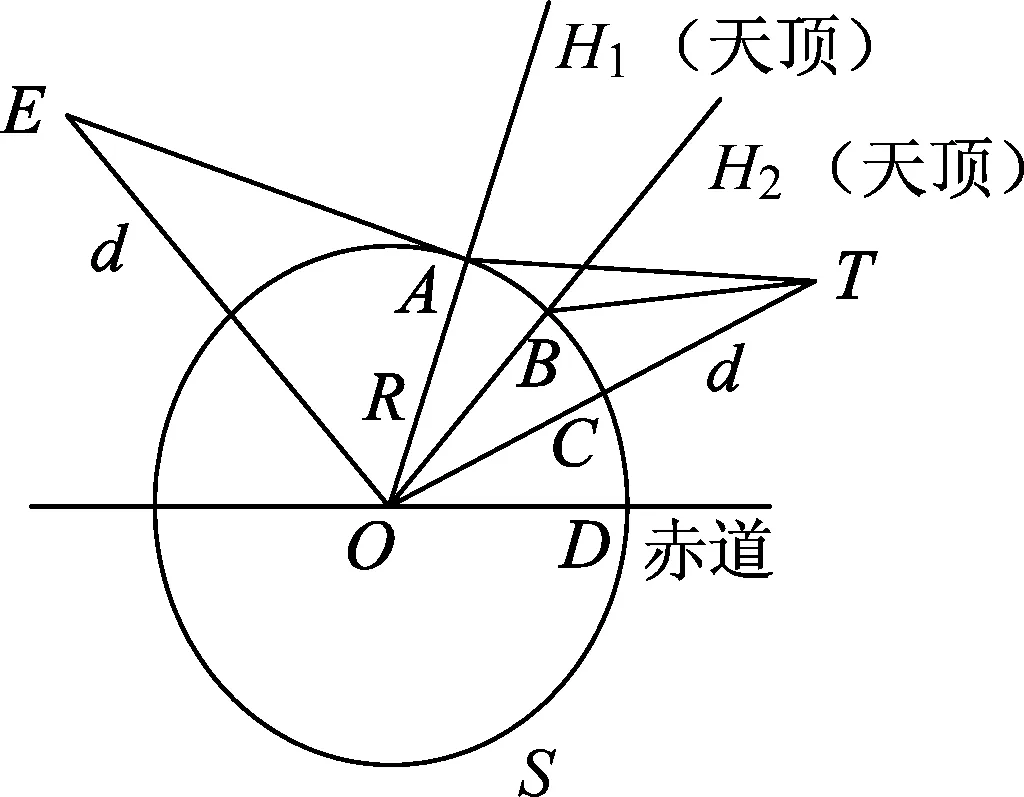
图1 月球的视差图

如图1所示,S是过观测点A、B的经线圈,地球半径OA=OB=R,月球到地心的距离OE=OT=d.设观测点A、B两点的天顶距分别为∠H1AT=Z1，∠H2BT=Z2,地理纬度分别为∠AOD=φ1,∠BOD=φ2,OA、OB在月亮T处的张角(周日视差)分别为∠ATO=α1，∠BTO=α2.

当月亮在地平E处时,它的周日视差∠TOD=θ达到最大,称为周日地平视差,设月亮的周日地平视差∠AEO=P,则月亮到地心的距离为

(6)

根据正弦定理

(7)

(8)

于是

(9)

月球到地心的距离d远大于地球的半径R,即天体的周日视差α1,α2很小,此时,有sinα1≈α1,sinα2≈α2.设地心到月球的距离OT与赤道的夹角∠TOD=θ,则根据三角形的外角定理,α1≈Z1-(φ1-θ),α2≈Z2-(φ2-θ),进一步可得,α1-α2≈Z1-Z2-φ1+φ2,于是

(10)

由公式(10)可知,在已知地球半径与两地观测点地理纬度时,可以通过测量两地月亮的天顶距来计算月亮到地心的距离．

3 总结

事物之间都是相互联系的,物理规律所描述的就是表征事物或事物之间的物理量之间的某种特定的联系,对于这些物理量而言,有些是可以直接测量的,有些则要利用可直接测量的物理量在理论的指导下进行推算.因此,在理论知识与观测实践相结合的教学过程中至少要明确两点,首先,要明确哪些物理量是可以通过实验得到的,其次要明确直接测量的物理量或间接测量的物理量与无法或难以测量的抽象的物理量之间的联系.在明确这两点的前提下,我们可以通过设计实验对可观测的物理量进行测量.如果能将物理量之间的联系与物理现实之间的联系融合起来,用联系的观点指导教学,相信对培养学生正确的科学观与探索精神将会起到很大的帮助.

参考文献：

1 P J Mohr, D B Newell, B N Taylor. CODATA recommended values of the fundamental physical constants: 2014[J]. Rev Mod Phys, 2016, 88(3): 035009.

2 刘学富. 基础天文学[M](1版).北京:高等教育出版社,2004.

3 E Roger Cowley, H B David, 王祖滇. 测定月—地距离的课堂实验[J]. 物理教师, 1993(4):34-34.

4 储文启.用自制仪器测月地间距离[J].物理教师，1988(01)：40-41.