“球槽模型”的数理解析和一个错误的澄清

陈向正 李 力 张贵华

(1. 重庆市清华中学，重庆 400054; 2. 重庆市实验中学，重庆 401320)

如图1所示的“球槽模型”中,质量为M的光滑半圆形槽置于光滑水平面上,质量为m的小球从与圆心等高的右端静止释放.通常大家认为,当小球运动到圆弧最低点时,小球的速率取得最大值.其实,正如文献[1]所指出,这是一个错误认识.文献[1]在推导出小球速率随位置变化的函数表达式后,用数学软件画出槽、球的质量比取不同的参数时小球的速率函数图像,发现“只有当槽的质量为小球的2.73倍以上时,小球在最低点才有最大速度”.[1]

图1

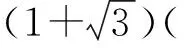
各量如图1所示,对球槽系统分别由水平总动量守恒和机械能守恒定律得

mv2x=Mv1.

(1)

(2)

又小球相对槽的速度方向沿圆弧切向,有

v2ytanθ=v2x+v1.

(3)

v22=v2x2+v2y2.

(4)

令k=M/m,则可得

(5)

(6)

其中A=k+k2+(1+k)2cot2θ.

从(5)式容易看出,在θ∈[0,π/2]内,v1随θ的增加而单调增加,故θ=π/2(即球在圆弧最低点)时槽的速率最大.但(6)式中球的速率v2的单调性则复杂得多.为简便计,我们等价地考虑下面函数f(θ)的单调性.

(7)

f′(θ)=cosθ-

(8)

在θ∈[0,π/2]内f(θ)是广义增函数[2](即不减函数)的充要条件是f′(θ)≥0,[2]因θ∈[0,π/2]内cosθ≥0,故只需上式中{…}≥0,即

A2≥kA+2k(1+k)2/sin2θ.

(9)

移项后提公因式有

[k2+(1+k)2cot2θ]A≥2k(1+k)2/sin2θ,

两边同乘sin4θ,有

[k2sin2θ+(1+k)2cos2θ][(k+k2)sin2θ+(1+k)2cos2θ]≥2k(1+k)2sin2θ.

即

[k2+(1+2k)cos2θ]A≥2k(1+k)2sin2θ.

(10)

[k2+(1+2k)cos2θ]A=2k(1+k)2sin2θ.

(11)

在上式两边同除以(1+k),同时令x=cos2θ≥0,则(11)式变为

[k2+(1+2k)x]·(k+x)=

2k(1+k)(1-x).

(12)

化为标准形式有

(2k+1)x2+k(5k+3)x+C=0，

(13)

其中C=k(k2-2k-2).

得到

x=cos2θ=

x=cos2θ=

(14)

于是得到下列命题

它与质量比参数k的取值有关.

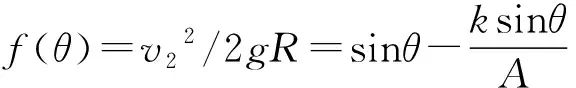
图2

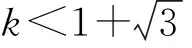
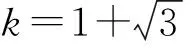
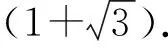
图3

参考文献：

1 张燕怡.关于力学综合常见模型“球槽问题”的一点讨论 [J].物理教学探讨,2017(4):52-52,61.

2 菲赫金哥尔茨.微积分学教程(第一卷)(第8版)[M].北京:高等教育出版社,2016:107,228.