风电偏航制动器制动稳定性研究
高震, 郑建新(河南理工大学机械与动力工程学院,河南焦作454003)
0 引言
风电是使用最为广泛和发展最快的可再生能源之一。在风机正常运行时,由于风向经常发生变化,风力发电机需要自动偏航对风,偏航和制动动作较为频繁。来自国内风电场的统计资料表明,风电机组在偏航过程中经常产生异常振动并伴随极强噪声,成为风电机组的严重质量隐患之一[1-3]。
偏航过程中的振动是由偏航制动器制动块和制动盘之间的相互摩擦引起[4-5]。这种由制动干摩擦激励偏航制动系统弹性模态产生的失稳振动现象严重影响着风电机组和偏航驱动电机的稳定工作。而避免偏航振动发生的有效方法是从研究失稳振动机理出发,找出偏航振动的影响因素并进行有效控制。廖明夫等[6]建立了塔架扭转振动的模型,基于扭振运动方程,引入了摩擦失稳因子,得到了塔架扭振失稳条件。Kang[7]建立了有限元制动尖叫模型,分析了非对称制动盘对非线性制动尖叫的影响。李晓光等[8-9]建立了兆瓦级风机偏航系统低速振动运动学特性模型,发现了导致低速抖动的因素,并提出了消除低速抖动的技术措施。Do等[10]采用数值分析方法研究了摩擦参数变化引起的振动问题。李小彭等[11]通过建立汽车盘式制动系统的二自由度动力学模型,研究了制动初速度、制动压力、阻尼和刚度等因素对制动系统动态特性的影响。
对于风电偏航制动振动问题,国内外许多学者进行了研究,并取得了成果[12-15],但在研发抗颤振风电偏航制动器时如何更直观快捷地进行选择材料和设计结构还需进一步研究。本文将从摩擦学角度研究风力发电机偏航系统的失稳振动机理,建立偏航制动系统动力学模型,找出制动过程中导致失稳振动的影响因素和临界失稳条件,并通过MATLAB绘制稳定性曲面图,为研发抗颤振偏航制动器和抑制风电偏航制动过程中的失稳振动提理论依据。
1 偏航制动系统动力学模型
风机在偏航制动过程中,偏航减速器带动制动盘以角速度ω做匀速圆周运动。由于偏航制动器上的制动块与制动盘之间的摩擦状态变化(在静、动摩擦之间转换),摩擦力会影响制动盘的运动,形成速度反馈,进而造成制动盘转速忽快忽慢。
考虑到制动块相对于驱动装置的运动速度是恒定的,为便于描述制动盘与制动块之间的运动关系,假设偏航过程中偏航系统驱动装置静止,而制动块以角速度ω做匀速圆周运动,驱动制动盘做变速运动。在任意瞬时,制动盘与制动块之间的相对运动可简化为直线移动。将制动盘与制动块通过摩擦力耦合在一起,假设制动盘和制动块之间的阻尼系数为c,刚度为k,由此建立偏航时失稳振动力学模型如图1所示。图1中,1为制动块,2为制动盘

图1 偏航制动系统动力学模型
假设制动块作为主动件,以速度v进行运动,制动盘为从动件。制动块缓慢向制动盘移动,移动距离s0后弹簧因压缩产生的驱动力正好等于制动块所受的最大静摩擦力Fs,即Fs=k·s0。此后弹簧继续压缩,制动盘便开始运动。
若制动块开始运动,经时间t后运动的距离为s,则制动盘的运动方程为

式中:m为制动盘的质量;Fk为滑动摩擦力。
低速运动时,动摩擦因数随着速度的增加而降低[16]。为方便分析,将动摩擦力近似分为两个部分:一部分为不变的分量Fc,另一部分随着速度的增加而减小的分量(h为常数),即令静动摩擦力之差ΔF=Fs-Fc,代入式(1)得:

由此获得制动盘的运动方程为

式中:ξ为阻尼比,ξ=(c+h)/2mω0;ω0为系统固有频率;而A和φ由初始条件确定。
当t=0时,有s=s0,s′=0,因而:
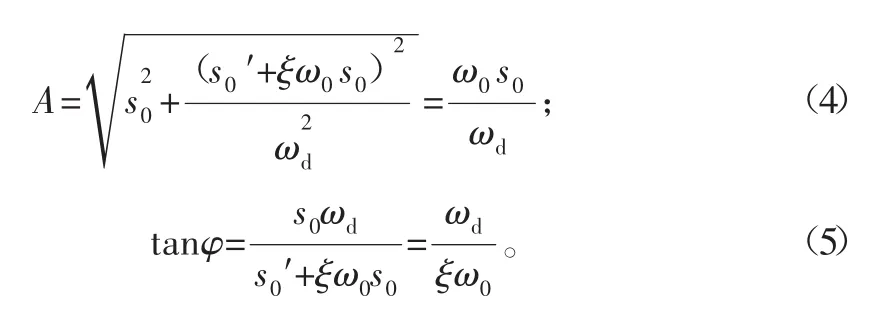
由k·s0=μ·N=μ·p·S知:
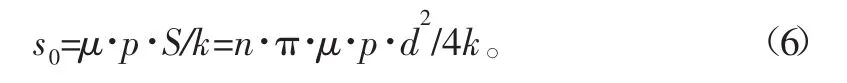
式中:μ为最大静摩擦因数;N为正压力;p为偏航余压;S为偏航余压作用面积;n为活塞数量,d为活塞直径。
2 偏航制动系统稳定性分析
由式(3)确定制动盘的的速度v(t)和加速度a(t)分别为:


制动盘的速度方程表明,制动盘是在匀速运动(速度为v)的基础上叠加了一个振荡运动。
从运动角度来看,只要在偏航过程中制动盘存在瞬时静止,即可判断存在偏航振动。假设在t0时刻,制动盘的速度v(t0)=0,加速度a(t0)=0,由制动盘的运动方程可以得到偏航系统制动过程中的临界失稳速度
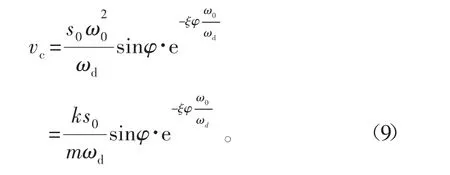
如果偏航速度v低于临界失稳速度vc,偏航制动器在制动的过程中就会出现忽停忽动的非均匀运动,即发生失稳振动。要避免这一现象,偏航速度必须大于临界失稳速度。
式(9)表明,系统的刚度k、固有频率ω0和阻尼比ξ、制动盘与制动块上的摩擦片材料(静摩擦因数μ和动静摩擦因数之差Δμ)、制动盘质量m、活塞直径d与数量n和偏航余压p是导致偏航系统失稳振动的主要因素。
3 偏航制动系统振动控制策略
临界失稳速度模型表明,在偏航制动器使用过程中,若发生失稳振动,则可通过更换制动块上的摩擦片材料(改变摩擦因数μ)和调整偏航余压p两方面来进行振动控制。
由此基于偏航临界失稳速度来研究偏航制动系统振动控制策略。仿真参数设定如下:制动盘质量m=100 kg,系统刚度k=2.5×107N·m/rad,系统阻尼比ξ=0.01,制动器中活塞直径d=0.12 m,数量n=3,偏航余压p=0.2~0.8 MPa,摩擦因数0.2~0.4。
利用式(9)确定静摩擦因数μ、偏航余压p与临界失稳速度vc之间的关系,即偏航制动稳定性曲面图,如图2所示。

图2 稳定性曲面图
图2表明,当偏航余压一定时,摩擦因数越大,临界失稳速度越大;当摩擦因数一定时,偏航余压越大,临界失稳速度也越大。偏航余压和摩擦因数的交互作用对临界失稳速度有影响,且相对于摩擦因数,偏航余压对临界失稳速度的影响更大。
图2中,稳定性曲面上方是偏航速度大于临界失稳速度区域,不会发生失稳振动;而在曲面下方,偏航速度低于临界失稳速度,将发生失稳振动。显然,当制动过程中偏航速度恒定时,若发生失稳振动,则可通过合理减小偏航余压或更换摩擦因数更小的摩擦片来控制振动。
进一步判定稳定性曲面上方是否属于稳定区域,在曲面上选取参考点Q(0.6,0.3,0.01202),并在Q点上、下方分别选取U(0.6,0.3,0.015)、L(0.6,0.3,0.009)两点。由于U点偏航速度高于临界失稳速度,而L点偏航速度低于临界失稳速度,显然U点应处于稳定状态,而L点将发生制动失稳振动。
分析制动盘在U、L两点工况下的运动特性,结果如图3所示。
图3表明,当偏航速度为0.015 m/s时(即U点工况),制动盘在制动过程中速度始终为正,不会出现失稳振动现象。而当偏航速度为0.009 m/s时(即L点工况),制动盘在制动过程中出现负速度,存在失稳振动现象。
同样可结合稳定性曲面图来分析其他参数对临界失稳速度的影响,以此来解决偏航制动过程中的失稳振动问题,在此不再赘述。
而在研发抗颤振风电偏航制动器时,应根据制动器使用工况,基于制动盘和临界失稳速度采用稳定性曲面图法来考虑制动器的结构设计和材料选择,对系统的刚度k、固有频率ω0和阻尼比ξ,摩擦片材料(确定静摩擦因数μ)和活塞直径d与数量n提出要求。
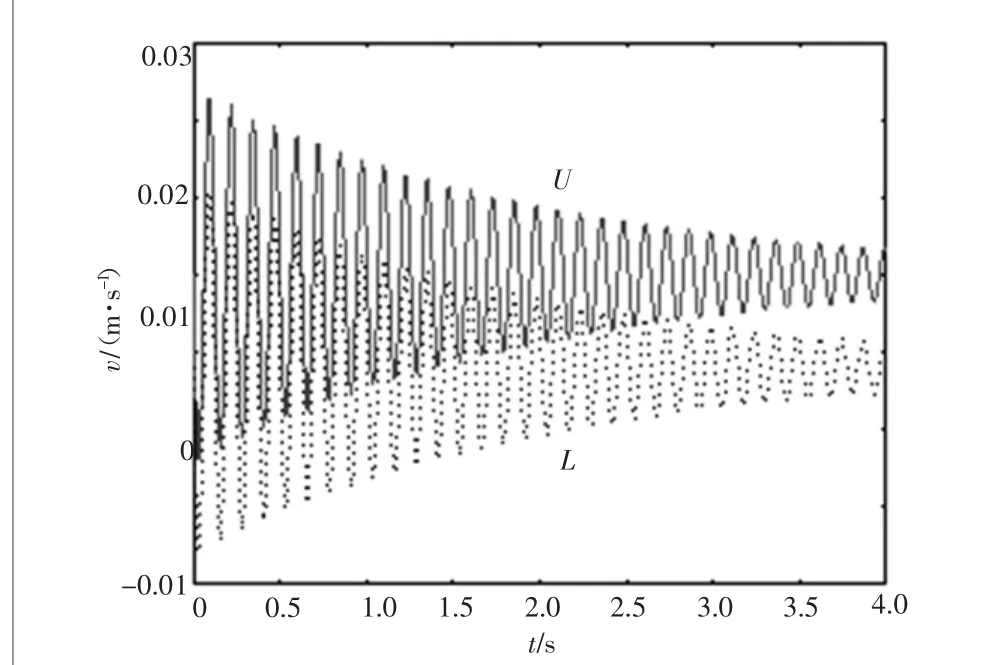
图3 不同偏航速度下的制动盘运动速度
4 结论
1)系统的刚度、固有频率和阻尼比、制动盘与制动块上的摩擦片材料、制动盘质量、活塞直径与数量和偏航余压是导致偏航系统失稳振动的主要因素。
2)当偏航过程中发生失稳振动时,可通过减小偏航余压或更换摩擦因数更小的摩擦片来控制振动。
3)研发抗颤振风电偏航制动器时,应结合临界失稳速度和并基于制动盘进行制动器结构设计和选材,通盘考虑系统的刚度、固有频率和阻尼比,摩擦片材料和活塞直径与数量。
[1]LIN Yonggang,TU Le,LIU Hongwei,et al.Fault analysis of wind turbines in China[J].Renewable and Sustainable Energy Reviews,2016,55:482-490.
[2]刘波,贺志佳,金昊.风力发电现状与发展趋势[J].东北电力大学学报,2016,36(2):7-13.
[3]沈小军,杜万里.大型风力发电机偏航系统控制策略研究现状及展望[J].电工技术学报,2015,30(10):196-203.
[4]李莉,尹东晓,张立军.盘式制动器制动抖动现象机理研究[J].汽车工程,2006,28(4):361-365.
[5]JACOBSSON H.Aspects of Disc Brake Judder[J].Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering,2003,217(6):419-430.
[6]廖明夫,黄巍,董礼.风力机偏航引起的失稳振动[J].太阳能学报,2009,30(4):488-492.
[7]KANG J.Automotive brake squeal analysis with rotating finite elementsofasymmetricdiscintime[J].JournalofSound&Vibration,2017,393:388-400.
[8]李晓光,赵萍,韩德海.主动偏航过程兆瓦级风机偏航系统失稳振动特性[J].中南大学学报(自然科学版),2013,44(3):949-954.
[9]李晓光,赵萍.兆瓦级风机偏航系统低速抖动运动学特性[J].中南大学学报(自然科学版),2013,44(1):89-94.
[10]DO H Q,MASSA F,TISON T,et al.A global strategy for the stability analysis of friction induced vibration problem with parameter variations[J].Mechanical Systems&Signal Processing,2017,84:346-364.
[11]李小彭,李加胜,李木岩,等.盘式制动系统参数对制动颤振的影响分析[J].振动,测试与诊断,2017,37(1):102-107.
[12]宋彦.伺服系统提高速度平稳度的关键技术研究与实现[D].长春:中国科学院长春光学精密机械与物理研究所,2010:3-15.
[13]宁国宝,张立军,尹东晓,等.制动引起的方向盘抖动现象试验研究[J].中国工程机械学报.2004,2(3):355-359,374.
[14]KANG J,CHOI S.Brake dynamometer model predicting brake torque variation due to disc thickness variation[J].Drive System Technique,2007,221(1):49-55.
[15]JUNG S P,PARK T W,CHAI J B,et al.Thermo-mechanical finite element analysis of hot judder phenomenon of a ventilated disc brake system[J].International Journal of Precision Engineering&Manufacturing,2011,12(5):821-828.
[16]王国强,马若丁,刘巨元,等.金属摩阻材料间摩擦因数与滑动速度的关系研究[J].农业工程学报,1997,13(1):36-38.(责任编辑 邵明涛)

