单轴应变锗带隙特性和电子有效质量计算
底琳佳, 戴显英, 苗东铭, 吴淑静, 郝 跃
(1. 西安电子科技大学 微电子学院,陕西 西安 710071;2. 西安电子科技大学 宽带隙半导体国家重点学科实验室,陕西 西安 710071)
单轴应变锗(Ge)具有载流子迁移率提升高、与硅(Si)集成工艺兼容等优势,在Si基高迁移率器件与集成电路应用方面引起了人们的广泛关注[1-3].能带结构是进一步研究应变Ge电学、光学性能的理论基础,而k·p方法不仅具有高效的计算效率,且能够准确地描绘出在布里渊区给定点附近的导带和价带结构,通常用于计算载流子的有效质量和运输特性.
目前,针对应变Ge能带结构和运输特性的研究主要集中在价带和空穴迁移率增强方面[4-5],关于导带结构,特别是与电子散射和运输密切相关的有效质量的理论研究相对较少.此外,已有研究表明双轴应变Ge可以从间接带隙转变为直接带隙半导体,并具有与Ⅲ-Ⅴ化合物半导体相比拟的光增益,可用于光电子器件的设计[6-7].与双轴应变相比,单轴应变具有一些显著的优点,例如,在高垂直电场下维持空穴迁移率增益,为纳米级短沟道器件提供大的驱动电流提升等[8].因此,有关单轴应变Ge是否存在带隙转换以及单轴应力如何影响电子输运的研究具有重要的意义.
笔者采用30k·p方法,计算了不同单轴应力(方向、类型和量级)作用下Ge的能带结构,定量分析了Ge导带能谷分裂与偏移、纵向和横向电子有效质量及电子态密度有效质量随应力的变化情况.
1 30 k·p方法
应变系统的薛定谔方程可由下式表征[9]:
(1)
其中,p=-i(h/(2π)),为动量算符,m为自由电子质量,V0(r)为未形变晶格的周期势,i、j代表x、y、z,ε为应变张量.将布洛赫波函数φnk(r)= exp(ik·r)unk(r) 代入式(1),可得
式(2)中的哈密顿量即为包含应变效应的k·p哈密顿量.
如果未形变系统哈密顿量的特征值En0及特征函数un0已知,如下式所示:
(5)
可将式(3)中的k·p乘积项及式(4)看作微扰量,并以已知的特征函数为基展开unk,根据微扰理论可以得到一系列k·p久期方程:
式(6)中的前两项用于建立未形变系统的k·p哈密顿矩阵,第3项用于建立应变引起的微扰矩阵.
对于Ge,选取来自[000]、(2π/a)[111]和(2π/a)[200]平面波的15个Γ态[10],并根据群论选择规则可将由式(6)中第2项决定的动量矩阵参数减小到10个:
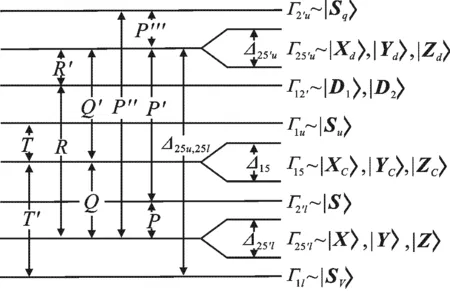
图1 30 k·p模型原理图
此外,由于自旋轨道相互作用的存在,根据15个Γ态所属原子态的不同,可将其分为3类[11]:Γ1l、Γ2′l、Γ1u和Γ2′u属于s原子态,自旋轨道相互作用使它们变为二度简并态;Γ12′属于d原子态,自旋轨道相互作用,使其变为四度简并态;Γ25′l、Γ25′u和Γ15属于p原子态,自旋轨道相互作用使它们分裂为一组四度简并态和一组二度简并态,相应的分裂能分别为Δ25′l、Δ25′u和Δ15,且在Γ25′l和Γ25′u之间存在非零的耦合系数Δ25u,25l.图1给出了30k·p模型的原理图,并列出了相应的Γ态及其对应的原子态波函数、动量矩阵参数、自旋轨道相互作用系数.
因此,根据以上Γ态可以建立包含应变效应的30k·p哈密顿矩阵,因为矩阵形式相对复杂,文中并未列出,相应的矩阵可在文献[12]中找到.根据已有的单轴应变张量模型[13],通过对角化 30k·p哈密顿矩阵可得到单轴应变Ge的能带结构.计算过程中各参数的具体数值列在表1和表2中,由式(7)决定的应变微扰矩阵系数和文献[12]中的一致.

表1 锗在Γ点处的能量本征值及自旋轨道相互作用系数

表2 锗的动量矩阵参数
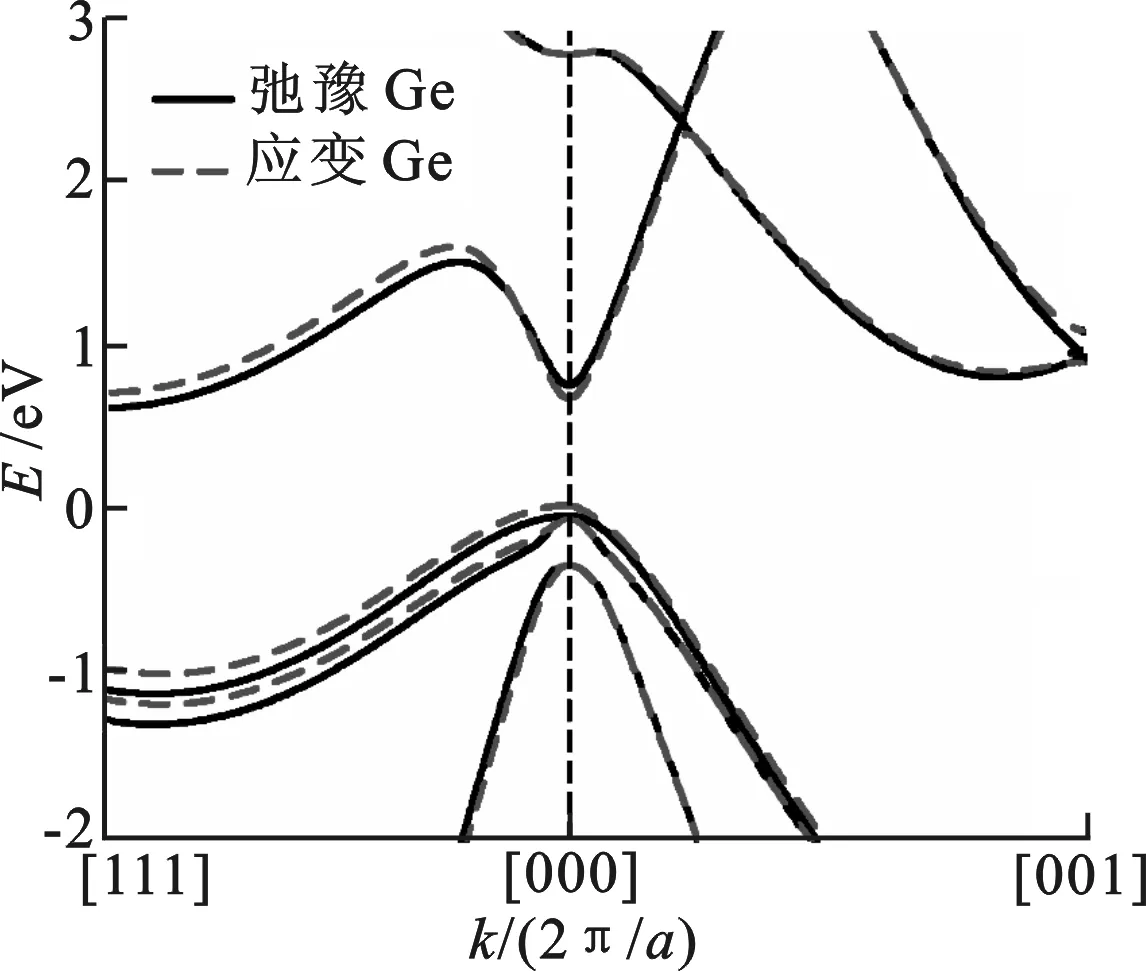
图2 弛豫Ge(实线)和[111]方向2 GPa单轴应变Ge(虚线)能带结构
2 单轴应变Ge带隙特性
图2给出了弛豫Ge(实线)和沿[111]方向的2 GPa单轴应变Ge(虚线)的能带图.对于弛豫Ge,计算得到的L和Δ能谷能量分别为 0.662 eV 和 0.851 eV.从图2可以看出,单轴应变Ge的各能级均发生了明显的偏移和翘曲,说明带隙宽度和有效质量会随着应力而变化.此外,由于应力的引入,晶格对称性遭到破坏,原有的L和Δ能谷简并度将发生改变.

图3 单轴应变Ge导带各能谷随应力的变化情况
值得注意的是,在单轴应力的作用下,Ge导带带边能级会发生改变.图4给出了不同方向单轴应力作用下Ge导带各能谷带隙宽度随应力的变化情况,可以更直观反应带边能级的转换.由图4(a)可见,当沿[001]方向的单轴压应力大于 2.1 GPa 后,导带带边能级变为Δ能谷,但Ge仍为间接带隙半导体;而在张应力作用下,由于Γ能谷带隙宽度随应力增大而减小的趋势远大于L能谷,使得在应力增大到一定程度后,Γ能谷将成为导带带边能级,根据计算结果,当张应力大于 4.8 GPa 后,Ge从原来的间接带隙半导体变为直接带隙半导体,禁带宽度为 0.402 eV.类似地,由图4(c)可见,沿[111]方向的单轴张应力大于 6.2 GPa 后,Ge变为直接带隙半导体,禁带宽度为 0.244 eV.
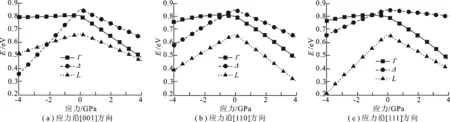
图4 单轴应变Ge导带各能谷带隙宽度随应力的变化情况
文中结果与文献[13]结果不同,这是由于文献[13]未考虑应力作用下高能量能级对导带能谷的影响,且其形变势参数并不充分[6].此外,文献[14]采用第一性原理对张应变Ge能带结构进行了计算,发现[001]和[111]方向单轴张应力均可使Ge由间接带隙转变成直接带隙.文献[15]报道的[001]方向悬浮Ge纳米线结构在产生的5.7% (5.87 GPa) 的单轴张应变作用下,已转变为直接带隙半导体.这些相关结论可以间接验证文中所得结果的准确性.
3 单轴应变Ge电子有效质量
电子有效质量取决于其所处状态下的能带结构,可由下式表征:
(8)
根据单轴应变Ge能带结构,采用二次函数拟合方法可以得到Ge导带各能谷电子有效质量.为了验证计算的有效性,表3列出了实验测量[16]、赝势法[17]、紧束缚法[18]以及文中 30k·p方法计算得到的弛豫Ge导带能谷电子有效质量.表中,ml表示纵向有效质量,mt表示横向有效质量,可以看出,所得结果基本一致.

表3 弛豫Ge导带各能谷电子有效质量
图5分别给出了不同方向单轴应力作用下Ge导带L和Δ能谷纵向、横向有效质量随应力的变化情况.单轴应力破坏了晶体对称性,使导带能谷产生分裂和偏移,有效质量也会随之改变.总体而言,导带L能谷在各方向单轴应力作用下,纵向、横向有效质量变化并不明显,而Δ能谷在[110]、[111]单轴应力作用下有大幅改变,这意味着剪切应力对于Δ能谷的作用比L能谷更为显著.
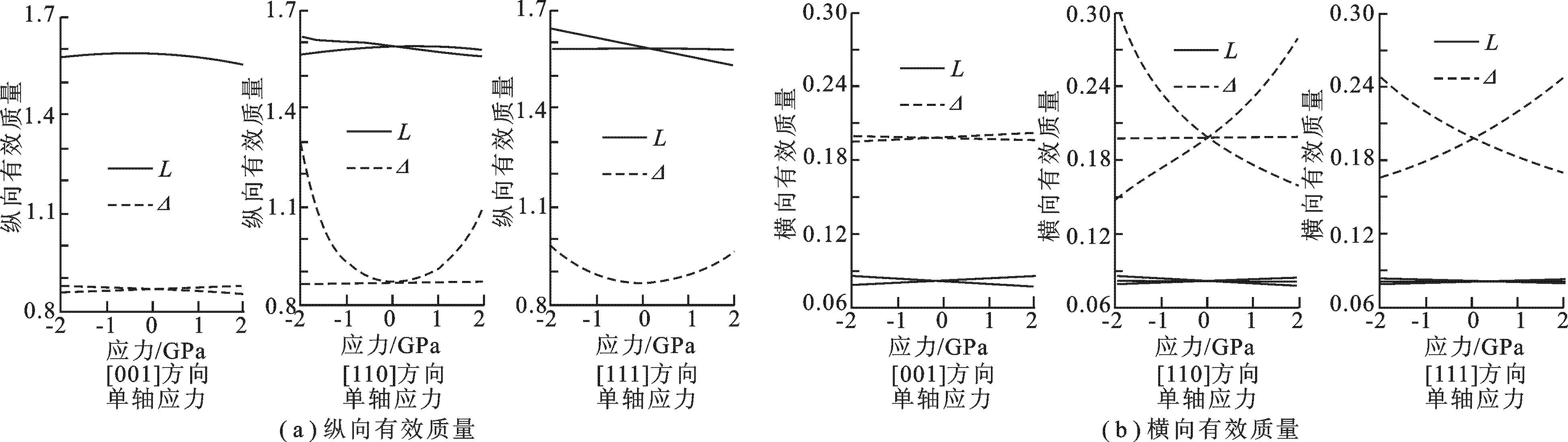
图5 单轴应变Ge导带L、Δ能谷纵向和横向有效质量随应力的变化情况
态密度有效质量与有效状态密度、载流子散射几率密切相关,也是应变Ge的重要参数.应变Ge电子态密度有效质量可由下式给出[19]:
(9)
其中,mc=(mlmt2)1/3为导带某一能谷的态密度有效质量,ΔEc,split为导带能谷分裂能,kB为玻尔兹曼常数,a和b分别表示能级分裂后产生的能量较低能谷的简并度和能量较高能谷的简并度,例如[111]单轴张应力作用下,对于Δ能谷,a、b分别为6、0,对于L能谷,a、b分别为3、1.
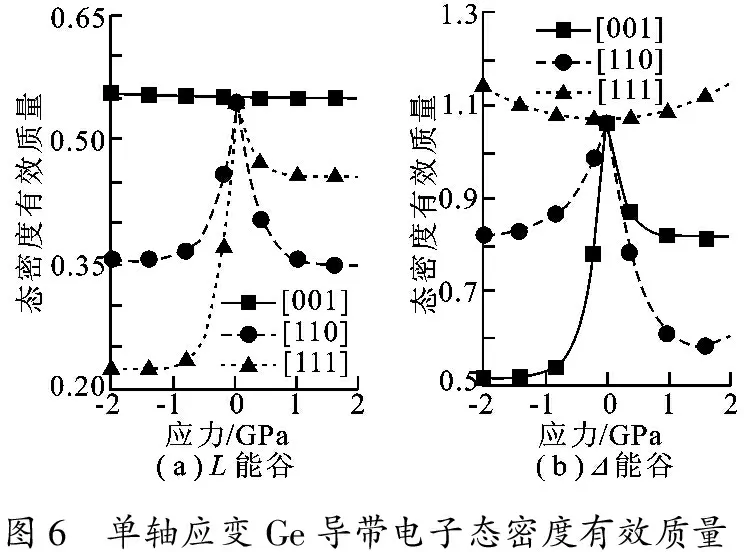
图6 单轴应变Ge导带电子态密度有效质量
图6为不同方向单轴应力作用下Ge导带L和Δ能谷的电子态密度有效质量随应力的变化情况.由图6(a)可见,沿[110]和[111]方向的单轴应力可以有效降低L能谷电子态密度有效质量,并在应力大于 1 GPa 后,趋近为常数,其中沿[111]方向的单轴压应力可使L能谷电子态密度有效质量取得最小值 0.22m0.类似地,由图6(b)可见,Δ能谷的电子态密度有效质量在沿[001]方向单轴压应力大于 1 GPa 后取得最小值 0.52m0.
态密度有效质量的显著降低,是由于单轴应力使导带能谷发生分裂,能级简并度降低,随着分裂能的增大,电子越来越集中于低能量能谷.态密度有效质量的减小,可以有效降低载流子的散射几率,提高迁移率,从这一角度考虑,为了得到更高的电子迁移率,沿[111]方向的单轴压应变Ge可作为N沟道金属氧化物半导体(N-channel Metal Oxide Semiconductor,NMOS)器件导电沟道材料的最佳选择.
4 结 束 语
文中采用30k·p方法,对沿[001]、[110]、[111]方向的单轴应变Ge能带结构进行了计算.单轴应力的引入使得各能级发生不同程度的翘曲与偏移,进而改变了单轴应变Ge的带隙特性和电子有效质量.结果表明:在[001]、[111]方向单轴张应力作用下,Ge由间接带隙转变为直接带隙,带隙性质的转变使得单轴应变Ge可用于光电集成器件; 导带L和Δ能谷电子纵向、横向有效质量并不明显地依赖于单轴应力,但沿[111]和[001]方向的单轴压应力可分别使L和Δ能谷态密度有效质量取得最小值,这有利于减小电子散射几率,提升电子迁移率.所得相关结论可为设计高性能单轴应变锗器件应力和沟道方向选择提供理论参考.
[1] LIU Y, NIU J B, WANG H J, et al. Strained Germanium Quantum Well PMOSFETs on SOI with Mobility Enhancement by External Uniaxial Stress[J]. Nanoscale Research Letters, 2017, 12(1): 120-124.
[2] LEE C F, HE R Y, CHEN K T, et al. Strain Engineering for Electron Mobility Enhancement of Strained Ge NMOSFET with SiGe Alloy Source/Drain Stressors[J]. Microelectronic Engineering, 2015, 138(C): 12-16.
[3] LIU J S, CLAVEL M B, HUDAIT M K. An Energy-efficient Tensile-strained Ge/InGaAs TFET 7T SRAM Cell Architecture for Ultralow-voltage Applications[J]. IEEE Transactions on Electron Devices, 2017, 64(5): 2193-2200.
[4] MA J L, FU Z F, LIU P, et al. Hole Mobility Enhancement in Uniaxial Stressed Ge Dependence on Stress and Transport Direction[J]. Science China: Physics, Mechanics and Astronomy, 2014, 57(10): 1860-1865.
[5] 白敏, 宣荣喜, 宋建军, 等. 压应变Ge/(001)Si1-xGex空穴散射与迁移率模型[J]. 物理学报, 2015, 64(3): 038501-038506.
BAI Min, XUAN Rongxi, SONG Jianjun, et al. Hole Scattering and Mobility in Compressively Strained Ge/(001)Si1-xGex[J]. Acta Physica Sinica, 2015, 64(3): 038501-038506.
[6] KURDI M E, FISHMAN G, SAUVAGE S, et al. Band Structure and Optical Gain of Tensile-strained Germanium Based on a 30 Bandk·pFormalism[J]. Journal of Applied Physics, 2010, 107(1): 013710-013717.
[7] TANI K, SAITO S, ODA K, et al. Room-temperature Direct Band-gap Electroluminescence from Germanium(111)-Fin Light-emitting Diodes[J]. Japanese Journal of Applied Physics, 2017, 56(3): 032102.
[8] DAI X Y, SHAO C F, HAO Y. Uniaxially Strained Silicon on Insulator with Wafer Level Prepared by Mechanical Bending and Annealing[J]. Applied Physics Express, 2013, 6(8): 081302.
[9] SUN Y, THOMPSON S E, NISHIDA T. Strain Effect in Semiconductors:Theory and Device Applications[M]. New York: Springer, 2010: 118.
[10] CARDONA M, PQLLAK F H. Energy-band Structure of Germanium and Silicon: thek·pMethod[J]. Physical Review, 1966, 142(2): 530-543.
[11] RICHARD S, ANIEL F, FISHMAN G. Energy-band Structure of Ge, Si, and GaAs: a Thirty-bandk·pMethod[J]. Physical Review B, 2004, 70(23): 18976-18984.
[12] RIDEAU D, FERAILLE M, CIAMPOLINI L, et al. Strained Si, Ge, and Si1-xGexAlloys Modeled with a First-principles-optimized Full-zonek·pMethod[J]. Physical Review B, 2006, 74(19): 195208-195227.
[13] 戴显英, 李金龙, 郝跃. 应变锗的导带结构计算与分析[J]. 西安电子科技大学学报, 2014, 41(2): 120-124.
DAI Xianying, LI Jinlong, HAO Yue. Calculation and Analysis of the Conduction Band-structure of Strained Germanium[J]. Journal of Xidian University, 2014, 41(2): 120-124.
[14] LIU L, ZHANG M, HU L, et al. Effect of Tensile Strain on the Electronic Structure of Ge: a First-principles Calculation[J]. Journal of Applied Physics, 2014, 116(11): 113105.
[15] SUKHDEO D S, NAM D, KANG J H, et al. Direct Bandgap Germanium-on-Silicon Inferred from 5.7%100Uniaxial Tensile Strain[J]. Photonics Research, 2014, 2(3): A8-A13.
[16] MADELUNG O, RÖSSLER U, SCHULZ M. Semiconductors·Group Ⅳ Elements, Ⅳ-Ⅳ and Ⅲ-Ⅴ Compounds. Part b - Electronic, Transport, Optical and Other Properties[M]. Berlin: Springer, 2002: 2854.
[17] KIM J, FISCHETTI M V. Electronic Band Structure Calculations for Biaxially Strained Si, Ge, and Ⅲ-Ⅴ Semiconductors[J]. Journal of Applied Physics, 2010, 108(1): 013710.
[18] NIQUET Y M, RIDEAU D, TAVERNIER C, et al. Onsite Matrix Elements of the Tight-binding Hamiltonian of a Strained Crystal: Application to Silicon, Germanium, and Their Alloys[J]. Physical Review B, 2009, 79(24): 245201-245213.
[19] SONG J J, CHAO Y, ZHANG H M, et al. Longitudinal, Transverse, Density-of-states, and Conductivity Masses of Electrons in (001), (101) and (111) Biaxially-strained-Si and Strained-Si1-xGex[J]. Science China: Physics, Mechanics and Astronomy, 2012, 55(11): 2033-2037.

