《小数乘整数》教学的典型学习资源分析及利用策略
◆陶红强
关于小数乘整数,笔者听了很多节教研课,发现学生有很多典型的资源。这些学生的资源反映了学生一定的认知水平和认知观念。仔细分析这些资源背后的原因,有利于我们教师精准地诊断学生的思维,特别是学生所遇到的困难,进而更有效地运用这些资源。基于以上思考,本文将这些典型的资源做了一些整理,并进行了分析,在此基础上提出一些对策。
一、基于算法的分析
(一)典型资源

(二)原因分析
对上述学生出现的5个典型的学习资源进行分析,不难发现,一个共同的原因是算法的不清晰。算法作为计算教学的一个核心目标,理应受到重视。而算法的得出,需要学生经历一个不断修正和完善的过程,是学生主动建构的过程。而上述资源①到资源②正是这样一个学生慢慢积淀、体验和感悟的过程。对于资源①②,显然资源②相对资源①更接近乘法的结构。因为资源②反映学生的思维是:3×8=24。虽然学生书面表达是三个0.8相加,但头脑里是依据3×8=24得出2.4的。而这个想法正是引导学生体悟本课算法(转化成整数相乘)的一个有利资源。对于资源③和资源④,哪种更合理,显然是资源④,因为从算法讲,我们算的是8×3,所以3应和0.8中的8对齐。关于资源⑤显然表明学生还没有掌握“小数乘整数”的算法,否则计算过程中间就不会有小数点出现。
(三)对策
对于资源①②,可以让学生比较一下哪种更好,为什么?学生会体会到资源②比较好,学生的理由是“一下子算出来,简单”。这其实就是对整数乘法的一种感悟和体验,只不过是一种感性的而不是理性的,需要进一步去体验。
对于资源③④,可以追问“到底3和谁对齐,为什么?”让学生在追问中去反观自己的想法,这是一种元认知能力,即对自己思维的思维。通过这种追问,让学生监控自己的想法,并判断其合理性与否。不合理的,进而不断调整、修正;合理的,进一步将模糊的直觉提升到清晰的合理性思维,为理解算法作铺垫。当学生能体悟到自己算的是“8×3”亦就达到追问的目标了。
对于资源⑤,可以首先出一些整数乘法,例如“46×13”等,让其竖式计算,然后在竖式上直接改写成小数乘整数,让学生在改的过程中体验“小数乘整数”与整数乘法的关系,进而体悟到“小数乘整数”只需两步:第一步是当作整数乘法算出积;第二步是在积里点小数点。
二、基于算理的分析
(一)典型资源
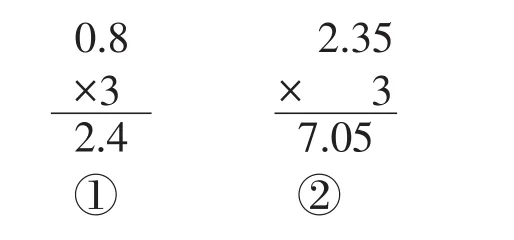
(二)原因分析
到这个环节老师一般都是问“积的小数点”位置怎么确定。对于积的小数点位置的确定,其实是算理的外在表现形式。也就是说,如果学生真正理解了“小数乘整数”的算理,他就知道积的小数点怎么点了。而此时学生只是看到了竖式外在的直观形式,总结说“只要将乘数的小数点拖下来就可以了”。对此,一个同事认为学生这样说是正确的,因为用竖式计算“小数乘整数”不管怎样“积的小数点”都是和乘数的小数点对齐的,也就是学生所说的“拖下来”。乍一听,确实有道理,但稍加分析,其实不然.道理很简单,接下来学习小数乘小数呢,有两个小数点特别是两个乘数的小数点位置不一样的情况,这是积的小数点怎么处理,显然不能像学生说的那样。事实上,“小数乘整数”是“小数乘小数”的基础,亦或说是“小数乘整数”是“小数乘小数”的特殊例子,其本质是一样的,那么积的小数点也应该具有一致性。这样分析,“积的小数点位置”就是算理的直观表达,也就是说学生应该想到:这里的24是24个0.1即2.4;这里的705是705个0.01即7.05。这样结合算理来确定积里小数点的位置才是学生需要认识到的。只不过在此理解的基础上,我们可以进一步帮助学生总结出方法:乘数有几位小数,积就有几位小数。
(三)策略
为了让学生不被竖式表面的直观性所迷惑,我们可以再让学生用竖式做道题:4.12×30。然后同时出示:
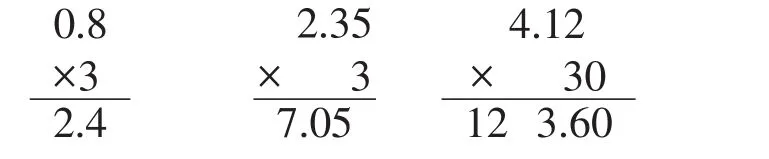
再仔细观察后,问学生:你觉得积的小数点位置应该怎样确定,这样学生就不会说“把乘数的小数点拖下来了”,而是逼着自己进一步寻找合适的理由。此时,我们可以再追问一句:为什么有的积是一位小数,有的积是两位小数。学生不难发现,积的小数位数和乘数的小数位数有关。
学习就是学生自我建构的过程,在这个过程中,学生有着自己的思维、用自己特有的方式去建构,作为教师,我们需要的是读懂学生,遵循学生的思维,顺着学生的思维去引导、启发。

