基于最大相关熵的噪声主动控制研究

翟克宁

（东风柳州汽车有限公司，广西 柳州 545005）

0 引言

噪声主动控制技术在很多方面都得到了广泛的应用，主动降噪系统可以有效地降低被动降噪方法无法解决的低频噪声[1]。

当系统出现脉冲噪声的时候，基于Fxlms（Filter-x least mean square）算法的主动降噪系统会变得不稳定。为了解决脉冲噪声，许多算法已经被提出来[2]。在1995，年Leahy提出的 FxLMP（filter-x least mean p-power）算法，该算法以误差信号P次方最小化代替最小误差信号均方值为目标函数。后来，Wu et al.提出了以误差信号对数值最小为目标函数的对数主动降噪算法Fxloglms（Filter-x logarithmic error lms）[3]。 在 2012 年，George 基于神经网络算法进行鲁棒性设计，提出了 RFslms（Robust filter-x lms）算法[4]。2017年，Lu et al.基于最大相关熵MCC提出了FxRMC算法能有效地降低脉冲噪声信号，但是该算法存在计算复杂度过大问题[5]。

最大相关熵MCC能很好地描述两个随机变量之间的关系[6]。在主动降噪系统中，MCC用来描述初始信号和滤波器产生的期望信号之间的关系。基于主动降噪基本原理，当两个随机信号相似度大时候，系统能有效地较低噪声信号。本文，基于最大相关熵MCC提出了一种变步长FxnMCC算法。该算法能有效地降低脉冲噪声，但是算法的收敛速度远不如FxRMC算法。因此本文进一步提出了混合H-Fx-RMC算法。该混合算法结合了FxRMC算法收敛速度快和FxnMCC算法降噪性能好的优点，并且提高了系统的鲁棒性能。本文最后在Matlab平台进行仿真试验，试验结果表明提出的算法能更好地降低脉冲噪声。

1 脉冲噪声

在一些恶劣的环境中，SαS信号或噪声具有显著的尖峰脉冲特性和拖尾特性。SαS稳定分布是非常重要的非高斯分布，能很好地描述这种尖峰脉冲特性以及严重的拖尾特性。稳定分布是一类具有广泛代表性的随机分布模型。它们的概率密度函数没用统一的封闭表达式，但它的特征函数存在统一的形式。其中SαS信号可以表达为：

其中，r=log10[rand（1，L）]，rand（，）是指符合均匀分布的随机数；Φ维度为1×L并且是在范围内的随机数。α的取值范围约束在0到2，当α越小噪声信号的脉冲程度越高，反之亦然。当α=1时候噪声符合柯西分布，当α=2时，噪声符合高斯分布。

2 自适应主动噪声控制模型

2.1 传统FxLMS算法介绍

如图1所示，基于前馈控制系统的主动降噪系统框图。图中，x（n）表示参考噪声信号，通过参考信号拾音器测得；d（n）表示初始噪声信号，表示为目标降噪点处原有噪声信号；p（z）为初级传递函数，它表示初级信号传递途径的传递函数；s（z）表示次级传递函数，用于描述扬声器布放位置到目标降噪点的传递函数；y（n）表示滤波器生成的信号；e（n）表示降噪后的残余噪声信号，其中 e（n）=d（n）-y（n）。

图1 自适应有源前馈控制系统示意图

主动降噪系统的输入信号为参考信号x（n），假设其向量长度为L，则可以表示为：

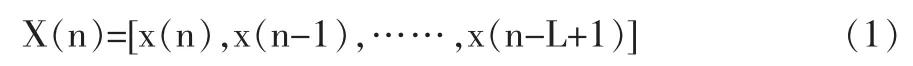
其中，L—输入信号的长度；n—时间索引。另外，滤波器系数向量W（n）可以表示为：

滤波器的输出为y（n），可以表达为：

传统的Fxlms算法以误差信号均方值最小为目标函数，其滤波器系数更新公式表示为：

式中，X'（n）表示参考信号通过次级传递函数估计值（n）。 因此，在时域内，它表示参考信号 x（n）和（n）的卷积：

2.2 FxnMCC算法推导过程

本文算法是基于最大相关熵MCC来提高主动降噪系统的鲁棒性，最大相关熵描述了滤波器生成信号和初级噪声信号之间的关系，以此为目标函数能有效地控制脉冲噪声的衰减。相关熵可以表示为：

其中 E（·）—期望值；Kσ（α，β）—一种高斯内核大小；fα，β（α，β）—α 和 β 的联合分布函数。 α、β—两列随机信号，通常它们的高斯内核Kσ（α，β）定义为：

然而对于离散信号序列来说，两列随机信号的相关熵可以表达为：

以期望信号和输出信号的相关熵作为主动降噪算法的目标函数，利用梯度法来寻求它们相关熵的最大值。因此主动控制算法目标函数为：

根据梯度法原理，滤波器权系数的更新公式为：

目标函数的变化梯度为：

我们令因此FxMCC算法的滤波器权系数的更新方法可以表示为：

滤波器更新的收敛系数μ的值决定自适应过程中系统收敛速度和稳态误差的大小。如果μ的值取值过大，将会导致系统发散不收敛。μ取值过小会导致系统收敛速度慢。一般来说收敛系数的取值取决于滤波器长度和参考信号的功率，归一化版本的FxnMCC算法就是让滤波器收敛系数的值不断地随着参考信号功率更新，其表达式为：

因此，本文提出的FxnMCC算法的滤波器更新系数表达式可以重写为：

2.3 FxRMC算法介绍

FxRMC算法也是以期望信号d（n）和输出信号y（n）的最大相关熵作为目标函数，但是滤波器采用递归形式进行更新。FxRMC算法的主要公式如下：

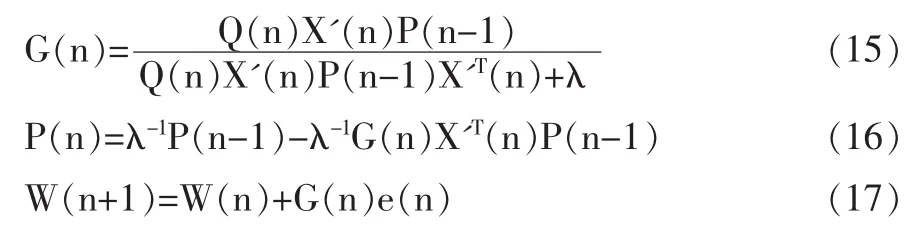
其中 Gp（n）是滤波器增益向量，其维度长度为 1×L；P（n）是输入信号的自相关矩阵的逆，它的维度为L×L；λ代表遗忘因、子λ小于并约等于1。

2.4 混合H-Fx-RMC算法

为了结合两种算法的优点，本文进一步提出了一种混合H-Fx-RMC算法。混合算法先调用FxRMC算法，使残余噪声到达较低的水平，之后再调用变步长FxnMCC算法继续调整滤波器权系数值，达到最优降噪水平。为了决定什么时候转化两种算法，以平均噪声减少量ANR（averaged noise reduction）作为标准定义一个固定的阈值ψ。混合算法一开始采用FxRMC模式更新滤波器权系数W（n），当噪声平均降噪量ANR达到并小于设定的阈值ψ时候，混合算法转化为FxnMCC算法更新滤波器权系数。因此混合算法的关系式可以表示为：

在主动降噪系统中，ANR常用作为衡量算法降噪效果的标准，表达式为：

其中，ξ=0.999，Ae（n）和 Ad（n）分别表示初始信号 d（n）和残余信号e（n）的估计值。阈值ψ的设定一般根据经验为主，根据处理不同环境的噪声进行选择。

3 算法计算复杂度分析

在主动降噪系统实际应用中，为了满足实时性控制，对系统的计算速度有一定的要求。主动降噪算法的计算复杂程度对ANC系统计算速度有着直接的影响，算法的计算复杂度越高，相应地对硬件系统的计算速度要求越快。这也会导致需要高质量硬件部件，增大搭建主动降噪系统的成本，因此如何降低算法的计算复杂度是一个很重要的实际应用问题。

表1 算法计算复杂度对比

如表1所示。显然FxRMC算法的计算复杂度比FxnMCC算法的大很多。混合H-Fx-RMC算法计算复杂度介于两个算法之间。

4 系统仿真与控制实验及结果分析

本文基于MATLAB软件进行编程，仿真对比传统的FxLMS、FxnMCC、FxRMC和 H-Fx-RMC算法处理脉冲噪声的降噪性能。取不同值α的脉冲信号作为仿真参考输入信号。图2呈现了脉冲噪声的时域图，噪声信号体现出尖峰脉冲特性。图2描述了两种情况不同α值的脉冲信号。

4.1 参考信号为脉冲信号试验

参考信号到降噪目标点存在一个初级传递通道，一般来说用初级传递函数Q（z）来描述该通道，我们设置为Q（z）=z-3-0.3z-4+0.2z-5；类似地，主动降噪系统的扬声器发出输出信号，输出信号会经过一段次级通道路径，用次级传递函数描述该通道，可以表示为：S（z）=z-2+0.5z-3；本文仿真算法以ANR作为衡量算法降噪性能的标准，根据ANR定义可知，当ANR的值小于零，系统才有一定的降噪效果，若ANR越小，表明算法降噪能力越强。

图2 脉冲信号时域图，（a）α：=1.1， （b）α：=1.2

本小节试验中以图2脉冲信号作为输入信号。在算法仿真中，高斯内核σ的大小设置为σ2=8，阈值取ψ=-6。FxnMCC算法和H-Fx-RMC算法的迭代步长取μ=0.01，FxRMC算法的遗忘因子取λ=0.95。图3描述的是不同算法降噪的ANR曲线。从仿真结果图可知，传统的FxLMS算法出现发散现象不能衰减脉冲噪声，而本文提出的变步长算法FxnMCC算法和混合H-Fx-RMC算法均能有效地降低脉冲噪声，系统趋于收敛，相比FxLMS算法有更好的鲁棒性。FxnMCC算法解决2500步才趋于收敛，而混合算法和FxRMC算法在1000步以内便接近收敛。证明但是变步长FxnMCC算法相对于FxRMC和混合HFx-RMC算法来说收敛速度慢。而通过第3节的计算复杂度对比我们知道，FxRMC算法计算复杂度比FxnMCC算法高很多，而混合算法在达到设定阈值时候会从计算复杂度高的FxRMC算法转化到计算复杂度低的FxnMCC算法，因此相对FxRMC算法来说计算复杂度肯定是降低的。因此我们可以说混合H-Fx-RMC算法不仅能有效地降低脉冲噪声并且具有收敛速度快计算复杂度较低的良好性能。

图3 试验1不同算法仿真结果ANR曲线，（a）α：=1.1， （b）α：=1.2

4.2 参考信号为脉冲噪声和高斯噪声混合试验

本节试验的参考信号为脉冲噪声和高斯分布噪声想结合，混合类型参考信号噪声如图4所示，混合噪声长度为两万点数，由分别取为前一万点数符合α=2.0的高斯分布噪声，后一万点数为α=1.3的脉冲噪声。图5显示了以混合噪声为参考输入噪声时候，本文提出的算法仍然有良好的降噪效果，传统的FxLMS算法迭代到接近一万多步时候发散，再次验证传统FxLMS算法在脉冲噪声出现时候的性能不住。本文提出的FxnMCC和混合H-Fx-RMC算法能有效地降低脉冲噪声，鲁棒性比FxLMS算法强，得到的其它结论和试验1相似。

图4 混合噪声

图5 试验2不同算法仿真结果ANR曲线

5 结束语

本文进行了脉冲噪声存在时候提高鲁棒性的算法研究。基于最大相关熵MCC，本文提出了变步长FxnMCC算法能很好地降低脉冲噪声，提高主动降噪系统的鲁棒性和降噪性能。但是变步长算法的收敛速度较慢，为了解决这个问题，本文进一步结合现有的FxRMC算法提出了混合HFx-RMC算法。该混合算法的计算复杂度比FxRMC低，具有快速收敛的性能，而且能有效地衰减脉冲信号噪声。本文通过多个仿真研究证明了混合H-Fx-RMC算法的优点。

[1]王登峰，刘学广，刘宗巍，等.基于发动机转速的车内有源消声控制策略和自适应算法[J].公路交通科技，2004，21.

[2]陈克安，马远良.自适应有源噪声控制：原理、算法及实现[M].西北工业大学出版社，1993.

[3]Wu L，He H，Qiu X.An Active Impulsive Noise Control Algorithm With Logarithmic Transformation：IEEE Press；2011.

[4]George NV，Panda G.A robust filtered-s LMS algorithm for nonlinear active noise control.Applied Acoustics，2012，73.

[5]Lu L，Zhao H.Active impulsive noise control using maximum correntropy with adaptive kernel size.Mechanical Systems&Signal Processing，2017，87.

[6]Wu Z，Shi J，Zhang X，Ma W，Chen B.Kernel recursive maximum correntropy.Signal Processing，2015，117.