空调数字化设计分析
唐 军,秦 强
(中国矿业大学,江苏 徐州 221000)
0 引言
随着经济的快速发展,城市中空调的应用更加广泛,为了将市场需求充分满足,就必须迅速有效地设计出性能优越的空调。传统设计方法成本较高、效率低下,无法与现代企业发展要求相适应,故而必须进行空调设计方法的创新。计算机仿真可利用数值实验将实验室实验取代,能将劳动生产率提高、产品开发周期缩短,且成本投入较低,能应用于更多的普通技术人员。
1 冷剂物性的快速计算模型
制冷空调仿真的基础内容中,制冷剂热力性质十分重要,在计算中物性参数的调用次数十分高,计算速度、精度及稳定性会在很大程度上影响装置仿真计算效果。当前,计算制冷剂热力性质的方法有简化拟合关联式法、状态方程法及图表法。本文所提出的计算模型拟合参数偏少、形式简单,计算误差偏小,具有较广的适用范围、曲线稳定性,在系统仿真中的优势十分明显。
1.1 数据拟合范围
以拟合关联式法建立的热物性快速计算模型,对热物性参数数据有着较高的要求。快速计算模型的原始数据采用REFPROP7(美国国家标准计量局开发)导出的数据[1]。考虑仿真实际,仅需拟合饱和线、过热区。过热区范围:过热度1500℃,包和温度-20℃~70℃。 详见图1。
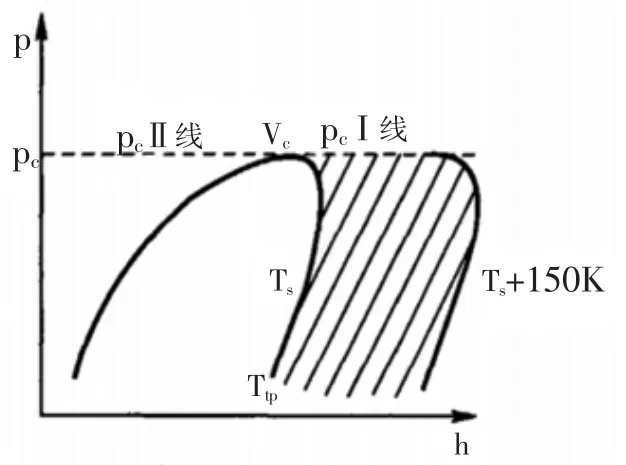
图1 制冷剂的图Fig.1 Diagram of Refrigerant
1.2 数据拟合模型
在一定精度要求下,以往多项式类拟合函数难以对图1的热力性质采用一致拟合函数,针对该缺陷,本文采用下文所述的统一形式的制冷剂过热气体热力性质显式拟合模型,在整个过热区计算范围(0~150K)内,该方程都能取得较高的精度[2]。此外,再加上该方程形式为统一,对分段拟合方法使用中常见的面与面之间不连续的问题也能有效避免。该方程具体如下所示:
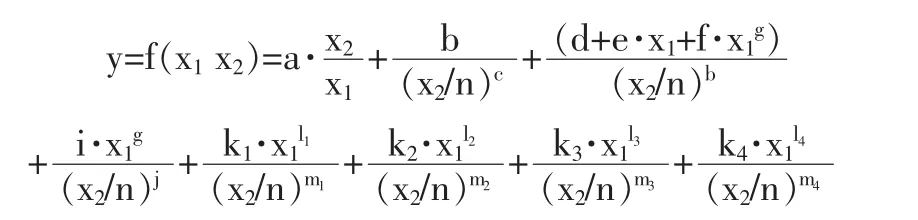
式中,x1,x2—制冷剂在该点的已知物性参数;a~w—方程拟合系数;y—过热区制冷剂的待求物性。将该快速计算模型对比REFPROP7数据源发现,所有快速计算模型总平均偏差不超过0.0769%,最大偏差不超过2.087%,相对于REFPROP7的计算速度而言,高出2~4个数量级。
2 压缩机模型
压缩机性能可对空调系统性能造成极大的影响,变速空调、热泵系统仿真的基础便是合理的压缩机模型。图方法和效率法是目前最常用的常速压缩机建模方法。前者有着更高的相对精度,要求压缩机制造商提供性能数据[3]。然而该方法仅用于少数压缩机中;后者相对更为简单,带实验系数的整体方程使传热传质过程得到了简化。该方法在并未提出较高的压缩机计算精度要求领域中十分适用。
2.1 压缩机性能参数的回归拟合
本文立足于空调系统仿真角度,采用标准的ASHRAE+常数公式形式:
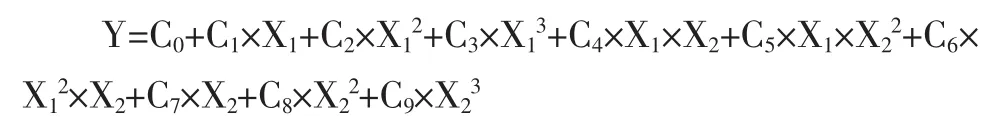
式中:Y—压缩机性能参数,如运行电流、制冷量Q、质量流量、输入功率W等,X1,X2—蒸发温度、冷凝温度。
采用以上数学模型进行拟合,通过对比试验数据发现,平均相对误差达到E-5数量级,最大相对误差达到E-3数量级。
2.2 压缩机性能参数修正
对于上述性能参数拟合结果而言,仅适用于标准工况中,因此在仿真计算过程中需对上述计算过程进行修正。实际系统计算分析中,吸气过热度若是不同于压缩机标定,应以上述拟合方程将标准工况下的压缩机性能计算得出,并以此为根据修正工况质量流量、输入功率。
3 换热器模型
在整个制冷系统仿真中,换热器模型的仿真极其关键,换热器热质交换过程能否有效模拟、换热器两侧传热系数能否准确计算,都会对系统性能模拟计算精确度造成直接影响。对此,在制冷空调仿真领域中始终都将换热器性能仿真、优化设计当作重点研究课题。在实际建模过程中,冷凝器通常被分为液相区、两相区和气相区,而蒸发器通常为过热区、两相区。当前换热器模型主要包含分布参数模型、集中参数模型和分相集中参数模型。
4 毛细管模型
当前,有关绝热毛细管两相流动的研究中,均相平衡模型的应用十分广泛。毛细管有着十分细的管径,故而以一维流动为根据进行考虑,有足够的精度;裸露在空气中的毛细管都可将其当作绝热流动,毛细管出口状态所受到的来自于制冷剂与环境热换量的影响几乎可以忽略不计;而在毛细管内,制冷剂的高速流动会充分混合气液相,气液相之间有着十分接近的流动速度,没有相间速度滑移,工程上可采用均相流(气液相相同流速)进行处理。该模型计算精度十分高。
5 系统仿真模型
在给定环境参数下,通过求解系统循环过程将系统稳定运行工况确定,结合计算机对空调实际运行的制冷量、压缩机功耗、系统性能参数及换热器出风参数进行模拟便是制冷空调系统的仿真计算[4]。系统模型是由各部件模型通过适当的接口参数连接而成。在对系统模型求解时,不但要对各部件模型求解,同时还要对各部件参数之间的耦合关系求解,故而系统模型仿真算法相对于单一部件模型而言更为复杂。此外,通过求解系统模型可将部件模型或算法中的缺陷找出。
部件仿真模型如下:
压缩机模型: (mcom,h1,Mcom,tt,out)=F1(tk,te,th)
冷凝器模型:(mcon,Qc,Mcon)=F2(pc,h1,h2)
毛细管元件模型:(mcap,h3,Mcap)=F3(pc,h2,pe)
以制冷系统某部件模型为头节点,通常情况下都是以压缩机为主,对压缩机流量、输入功率进行计算,并将冷凝器进口参数确定为压缩机出口参数,进而将冷凝器出口参数得出。借助毛细管等焓方程计算蒸发器进口状态,随后分析压缩机流量与毛细管质量流量是否有差异存在,并在完成冷凝温度的调整后,利用蒸发器计算模块计算蒸发器出口流量,最后在调整蒸发器蒸发温度的基础上,实现蒸发器出口制冷剂质量流量与毛细管出口流量的一致,以此进一步稳定系统运行工况,获取制冷量等参数[5]。此外,系统仿真算法不但需对各部件模型求解,同时也提出了求解各部件参数之间耦合关系的要求,系统迭代过程中,因部件模型工况点会产生将所有可能范围覆盖的可能性,故而必定远超现有实验数据范围。而在具体计算中就会有如下问题出现:
(1)输入参数有大范围波动出现时,部分工况点计算无法收敛,进而影响到软件计算的稳定性。
(2)在选取迭代计算初值时若有问题存在,那么最初的迭代会有非正常工况发生,如压缩机模块冷凝温度过高、过热度及蒸发温度偏低等,与压缩机拟合公式适用范围不符合。
随着研究的不断深入,得知上述问题的产生原因主要是迭代参数两分法迭代的上下限值,若
仅是选取一个范围,那么部件模型输入工况参数就会进入某些实际过程中出现几率很小、迭代中却极易进入的区域,如此一来会对迭代过程造成严重影响,甚至会导致迭代计算无法收敛。
要想使软件的稳定性得到提升,就必须不断改进系统算法。而能使计算成功率提升的方法通常有两种,其一是针对系统容量,用户提供一个换热量猜测值,如此一来就能对迭代处置进行设置、刷新,用户若给出了合理的换热量初值,对于迭代过程的收敛能产生一定的帮助。但是,由于无法确定软件面对的用户是否对底层模型建立方法了解,难以给出合理的初值,故而本文通过对迭代上下限区间合理设置的方法实现软件稳定性的提高。具体而言,改进迭代算法的关键在于上下限值是否合适,且该上下限值必须将以下条件满足:
(1)该区间应尽量接近于初值,根据连续迭代法而言,猜测值若接近于真实值,就会拥有更大的收敛机会。
(2)在区间两个端点计算时,与收敛准则相对于的误差必须分别大于、小于零。如此一来就能确保部件输出参数(流量曲线)连续时,无量纲误差的零点始终位于该上下限内,随后采用两分法可将该零点找出。
以上述分析为根据发现,在借助两分法对系统仿真过程中任一循环进行真解探索时,首先应进行基于进退发的模块的设计,以此将迭代的上下限确定,随后以两分法为根据进行搜索,如此以来就可为计算过程中的绝对稳定性提供保障。能够基于物理意义控制计算过程,对于复杂模型的求解非常重要。
6 结论
本文中建立了制冷剂新的快速计算模型、空调系统稳态性能系统仿真模型,进一步将系统快速模拟运行的目的实现,在当前提倡数字化设计、高效率、节能概念的时代中意义十分重大。在系统数值模型的基础上,仿真软件的框架原型采用的是当前使用十分广泛的“设计模式”,实现了完全面向对象方式的空调性能方针、模拟分析软件。制冷空调仿真系统的开发这一过程需要不断进行完善,本文所提出方法能在一定程度上推动制冷空调产品的设计、分析。
[1]庄叔平,谷波,方继华,等.空调箱数字化设计与选型软件平台技术开发[J].流体机械,2015,3.
[2]庄叔平.空调箱数字化设计系统的模型分析[D].上海交通大学,2015.
[3]郝源成.空调箱数字化设计系统的扩展开发[D].上海交通大学,2013.
[4]华宏兵,庄启建.变频技术在空调系统中的应用优势[J].数字化用户,2017,27.
[5]闫晓伟.工业空调节电技术[J].数字化用户,2017,37.

