具有交叉扩散的全寄生药用植物和寄主植物共存问题
胡颖,马云桐,谭启建
寄生植物约有4200多种,在全世界有广泛分布[1],其中的寄生药用植物是中药中的一个特殊类群。已经有很多作者对寄生植物的特殊性、它们与其寄主植物的关系以及生物数学模型进行了研究[1~8]。寄生类型包括全寄生与半寄生。
考虑寄生植物和其寄主植物的扩散模型,寄生植物扩散的密度通量将依赖于寄主植物的密度,即有交叉扩散的现象[9]。依据所考虑的区域,这种扩散有两种类型,即当所考虑的区域只有一种自然条件时,扩散系数、交叉扩散系数和反应函数是连续的,对这类问题和类似的捕食-食饵模型已经有大量文献报导[10~15]。而当所考虑的区域包含不同自然条件时,扩散系数、交叉扩散系数和反应函数都是允许间断的。这种交叉扩散生态模型最近也有数学理论的研究[16]。
我们知道,全寄生植物的导管和筛管分别与寄主植物的导管和筛管相通,从寄主植物上获取自身生活需要的全部营养物质[1]。在自然界中有些药用植物就是全寄生的,比如名贵中药肉苁蓉(Cistanchede serticolaY.C.Ma) 完全寄生于藜科梭梭属植物梭梭(Haloxylon ammodendron(C.A.Mey.)Bunge) 和白梭梭(H.pericum Bunge ex Boiss。)根部[1~2],从这些寄主上获取需要的全部营养物质。而且我们还注意到,肉苁蓉生活在含沙漠和绿洲的这种有不同自然条件的区域。所以本文将重点讨论全寄生药用植物和其寄主植物在一个含不同自然条件区域上共存的条件,为资源可持续利用提供理论依据。
1 数学模型
考虑全寄生药用植物和其寄主植物的两种群交叉扩散模型。第一种植物是寄主植物,它的扩散密度通量与寄生植物无关; 第二种植物是全寄生药用植物,它的扩散密度通量与寄主植物有关,即有交叉扩散现象。
为利用文献[16]的理论结果,本文采用它的记号系统。设Ω是上的一个有界开区域,∂Ω是其边界。Гj( j=1,..., m-1)是一些彼此不相交的曲线,它们把Ω分割成m个子区域Ωi(i=1,..., m)。假设在各子区域上的自然条件允许不同。以ul=ul(x,t)记第l种生物的密度函数,l=1,2。假设在Гj上,密度函数和扩散密度通量是连续的,则满足[16]。

其中,是梯度算子,表函数v在跨过内边界时的跃度,是v的Г法向,是扩散系数,

和都是正常数。分别是寄主植物和寄生药用植物的自扩散系数,它们体现了扩散密度通量受自身密度的影响;而是交叉扩散系数,它体现了寄生药用植物的扩散密度通量受寄主植物密度的影响。问题(1)中的反应函数由下面定义:

其中,都是正常数。在是寄主植物的内禀自然增长率,体现了两种群密度的增加对寄主植物增长率的阻滞作用;在表示如果没有寄主植物时,全寄生药用植物的死亡率,表示寄生药用植物的增长率也是密度制约的,表示寄主植物对寄生药用植物增长率的促进作用。
2 种群的共存条件
要做到资源的可持续利用,就是要使得寄生药用植物和寄主植物共存。在数学上, 就是要利用文献[16]的理论结果, 找出问题(1)正解存在的种群密度条件,这是本文的主要目的,它由下列定理描述:
定理 1.如果下列条件(i) (ii) 满足,则问题(1)存在文[16]中定义2.1意义下的正解u:
(i)对所有且存在使得
(ii) 存在正常数使得
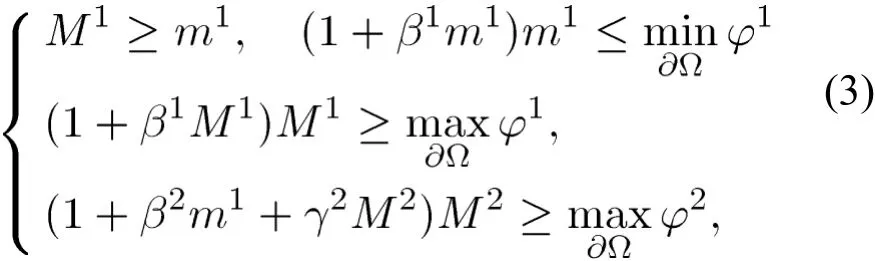
和对所有

其中,

证明:对任意

于是只要记(5)的逆

存在,其中
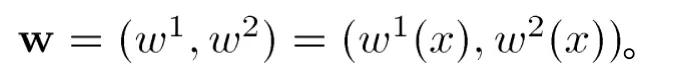
对任意正常数定义

其中从而由[16]知,对任意给定的正常数问题(1)可以被写成等价形式
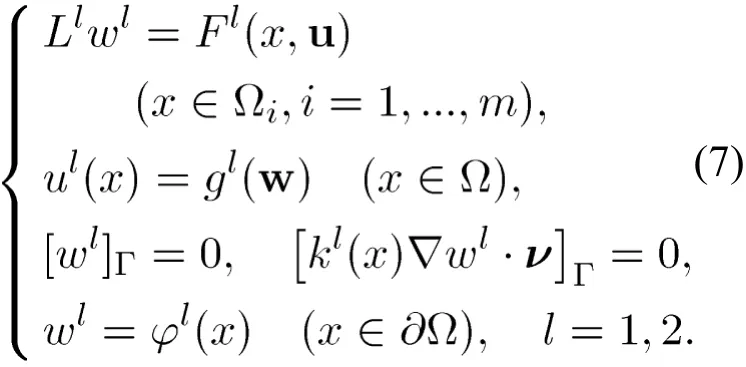
取
从(6)得到

如果
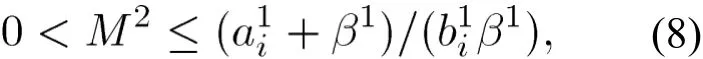
则当时, 对非u1降,对u2非增,而对u1,u2都非降。
根据文[16]中的(3.4)-(3.7)和定理2.1知,如果存在正常数使得对所有

则是(7)在文[16]定义2.2下的耦合弱上下解,且问题(1)有正解满足其中
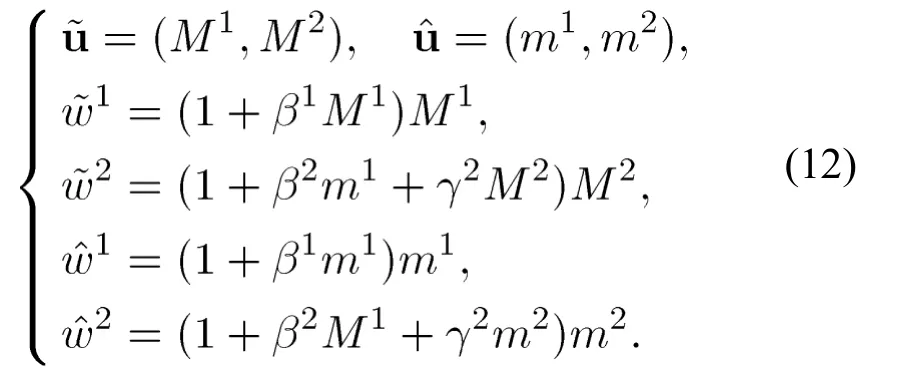
下面找满足上述条件的正常数(10)等价于

我们发现,如果M1,M2和m1满足
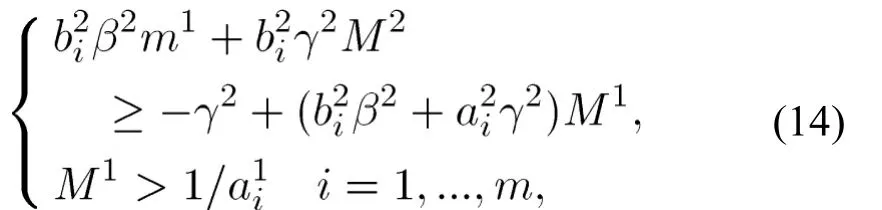
那么对充分小的正数m2,(13)成立,从而(10)成立。
关系(11)等价于
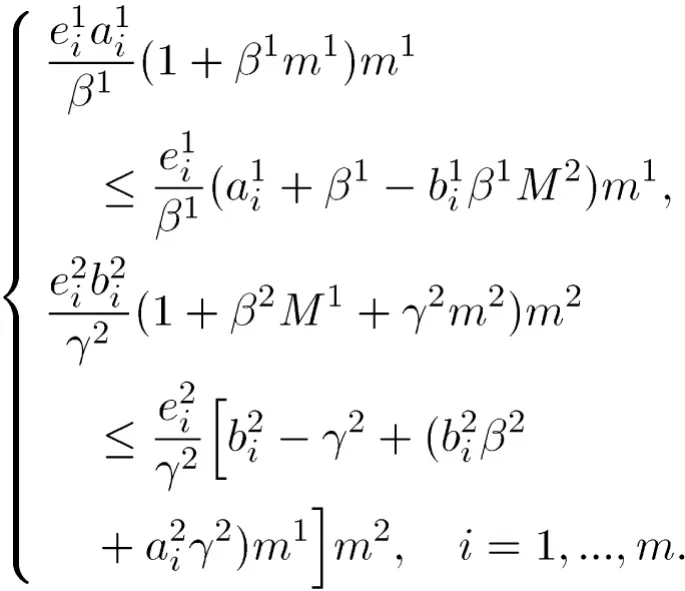
这等价于
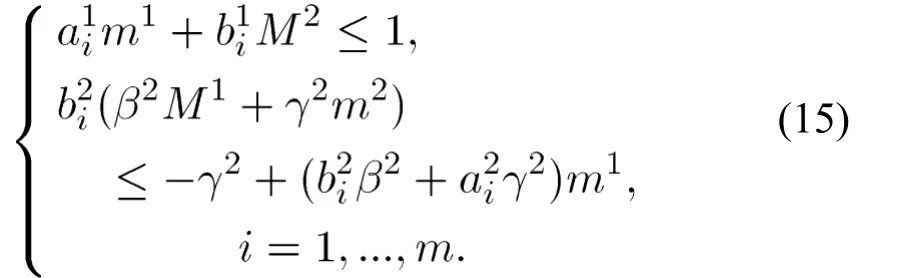
如果M1,M2和m1适合
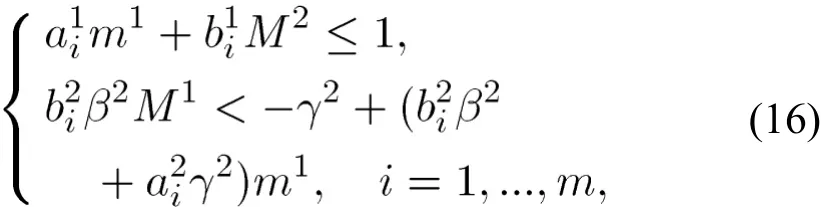
则对充分小的正数m2,(15)得到满足,于是(11)也得到满足。
注意到如果(15)的第一个不等式成立,则从而(8)也成立。所以,综合以上推理,满足(3)和(4)的正常数M1,M2,m1,能够保证对充分小的m2,使得(8),(14)和(16)得到满足。这样(8)-(11)也都得到满足。于是,对充分小的m2是(7)的耦合弱上下解,且问题(1) 存在正解u满足从而,定理1得到了证明。
3 结论与讨论
1)从二种群的共存条件看出,要保证二种群共存,相关量和参数复杂地耦合在一起。我们注意到,要(4)的第一个不等式满足,必须

这意味着寄主植物的密度的最小值必须要大于量
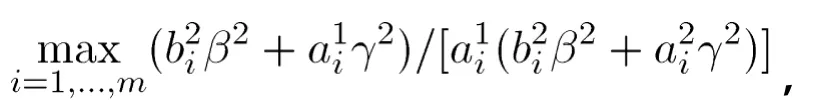
即增大寄主植物的密度。要(4)的第二个不等式满足,必须这意味着寄生药用植物的密度的最大值必须要小于量
即寄生药用植物的密度不能够太大。
由上面的讨论,我们得到结论:增大寄主植物的密度,使得其密度的最小值大于一个与寄生药用植物相关的量; 同时, 控制寄生药用植物密度, 使得其最大值必须要小于一个与寄主植物相关的量。
2)如果区域Ω上只有一种自然条件,则是常值函数,无关,且(1)中不含在Г上的内边界条件。可以从定理1得到相应的共存条件。
[1]盛晋华,张雄杰,刘宏义,等.寄生植物概述[J].生物学通报,2006, 41(3):8-13.
[2]黄勇,骆翔,赵东平,等.全寄生药用植物肉苁蓉微量元素含量分析[J].光谱学与光谱分析, 2010, 30(2):551-553.
[3]屠鹏飞,姜勇,郭玉海,等.肉苁蓉研究及其产业发展[J].中国药学杂志, 2011, 46(12):1882.
[4]黄勇,刘晓萍,骆翔,等.肉苁蓉寄生对梭梭生物量和碳水化合物含量的影响[J].中国农业大学学报,2009, 14 (5):76-79.
[5]郭玉海,崔旭盛,黄勇,等.肉苁蓉寄生对梭梭 N、P、K积累和分配的影响[J].中国药学杂志,2011, 46(14):1062-1065.
[6]Pao C V.Nonlinear Parabolic and Elliptic Equations [M].New York: Plenum Press, 1992.
[7]胡颖,谭启建.沙漠-绿洲区域药用资源的数学模型[J].成都大学学报(自然科学版), 2013, 32(2): 113-120.
[8]胡颖,马云桐,谭启建.寄生类药用及其寄主植物种群的可持续利用[J].中药与临床, 2013, 4(3):1-4.
[9]Shigesada N, Kawasaki K, Teramoto E.Spatial segregation of interacting species[J].J.Theoret.Biol., 1979, 79 (1): 83-99.
[10]Pao C V.Strongly coupled elliptic systems and applications to Lotka-Volterra models with cross-diffusion [J].Nonlinear Anal., 2005, 60 (7):1197- 1217.
[11]Chen X, Qi Y, Wang M.A strongly coupled predatorprey system with non-monotonic functional response [J].Nonlinear Anal., 2007, 67(6):1966-1979.
[12]Li H, Pang Peter Y H, Wang M.Global solutions for a general strongly coupled prey-predator model [J].Appl.Math.Lett.,2009, 22(10): 1508-1512.
[13]李艳玲,李景荣,郭改慧.一类具有交叉扩散的捕食模型非常数正解的存在性[J].应用数学学报,2013, 36(2): 230-242.
[14]刘立昭,李艳玲.一类带交叉扩散项的捕食-食饵模型的共存态.纺织高校基础科学学报, 24(2011): 353.
[15]张航国,容跃堂,张晓晶.一类带有交叉扩散的捕食模型的共存问题[J].纯粹数学与应用数学, 2013,29(4): 403-413.
[16]Tan Q J.An elliptic cross-diffusion system describing twospecies models on a bounded domain with different natural conditions [J].J.Math.Anal.Appl., 2016, 437(2):853-869.

