基于小波KPCA与IQGA-ELM的煤与瓦斯突出预测研究*
徐耀松,邱 微,王治国
(辽宁工程技术大学电气与控制工程学院,辽宁 葫芦岛 125105)
煤与瓦斯突出是煤矿井下含瓦斯煤体在短时间内从煤岩层以极快的速度与强大的冲击力向采掘空间喷出大量瓦斯的一种强烈动力过程,是最严重的瓦斯灾害之一[1-2]。对煤与瓦斯突出强度进行准确预测是煤与瓦斯防治工作的基础,目前针对煤与瓦斯突出预测问题,国内外学者已经研究了很多方法,杨力[3]等耦合了模糊理论和支持向量机算法,建立了基于模糊支持向量机的煤与瓦斯突出预测模型。朱志洁[4]等将主成分分析(PCA)方法应用到BP神经网络中,实现了对煤与瓦斯突出的有效预测。陈全秋[5]等充分结合BP神经网络和遗传算法两种算法的优点,建立了煤与瓦斯突出新的预测方法,该方法预测精度更高。温廷新[6]等利用量子遗传算法(QGA)对最小二乘支持向量机(LSSVM)进行优化,建立了QGA-LSSVM煤与瓦斯突出预测模型。针对煤与瓦斯突出灾害预测,影响因素复杂繁多,各因素之间具有一定的相关性和非线性,且在突出灾害的发生发展过程中多种因素的影响程度各不相同,使得传统的预测方法在预测精度和效率方面难以满足生产需求,还需深入研究致突因素间的相关复杂性及各因素对突出灾害发生的影响程度,以提高突出预测的精度和效率。
因此,本文提出一种基于小波核主成分分析(KPCA)与改进的极限学习机(IQGA-ELM)相结合的预测模型。把小波分析的思想引入到核主成分分析中,先用小波核主成分分析(KPCA)对致突指标进行非线性降维处理,提取其主成分序列,并将提取的主成分序列作为改进量子遗传—极限学习机预测模型的输入,此模型充分利用改进量子遗传算法来优化极限学习机ELM的输入权值和隐含层阈值,极大地提高了ELM模型的预测精度和效率,并通过实例验证、对比分析和实测数据预测分析,证明该模型具有较强的泛化能力。
1 煤与瓦斯突出的致突因素特征提取
1.1 致突因素的选取
煤与瓦斯突出现象是由地应力、瓦斯压力和煤岩物理力学性质等多种因素共同作用产生的[7-8]。在进行煤与瓦斯突出预测时,致突因素的选取影响着整个预测模型的收敛性及准确性[9]。为了准确的评价每个因素,笔者根据煤与瓦斯突出特性相关研究及文献[10],结合突出事故的历史数据,考虑影响因素的易取性和矿区实际情况下,建立了包含地应力P0(MPa)、瓦斯含量Gc(m3/t)、瓦斯压力Pg(MPa)、瓦斯放散初速度V(m/s)、垂深H(m)、地质构造Gs、软分层煤体厚度Hmm、煤的坚固性系数f、煤体破坏类型Dt、煤层原始含水率Wc%、片帮掉渣Cd和瓦斯压力变化Gv共12个致突因素的预测指标系统。由于影响煤与瓦斯突出的因素较多,致突因素间具有复杂的非线性关系,且每种因素对突出事件发生的影响程度均不同,因此选用合适的方法来确定各致突因素对煤与瓦斯突出的影响权重大小十分重要。因此,本文采用核主成分分析方法对预测指标进行降维处理,为了更准确地提取出影响权重较大的几项指标,本文把小波分析的思想引入到KPCA中,将小波核函数当作核主成分分析的核函数来进一步增强KPCA的非线性降维能力。
1.2 小波核主成分分析
核主成分分析(KPCA)是把核函数引入到主成分分析(PCA)中的一种处理非线性问题的一种方法,即通过一个非线性映射函数,将原始低维线性不可分空间中的数据映射到一个高维线性可分空间,并在高维空间中进行主成分分析[11-12]。本文用Morlet母小波核函数来替代传统核函数增强KPCA的非线性降维能力。

h(x)=cos(1.75x)exp(-x2/2)
(1)
设伸缩因子为a,令a∈R;变量x,x′∈Rn,则生成的小波核函数如下所示:
(2)
利用式mλKα=k2α即mλα=kα,在特征空间中求解特征空间上的特征值λi=(λi1,λi2,…,λim)和特征向量ωi=(ωi1,ωi2,…,ωim)。就可得到一组主成分指标Fi为:
Fi=ωi1X1+ωi2X2+…+ωimXm
(3)
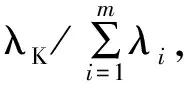
(4)
如果前K个主成分指标的累计贡献率超过一个指定的数值(通常取80%~95%),则可认为求得的K个主成分指标能够充分体现原始预测指标的数据信息。即可写出前K个主成分指标表达式,将K个主成分指标代替原始预测指标进行后续分析。
2 IQGA-ELM预测模型
2.1 极限学习机(ELM)预测模型
极限学习机是一种新型单隐层前馈神经网络,它解决了前馈神经网络学习速度较慢的缺点[13-14]。建立ELM煤与瓦斯突出预测模型时,先将隐含层节点数设为N,训练样本为(xi,ti)∈RN×RM,其中xi=(xi1,xi2,…,xiN)T,ti=(ti1,ti2,…,tiM)T,隐含层的激活函数为G(X),则预测模型表示为:
(5)
式中:βi是第i个隐含层与输出层之间的连接权值,ωi是输入节点到第i个隐层节点的输入权值,bi是第i个隐含层节点的偏差即阈值,h(X)是神经网络隐含层输出矩阵,β是输出层权值。式(5)可简化为:
Hβ=T
(6)
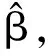
(7)
上述即为对ELM的训练过程,由此可建立ELM预测模型。式中H+为矩阵H的Moore-Penrose广义逆矩阵。
与传统的训练方法相比,ELM神经网络具有学习速度更快,泛化能力更强等优点。因此,把ELM神经网络运用在煤与瓦斯突出预测领域,能够极大地提高突出的预测精度和效率。
2.2 改进量子遗传算法
量子遗传算法(QGA)是量子计算与遗传算法相结合的产物,它实现了比遗传算法更好的效果[15-16]。为提高算法收敛速度和寻优能力,本文对量子旋转门转角的确定进行改进,并融入免疫算法中抗体多样性保持机制和免疫记忆思想以保证种群多样性,得到改进量子遗传算法(IQGA),IQGA算法流程如图1所示。

图1 IQGA算法流程图
在QGA算法中,旋转门转角θi一般通过查表来确定,致使算法收敛速度和寻优效果不理想。因此,本文直接比较当前量子位与最优二进制解来确定旋转门转角。以角度形式考虑旋转门的进化,定义某二进制数角度为:
(8)
旋转角确定公式:
Δθi=(θci-θi)d
(9)
式中:θci为搜索到的最优二进制解第i位的角度,该最优二进制解采用最优保留机制所得二进制解以保证算法的全局收敛性;θi为当前量子染色体第i位所对应角度;d为旋转角调整系数,定义为:
d=(k/N+r)h
(10)
式中:k为种群中第k个个体;N为种群规模;r和h均是常数,r的作用是避免由于种群规模N太大导致d值过小,使旋转角Δθi过小,致使进化速度减慢,h的作用是从整体上调节d值,来控制收敛速度。r和h的取值根据具体情况来设定。该确定方法可使种群中每个个体以不同的速度向最优解进化,进而加快收敛速度,提高算法的寻优能力。
IQGA算法还融合了免疫算法,把适应度函数作为抗原,种群个体作为抗体,则群体个体的期望繁殖概率P的计算公式为:
(11)
式中:λ为概率常数,fv为个体适应度,Cv为抗体浓度。由式(11)可知算法抑制高浓度低适应度的抗体,促进低浓度高适应度的抗体,这一机制保证了种群的多样性。
2.3 IQGA-ELM预测模型的建立
ELM随机产生输入权值和隐含层阈值,使得模型存在泛化能力较差和预测精度不理想的缺点。因此,本文用IQGA算法对ELM的输入权值和隐含层阈值进行优化,进而建立煤与瓦斯突出IQGA-ELM预测模型。
寻优步骤如下:
Step 1 设置种群规模N、记忆库容量M及最大进化代数K等参数。
Step 2 将煤与瓦斯突出ELM预测模型中待优化输入权值和隐含层阈值级联进行量子编码,并初始化量子抗体种群Q(t0)。
Step 4 对各确定解作适应度评价(以均方误差函数作为其适应度函数),记录最优个体,如当前最优个体适应度优于目标值,则以新的最优个体作为下一代进化目标;否则,保持目标值不变。
Step 5 判断是否终止。若所得最优个体为满意解,则终止算法;否则,继续进行。
Step 6 计算P(t)个体繁殖概率P,P值从大到小排序并提取前N个个体,组成父代种群,同时采用精英保留策略更新记忆库。
Step 7 父代群体通过量子旋转门得子代种群。
Step 8 测量子代种群,子代群加入记忆库里的抗体,形成新抗体种群Q(t+1)。
Step 9t=t+1,转至Step 3,直到得到满足条件的最优解,该解即为煤与瓦斯突出ELM预测模型的最优输入层权值和隐含层阈值,由此建立煤与瓦斯突出IQGA-ELM预测模型。
3 预测模型性能及实验结果分析
3.1 基于小波KPCA的特征指标提取
本文从开滦钱家营矿1376综采工作面2016年2月到2016年5月突出事件中随机筛选出200组实测数据作为研究对象,将前160组作为训练样本,后40组作为检验样本,将上述12个变量作为初选预测指标,其中煤体破坏类型共有5类,分别用1~5表示。地质构造分为4类,分别用0~3表示,0、1、2、3分别代表地质构造复杂程度的无、简单、中等和复杂。截取了第191~第200组数据列举如表1所示。
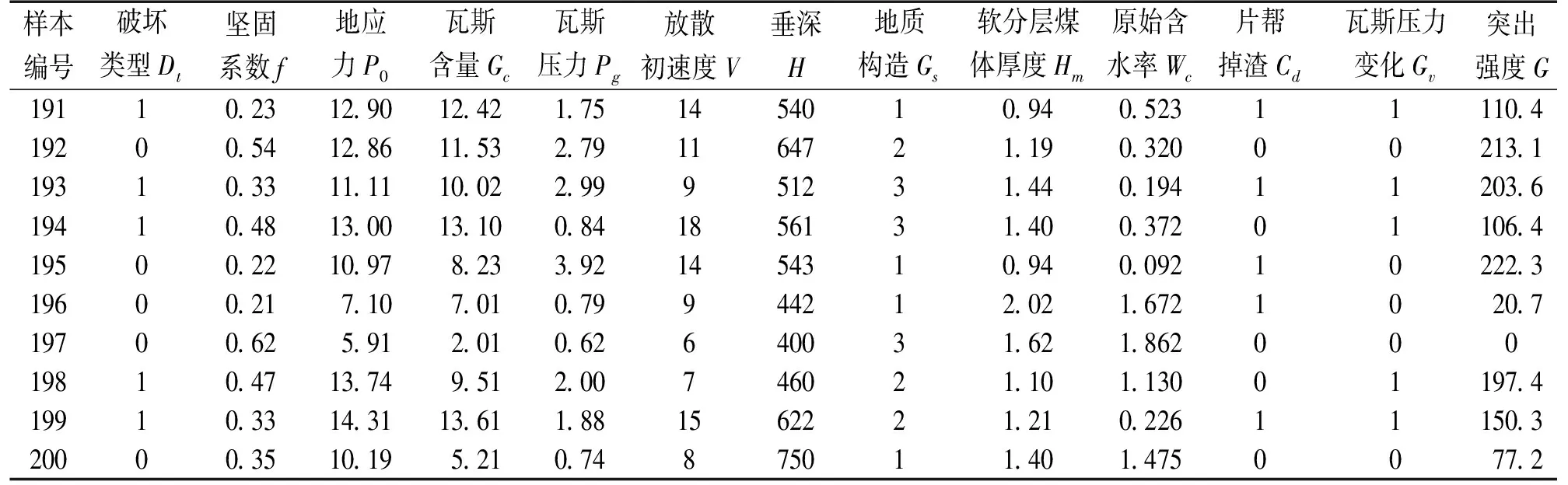
表1 煤矿突出部分数据
先对200组数据进行归一化处理,然后利用小波KPCA对初选预测指标降维,得到的特征值大小及其贡献率如表2所示。根据KPCA的提取原则:主成分累积贡献值必须大于85%。表2中样本集前5项的累计贡献率为86.600%,因此选用前5项主成分指标代替原来的12项初选预测指标,作为建立ELM预测模型的新指标,并计算ELM网络的核矩阵在提取出的特征向量上的投影X1、X2、X3、X4、X5,即可得到降维后的主成分数据,降维后的第191组~第200组数据如表3所示。

表2 各主成分贡献率

表3 降维简化后的部分主成分数据
3.2 训练IQGA-ELM网络性能
利用前160组数据训练ELM网络性能。极限学习机学习性能的优劣取决于隐含层节点数和激励函数的选取。据经验公式,假定煤与瓦斯突出模型的隐含层节点个数为70,在相同网络复杂度下比较各激励函数的泛化性能,如表4所示。

表4 不同激活函数的性能比较
由表4可看出,在相同网络复杂度下Sigmoidal函数与其他激活函数相比,性能较优异,且训练误差较小;在对Sigmoidal函数进行隐含层节点选取时,当L=90时函数训练误差最小并接近平缓,如图2所示。因此,本文中极限学习机的激活函数选取Sigmoidal函数,且隐含层节点个数为90。

图2 隐含层节点的选取
3.3 预测结果分析及实测数据测试
利用前160组数据训练预测模型,设置IQGA算法初始化参数:设N=30,M=30,P=95%,相似度系数为0.7,r=0.01,h=0.1,K=100。按照IQGA算法不断优化ELM的输入层权值及隐含层阈值,其适应度收敛曲线如图3所示。

图3 IQGA-ELM适应度收敛曲线
由图3可看出,算法大约进化到20代全局最佳适应度值收敛且达到最大,从而得到全局最优的ELM模型输入权值和隐含层阈值,进而建立煤与瓦斯突出IQGA-ELM预测模型。
训练模型结束后利用后40组数据进行验证,为了体现该预测模型的优越性,将IQGA-ELM模型与QGA-ELM、ELM、BP模型均对后40组数据进行预测,图4与图5为各模型对后10组数据预测结果和预测相对误差。表5为分别经高斯KPCA和小波KPCA降维后各模型对后5组数据预测的结果。

图4 经小波KPCA处理后各预测模型结果
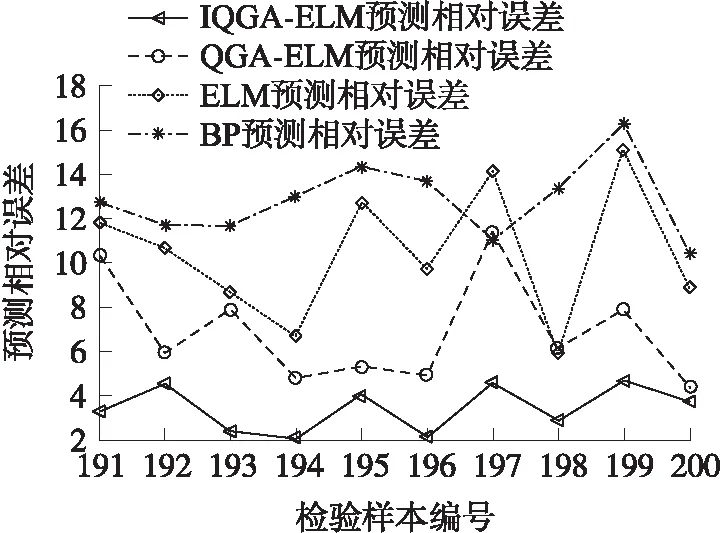
图5 经小波KPCA处理后各模型预测相对误差比较

编号经高斯KPCA处理的预测误差BPELMQGA-ELMIQGA-ELM经小波KPCA处理的预测误差BPELMQGA-ELMIQGA-ELM19615.78212.3739.9327.10913.48210.4387.8234.56319716.00512.2689.7467.21412.99311.0237.9364.78219815.90313.0929.4616.98613.05810.9218.0144.69719914.89212.9789.9947.13512.78211.2137.8954.58920015.73213.1909.7816.87913.72110.8238.8994.742收敛时间/s1.0210.9291.6731.9020.9710.7681.4461.812
由图4和图5可知,在经过小波KPCA处理过的4种预测模型中,IQGA-ELM预测模型的预测值最接近于样本的真实值,而且该模型在每个验证样本上测试所得的预测相对误差均小于其他模型。
从表5中可看出,经小波KPCA处理后各预测模型的收敛时间明显优于经高斯KPCA处理后所花费的时间,且经小波KPCA处理后4种模型的预测误差更小,稳定性更高,特别是IQGA-ELM预测模型表现更为显著。对BP模型和ELM模型而言,后者的运算速度和预测误差均优于前者,QGA-ELM模型虽在一定程度上优化了ELM 模型,但效果仍不理想,IQGA-ELM预测模型的预测误差相对于BP、ELM、QGA-ELM模型有了明显的提高。从收敛时间来看,IQGA-ELM模型耗时较长,但仍处在合理范围内,在煤与瓦斯突出灾害问题上,当收敛时间在合理范围内更加看重预测模型的精确性。因此,经小波KPCA处理后的IQGA-ELM模型预测值最准确,预测精度比BP、ELM、QGA-ELM模型都高,泛化能力最好,能够用来有效预测煤与瓦斯突出强度。
笔者在钱家营矿1376综采工作面的突出数据中截取2015年1月到12月的4800组突出数据进行了实测数据预测分析。将数据按照时间顺序输入到训练好的小波KPCA-IQGA-ELM预测模型中,把这一时间段内模型的预测结果与该矿实际发生的灾害次数和灾害程度进行了比较,结果如表6所示。

表6 钱家营煤矿突出数据预测结果
结果表明,基于小波KPCA和IQGA-ELM预测模型的平均预测相对误差为4.786%,模型的输出值与真实值较接近,平均预测准确率高达95.79%。因此,本文提出的基于小波KPCA和IQGA-ELM预测模型误差小、预测结果准确度高、泛化能力强,可应用于煤与瓦斯突出预测领域,有利于预防煤矿瓦斯突出灾害。
4 结论
①本文把小波分析思想与核主成分分析方法相结合,提出小波核主成分分析方法,提高了核主成分分析的非线性映射能力,准确地提取出煤与瓦斯突出的主成分指标。
②针对传统ELM算法的随机性缺点,将改进量子遗传算法(IQGA)与极限学习机(ELM)进行耦合,提出基于小波KPCA和IQGA-ELM的煤与瓦斯突出预测模型,优化了ELM模型的输入权值和隐含层阈值,显著地提高了模型的预测精度。
③通过实例验证、对比分析以及实测数据预测分析,证明该预测模型的辨识度较高、泛化能力强、具有较高的预测精度,能够应用在煤与瓦斯突出预测领域。
参考文献:
[1] 闫江伟,张小兵,张子敏. 煤与瓦斯突出地质控制机理探讨[J]. 煤炭学报,2013,38(7):1174-1178.
[2] Li Shugang,Zhang Tianjun. Catastrophic Mechanism of Coal and Gas Outbursts and Their Prevention and Control[J]. Mining Science and Technology(China),2010,20(2):209-214.
[3] 杨力,耿纪超,汪克亮. 模糊支持向量机在煤与瓦斯突出预测中的研究[J]. 中国安全生产科学技术,2014,10(4):103-108.
[4] 朱志洁,张宏伟,韩军,等. 基于PCA-BP神经网络的煤与瓦斯突出预测研究[J]. 中国安全科学学报,2013,23(4):45-50.
[5] 陈全秋,郭勇义,吴世跃,等. 遗传算法与神经网络的结合在煤与瓦斯突出危险性预测中的应用研究[J]. 中国煤炭,2010,36(3):86-89.
[6] 温廷新,孙红娟,张波,等. 煤与瓦斯突出预测的QGA-LSSVM模型[J]. 中国安全生产科学技术,2015,11(5):5-12.
[7] 付华,王馨蕊,王志军. 基于PCA和PSO-ELM的煤与瓦斯突出软测量研究[J]. 传感技术学报,2014,27(12):1710-1715.
[8] 谢国民,谢鸿,付华,等. 煤与瓦斯突出预测的NN-SVM模型[J]. 传感技术学报,2016,29(5):732-738.
[9] 付华,李海霞,卢万杰,等. 一种改进的极限学习机煤与瓦斯突出预测模型[J]. 传感技术学报,2016,29(1):69-74.
[10] 周垒. 浅析开滦钱家营矿地质类型划分[J]. 水力采煤与管道运输,2015(1):65-68.
[11] Zyad Elkhadir,Khalid Chougdali,Mohammed Benattou. Intrusion Detection System Using PCA and Kernel PCA Methods[M]. Springer International Publishing:2016:13-22.
[12] 迟恩楠,李春祥. 基于优化组合核和Morlet小波核的LSSVM脉动风速预测方法[J]. 振动与冲击,2016,35(18):52-57.
[13] Xin Yuanfang,Jiang Yuanyuan,Zhang Xuemei. Gas Outburst Prediction Model Based on Empirical Mode Decomposition and Extreme Learning Machine[J]. Recent Advances in Electrical and Amp;Electronic Engineering,2015,8(1):50-56.
[14] Deng Chenwei,Huang Guangbin,Xu Jia,et al. Extreme Learning Machines:New Trends and Applications[J]. Science China(Information Sciences),2015,58(02):5-20.
[15] 王涛,王洋洋,郭长娜,等. QGA-RBF神经网络在矿井瓦斯涌出量预测中的应用[J]. 传感技术学报,2012,25(1):119-123.
[16] 张立仿,张喜平. 量子遗传算法优化BP神经网络的网络流量预测[J]. 计算机工程与科学,2016,38(1):114-119.

