一种基片式光纤光栅应变增敏传感器*

谭跃刚,陈宜炀,李瑞亚,毛 健

(武汉理工大学机电工程学院,武汉 430000)

将裸光纤光栅直接粘贴于待测体表面,利用光纤光栅对应变敏感的特性直接进行应变测量是目前最为常见的方法;然而在实际应用中由于光纤光栅的涂覆层、粘接剂弹性模量与粘弹性、粘贴的工艺等因素影响,其应变灵敏度将十分不稳定[8-11]。为了提高光纤光栅传感器的稳定性与灵敏度,产生了多种光纤光栅传感器封装技术。Litong LI等[12]提出了一种管式封装的光纤光栅应变增敏方法,通过管结构两边固定以及管结构的变直径设计形成增敏结构;应用该理论设计了一种应变传感器,其应变灵敏度为2.52 pm/με,并将其应用于公路桥上的长期结构健康监测。梁磊[13]等提出了一种圆环基片式FBG应变传感器,通过设计圆环结构的基片实现了温度补偿,并获得了较高的灵敏度(3.766 pm/με)。王坤[14]等基于法布里-珀罗干涉仪和光纤布拉格光栅原理设计了一种双参量光纤传感器分别达到了8.63 pm/με与1.11 pm/με的应变灵敏度和-1.60 pm/℃与9.75 pm/℃的温度灵敏度;实现了对温度与应变的同时测量。Jiangbing Du[15]等利用基于四波混频的频率啁啾放大技术在不对FBG进行增敏封装的情况下直接实现了13.3 pm/με的应变灵敏度。

上述提到的几类光纤光栅应变传感器中,灵敏度有高有低,比如管式封装与基片式封装虽然稳定性好,但灵敏度较低,且结构复杂;而后两者的在传感器原理与解调技术上进行了改进与创新,获得了较高的灵敏度,但难以直接应用于工程实际中;目前对大型机械装备的应变检测而言,由于其具有总体变形大,应变小,低频振动的特点,急需灵敏度与测量精度高,一致性与稳定性好的应变传感器。因此本文提出了一种光纤光栅应变增敏传感器,利用杠杆原理有效的提高了光纤光栅对应变测量的灵敏度,同时通过基片封装的方式提高了其稳定性。

1 应变增敏原理与传感模型

如图1所示,该光纤光栅应变增敏传感器通过对封装基片的杠杆结构设计,大大提高提升光纤光栅基片式应变传感器的灵敏度;该传感器主要包含以下几个部分:弹性杠杆增敏基片,光纤光栅以及传感器附件;弹性增敏基片包含有左右固定平板与杠杆增敏机构,同时设计圆角避免应力集中对应变增敏效果的影响。传感器封装过程中需要在施加预紧力的情况下利用粘接剂将光纤光栅粘贴固定于该基片上,避免该传感器受到压缩应变时光纤光栅弯曲无法感知应变变化;其使用方法为将左右固定平板通过粘接剂直接固定于待测基体上,对待测基体的应变进行检测。

图1 光纤光栅应变增敏传感器

图2(a)为固定后的FBG传感器简化所得的传感模型,其中左右固定平板与待测结构完全固定;将基片内部各结构简化为杆结构,考虑光纤光栅在轴向具有一定的刚度,且仅能拉伸与压缩,因此将其简化为绳结构。当传感器工作时,点A产生了水平方向的变形Δl,此时在该简化模型中各杆仅受拉压与弯曲作用,可以认为该传感结构为超静定结构;以AG两点作为静定基对该结构进行受力分析,其中CG为光纤光栅。将点A与点G的约束解除如图2(b)所示,小变形假设情况下,纵向上的支反力与弯矩很小可以略去,因此简化为二次超静定结构;解除约束后得到的相当系统,此时点A与点G受到水平方向的力X1与X2。

图2 FBG增敏传感器应变传感模型

根据变形协调条件与叠加原理对该结构的变形Δl与X1、X2之间的关系进行分析,设X1、X2为单位力;当X1单独作用在增敏结构上时,在静定基A点与G点上产生变形为δ11与δ21;同理,当X2单独作用在增敏结构上时,A点与G点上产生的变形为δ12与δ22。可得:

(1)

利用莫尔积分对δ11、δ12、δ21、δ22进行计算,由位移互等定理可得δ12=δ21,因此只需要求取δ11、δ12与δ22可得:

(2)

将表1中各参数代入式子(2)中求取δ11、δ12、δ21、δ22。将求得4个参数代入式子(1)中求解X1,X2:

②矿业废弃地一般存在大量石块或风化的大颗粒碎石，整体上粒径较大，容易透水，而底泥则粒径细小，紧实度高，用于矿业废弃地改良可以实现物理结构互补，提升废弃地的保水蓄水能力，满足植物生长需求。

X1=1.510 1ΔlX2=0.219 7Δl>

(3)

杆CG光纤光栅变形大小为:

(4)

因此基体产生大小为Δl的变形时该增敏基片上的光纤光栅所受应变与基体的应变关系为:

(5)

即其增敏倍数P=5.7648。根据光纤光栅仅受轴向拉力情况下应变与波长的关系可得光纤光栅的波长变化为:

Δλ=λ(1-Pe)Δε=KΔε

(6)

取Pe=0.22,λ=1 550 nm时,可得裸光栅的应变灵敏度K为1.209 pm/με,与增敏倍数P相乘可得该光纤光栅应变增敏传感器的理论灵敏度为6.970 pm/με,可知其应变增敏效果远大于一般的光纤光栅应变传感器。

图3 增敏传感器与裸光栅有限元分析

3 仿真分析

为了分析该应变传感器增敏效果是否符合理论计算,通过ANSYS Workbench进行FEM分析并与理论计算结果进行对比。如图3(a)所示,将应变增敏传感器粘贴于等强度悬臂梁上进行标定实验,将悬臂梁模型导入ANSYS中进行实际实验的仿真;固定悬臂梁一端,另一端在砝码盘上加载不同载荷对直接粘贴的光纤光栅与应变增敏传感器的应变感知能力进行考察。应变增敏传感器与裸光纤光栅根据实际粘贴方式固定于该标准悬臂梁上,由于裸光栅在实际粘贴过程中通过有机胶水进行覆盖,因此设计一个30 mm×5 mm×1.5 mm的方形胶体对其进行模拟。

将整体结构导入ANSYS Workbench并设置相应边界条件与材料属性,设置加载步长为10 N,终止载荷为80 N并进行计算;同时通过MATLAB对上文中的理论结果在拉伸件上的应变大小进行数值计算。有限元仿真的各项材料属性如表2所示。

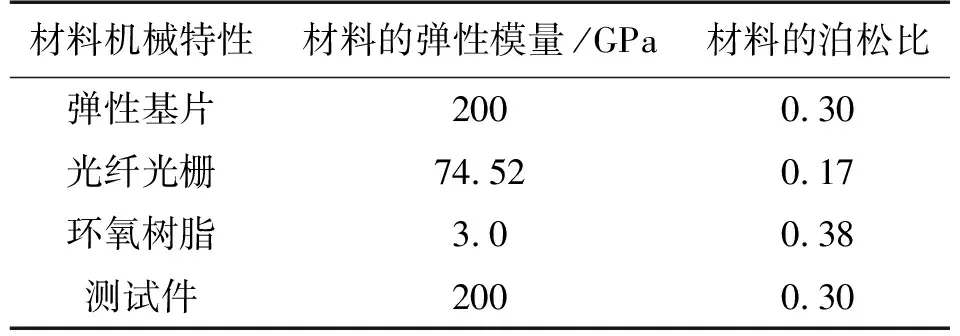
表2 有限元仿真各项材料属性

如图3(b)所示,应变增敏基片的理论计算值与有限元仿真值线性度均十分良好,对比直接粘贴的裸光纤光栅所感知的应变而言均有较大的增敏效果,同时对比增敏基片理论计算值与有限元仿真值,可以看出理论计算值的应变值大于有限元仿真得出的结果。考虑到悬臂梁的厚度为8 mm,而应变增敏传感器的厚度为1 mm因此其上的光纤光栅距离中性层为5 mm,与裸光栅直接粘贴的方式相比距悬臂梁的中性层增大了1 mm,因此相较于悬臂梁表面而言,由于中性层的变化,应变增敏传感器自身厚度导致了其测量结果增加了25%。为了对比在相同情况下应变增敏传感器与裸光栅之间的增敏关系,对结果进行处理,可得理论计算与仿真所得的增敏倍数分别为5.764 8与5.468 3,差值百分比为5.143 3%,因此应变增敏传感器的应变灵敏度根据光纤光栅的应变计算公式推算可得6.611 pm/με。造成两者差别的主要原因为应变增敏传感器的理论计算模型中,使用了多种简化方法:如将杠杆增敏结构简化为简单杆模型,并且在计算过程中以杆的中心作为各个参数值的中心点,并且在实际设计结构的时候为了避免应力集中,采用了圆角设计,影响了有限元仿真中的应变检测结果。

4 传感特性实验

4.1 静态特性实验

在进行实验前需对设计的传感器进行封装与安装;传感器封装所选用的粘接剂为EPO-TEK 公司生产的双组份高温热固型环氧树脂353ND,该粘接剂常用于光纤类产品的粘接,具有优异的温度特性,能长期工作于200 ℃,且其玻璃化转变温度大于90 ℃,即在90 ℃以下其粘接特性基本保持不变。

传感器封装与安装过程:

(1)粘接剂的预制:取用353ND的AB两种胶水以10∶1的比例进行精确称重并进行混合。

(2)弹性基片的预处理:对传感器弹性基片的封装表面进行打磨、清洁并在光纤放置位置划线;将弹性基片置于可调加热台上,位置微调后进行固定,设置加热台的预热温度为70 ℃。

(3)光纤光栅的固定与预应力施加:取出光纤光栅,去掉过长尾纤,将其一端利用设计的磁铁固定座固定,在光纤另一端悬挂合适重量的砝码进行重力预紧,微调加热台位置确保光栅栅区位置准确位于弹性基片划线位置中间。

(4)利用牙签挑起少许混合胶液涂覆于弹性基片光栅固定位置,根据353ND的说明可知该粘接剂固化时间随温度变化而变化,在120 ℃时其固化时间仅需5 min;等待涂覆的混合透明胶液完全变为褐色后,进行分步降温,避免由于353ND与弹性基片之间由于热膨胀系数差别过大,在快速降温过程中出现粘接剂脱落现象;降至室温后,取下砝码,解除光栅与弹性基片的固定,完成传感器的封装。

图4所示为静态特性实验原理与实验过程图,将应变增敏传感器粘贴于等强度悬臂梁上,同时在该悬臂梁上粘贴有裸光纤光栅作为对比;在悬臂梁一端加载/卸载砝码进行标定实验。由解调精度为1 pm的光纤光栅解调仪(高思光电OPM800)对裸光纤光栅与应变增敏传感器进行中心波长变化的监测。在实验过程中由0 N加载至78.4 N,步长为9.8 N,每次加载完毕后稳定1 min,加载至78.4 N后以同样步长由78.4 N卸载到0 N。

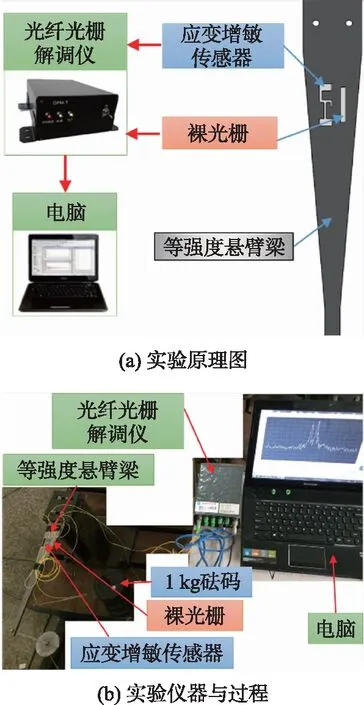
图4 悬臂梁实验配置

对悬臂梁进行的一次加载卸载实验,结果如图5所示,横坐标为加载力,纵坐标为应变增敏传感器与裸光栅的中心波长漂移值,整体呈现良好的线性度。

图5 加载卸载后光纤光栅波长变化

图6(a)为对光纤光栅进行3次加载卸载实验取平均的结果,通过对实验结果的拟合可得应变增敏传感器的灵敏度是裸光栅的6.33倍,且具有良好的线性度,其拟合度为0.999 98。考虑到传感器厚度可得实际增敏倍数为5.064倍。取三次重复实验结果进行分析,可得应变增敏传感器在三次实验的灵敏度增敏倍数分别为5.088、5.068、5.037,与平均值相比其重复性误差分别为0.47%、0.07%和-0.53%;可以认为该传感器具有良好的重复性。根据光纤光栅的轴向应变模型可知该应变增敏传感器的灵敏度为6.122 pm/με,与理论计算值(6.970 pm/με)以及仿真结果(6.611 pm/με)有一定的差距(13.9%与7.99%),其主要的原因是粘接剂(环氧树脂)的低弹性模量以及光纤光栅与基体之间的粘接厚度导致的应变传递效果降低,同时由于应变增敏传感器除了与拉伸件固定的时候使用了粘接剂,在封装光纤光栅的过程中同样使用了粘接剂,因此造成了应变传递效果的进一步下降。

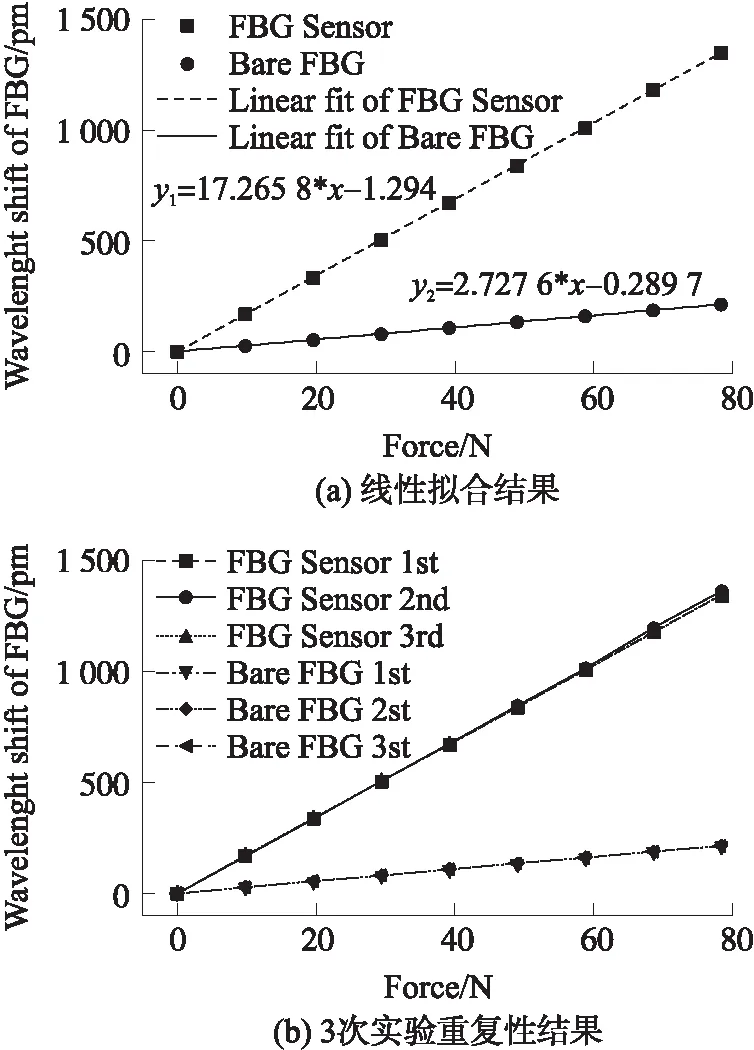
图6 应变增敏传感器重复性与线性度

4.2 动态特性实验

为了研究该应变增敏传感器对动态应变的检测能力,对该等强度悬臂梁进行动态激振实验,实验原理如图7所示。通过激振器进行不同频率下的激振实验。实验配置包括如下:悬臂梁固定平台、激振器、高速光纤光栅解调仪(采样率2 kHz)、以及信号发生器与信号功率放大器。信号发生器产生正弦信号,并通过功率放大器将信号放大传输至激振器产生激振;由高速光纤光栅解调仪获取光纤光栅应变传感器以及直接粘贴的裸光栅的中心波长变化的信号。

图7 动态特性实验原理与配置

图8 裸光栅与FBG传感器1 Hz～200 Hz扫频响应特性

对悬臂梁施加1 Hz～200 Hz的扫频信号,时域信号如图8(a)所示,可以明显看出光纤光栅增敏传感器在不同的频率下具有明显的增敏效果,且具有良好的频率跟踪特性。对信号进行傅立叶变换,获取的时域特性曲线如图8(b)所示,该光纤光栅传感器在时域响应上与裸光栅一致;由于悬臂梁刚度较大,而激振器的功率较低,因此在100 Hz以上时,悬臂梁受到的激振力较小,裸光栅测得的信号小于随机噪声,无法进行进一步的对比。

为了进一步分析增敏传感器的动态响应,以 5 Hz 为步长,进行5 Hz～100 Hz的激振频率下光纤光栅增敏传感器与裸光栅响应对比实验。对不同激振频率下的实验数据进行傅立叶变换,并求取该增敏传感器与裸光栅的比值,获取在5 Hz～100 Hz内应变增敏倍数的变化,结果如图9所示,可知该光纤光栅应变传感器在0～100 Hz内有着良好的动态响应特性,能够保持一定的增敏倍数,在1 Hz～100 Hz内应变增敏传感器的平均增敏倍数为5.069,与静态悬臂梁实验结果进行对比,最大误差为2.34%,最小误差为0.006 7%,平均误差为0.12%。

图9 应变增敏系数在5 Hz～100 Hz内的变化

5 结论

本文针对传统光纤光栅应变传感器应变灵敏度小的缺陷,提出了基于杠杆原理的增敏结构,并设计了相应的光纤光栅应变增敏传感器。理论分析了该应变增敏传感器的应变传感模型,并计算出了在该尺寸下该传感器的应变灵敏度为6.970 pm/με,通过有限元对该传感模型进行验证,计算的应变灵敏度为6.611 pm/με。通过悬臂梁标定实验对该传感器进行灵敏度标定,实验结果表明其灵敏度为6.122 pm/με,在实验中与直接粘贴裸光栅直接测量应变的方法相比,该传感器在实验过程中展现了良好的静态特性,并且其实际增敏倍数达到了5.064,线性度达到了0.999 98。通过悬臂梁振动激励实验,对该传感器的动态特性进行研究,实验结果表明,在0～100 Hz范围内,其应变增敏倍数具有良好的一致性,平均增敏倍数为5.069。因此该光纤光栅应变增敏传感器能够有效的提高应变检测灵敏度,可以应用于大型机械装备的小应变检测,同时由于其高灵敏度,对应变的检测精度也具有很大的提升。

参考文献:

[1] 丁梓涵,赵其华,彭社琴,等. 光纤和电阻应变片在结构变形测试中的对比试验研究[J]. 传感技术学报,2015,28(8):1149-1154.

[2] Hearn G,Testa R B.Modal Analysis for Damage Detection in Structures[J]. Journal of Structural Engineering,1991,117(10):3042-3063.

[3] 周祖德,谭跃刚,刘明尧,等. 机械系统光纤光栅分布动态监测与诊断的现状与发展[J]. 机械工程学报,2013,49(19):55-69.

[4] Zhou Z D,Liu Q,Ai Q S,et al. Intelligent Monitoring and Diagnosis for Modern Mechanical Equipment Based on the Integration of Embedded Technology and FBGS Technology[J]. Measurement,2011,44(9):1499-1511.

[5] Lopez-Higuera J M,Cobo L R,Incera A Q,et al. Fiber Optic Sensors in Structural Health Monitoring[J]. Journal of Lightwave Technology,2011,29(4):587-608.

[6] Guo H,Xiao G,Nezih M,et al. Fiber Optic Sensors for Structural Health Monitoring of Air Platforms[J]. Sensors,2011,11(4):3687-705.

[7] Li H N,Li D S,Song G B.Recent Applications of Fiber Optic Sensors to Health Monitoring in Civil Engineering[J]. Steel Construction,2008,26(11):1647-1657.

[8] 王花平,周智,刘婉秋,等. 柔性基体材料封装FBG传感器的应变传递误差分析[J]. 传感技术学报,2015,28(4):492-497.

[9] 李红,祝连庆,刘锋,等. 裸光纤光栅表贴结构应变传递分析与实验研究[J]. 仪器仪表学报,2014,35(8):1744-1750.

[10] Zhang W,Chen W,Shu Y,et al. Effects of Bonding Layer on the Available Strain Measuring Range of Fiber Bragg Gratings[J]. Applied Optics,2014,53(5):885-891.

[11] 刘明尧,季冬亮,肖爽,等. 胶黏剂黏弹性对粘贴式FBG应变传递的影响[J]. 光学精密工程,2016,24(6):1307-1318.

[12] Li L,Zhang D,Liu H,et al. Design of an Enhanced Sensitivity FBG Strain Sensor and Application in Highway Bridge Engineering[J]. Photonic Sensors,2014,4(2):162-167.

[13] 梁磊,曹珊,仇磊,等. 一种温度自补偿的高灵敏度光纤光栅应变传感器[J]. 光电子·激光,2017,28(7):695-699.

[14] 王坤,俞本立. 基于法布里-珀罗干涉仪和光纤布拉格光栅的双参量光纤传感器[J]. 量子电子学报,2016,33(5):604-609.

[15] Du J,Li L,Fan X,et al. Sensitivity Enhancement for Fiber Bragg Grating Sensors by Four Wave Mixing[J]. Photonics,2015,2(2):426-439.

谭跃刚(1959-),男,分别于1983年和1989年在重庆大学获得学士与硕士学位,2005年于武汉理工大学获得博士学位,现为武汉理工大学机电工程学院教授、博士生导师,主要研究方向为机械故障诊断和机器人技术,ygtan@whut.edu.com;