基于小波分析的MEMS加速度计去噪优化算法*
李世银,张 楠,武中文,王洪梅
(中国矿业大学信息与控制工程学院,江苏 徐州 221000)
惯性导航技术是目前一个重要的研究课题,惯导技术成本低、短时精度高[1]、且不受外部环境的限制,适用于矿井、密林和室内等复杂环境中,因此,在军事、航空和个人导航方面得到了广泛的应用[2-3]。MEMS加速度计是常见的惯性导航器件,多用于行人姿态检测和位移估算[4]。而受自身工艺条件的影响,加速度计输出信号普遍存在量化噪声、速度随机游走和零偏不稳定性等误差,其产生的累积误差将直接影响导航精度,因此,有必要对加速度计噪声进行辨别和消除。
在信号去噪的研究中,需对噪声进行分析和建模,Allan方差是一种时域分析技术,在分析随机误差方面占据显著优势,因此,近年来学者多采用Allan方差对惯性传感器进行误差分析[5-6]。为了克服传统的建模方式复杂度高且参数选取困难等问题[7],针对MEMS加速度计随机噪声长相关、非平稳等特性,许多学者提出了基于小波分析的阈值降噪方法,并在阈值函数的构造方面做了大量的研究。为了解决传统软、硬阈值函数存在固定偏差和不连续的问题,陆续有学者提出了改进的阈值函数,包括半软阈值函数[8]、渐进半软阈值函数[9]、Xing阈值函数[10]、遗传自适应阈值函数[11]等,取得了较好的去噪效果,但这些阈值函数在各尺度上处理方式单一,适应性差。本文首先利用Allan方差分析MEMS加速度计信号的随机噪声类型,构造噪声模型,随后在此基础上提出了一种基于小波分析的多尺度阈值去噪方法,并将其应用于惯导系统中,从而提高系统导航精度。
1 MEMS加速度计噪声分析及建模
1.1 MEMS加速度计噪声分析
MPU-9250是InvenSense公司生产的第2代9轴运动传感器,集成了三轴的MEMS加速度计、陀螺仪和磁力计,因其集成度高、成本低得到了广泛的应用。本文选用MPU-9250采集加速度计数据,在 25 ℃恒温条件下预热30 min,将其静置于水平桌面上,采样频率为50 Hz,对其持续采样2 h,并对采样数据进行Allan方差分析,σ(T)-T(标准差-相关时间)双对数曲线和主要误差项系数如图1、表1所示。

图1 Allan方差双对数曲线
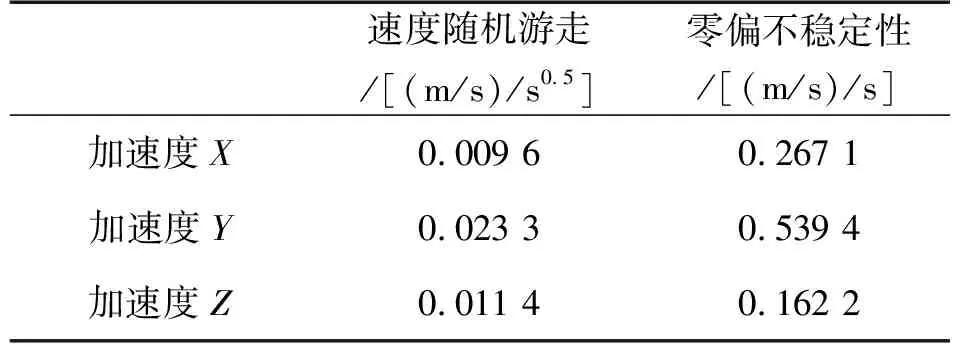
表1 加速度计主要误差系数(±10%估计误差)
参照文献[5]中Allan标准差与各项误差对应关系,结合图1可以看出:在T∈[0,101]时,曲线斜率为-1/2,速度随机游走为主要误差项,在T∈[101,102]时,曲线趋于水平,误差项为零偏不稳定性。即MEMS加速度计短时间内主要误差项为速度随机游走,长时间为零偏不稳定性误差。速度随机游走误差是由速率随机白噪声积分引起的具有随机游走特性的误差增量,是高频信号,可用白噪声表征[6]。而零偏不稳定性则用1/f噪声或者其他低频漂移表征。
1.2 MEMS加速度计噪声建模
由以上分析可知,加速度计输出信号中主要包含白噪声和1/f噪声。1/f噪声是一类具有长相关性、自相似性以及非平稳性的随机噪声,本文采用统计自相似信号较为经典的分数布朗运动(FBM)模型[12]:

(1)
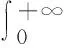
MEMS加速度计输出信号模型表示为:
f(t)=s(t)+n(t)+ω(t)
(2)
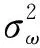
s(t)=ax=-βsin(2πft)
(3)
式中:β为常量,f为采样频率。
2 小波阈值去噪优化算法设计
基于上述构建的噪声模型,针对1/f噪声的长相关性和非稳定性,提出利用小波阈值去噪法将其滤除,下面设计一个基于多尺度阈值函数的MEMS加速度计去噪优化算法。
2.1 选取最优门限阈值
文献[12]表明,小波分解过程中1/f噪声在各尺度上可看作是均值为零的白噪声,因此,可以采用传统的平稳信号处理方法对小波系数进行滤波处理。传统的小波阈值去噪方法在各尺度上选用统一的阈值,但随着分解尺度的增加,噪声所引起的小波系数不断减小直至趋于稳定,这就要求阈值应随尺度增加而不断降低并趋于稳定,从而保留更多的有用信号。指数函数满足上述变化趋势,因此,本文在固定阈值的基础上进行改进,阈值表达式为:
(4)
式中:λj表示尺度j对应的阈值,N为信号长度,σ代表噪声水平,a、b、c为调节因子且b<0。调节因子的选取遵循以下规则:首先假定调节因子的取值范围,以一定间隔选取数值,根据式(4)计算各层阈值,以信噪比为定量分析指标,不断缩小取值范围最终可获取较为稳定可靠的经验值。
2.2 多尺度阈值函数设计
针对传统软、硬阈值函数存在的问题,近年来学者们陆续提出改进阈值函数[8-11],但它们都存在一定的缺陷:半软阈值函数计算复杂,实用性差;渐进半软阈值和遗传自适应阈值函数处理前后的小波系数仍然存在偏差;Xing阈值函数连续,且没有固定偏差,但在小于阈值部分小波系数滤除不完全,去噪不彻底。本文提出一种多尺度阈值函数,表达式如下:
(5)
式中:wj,k和j,k分别为去噪处理前后的小波变换系数,λ为阈值,m为调节系数,其定义域为m∈[0,1]。为了直观分析该阈值函数对小波系数的处理效果,绘制阈值函数输出曲线,如图2所示。

图2 多尺度阈值函数输出曲线
图2表明,当m=0时,大于阈值部分(由有用信号产生)保留原有小波系数,小于阈值部分(由噪声产生)则进行非线性滤除;m=1时,小于阈值部分全部去除,大于阈值部分当|wj,k|→+∞时小波系数无限逼近真实值wj,k(硬阈值处理后效果)。通过在各尺度上调节系数m可获得不同的滤除效果,m的选取满足以下原则:在不同尺度上,以硬阈值函数为基准,即小于阈值系数全部滤除,大于阈值部分保留原有系数,择优选取系数m,以达到最好的逼近效果。m的选取满足以下公式:
(6)
(7)
(8)

多尺度阈值函数优点在于:(a)函数在wj,k=λ处j,k(λ-)=j,k(λ+)=λ·(1-m),即函数在wj,k=λ处连续,解决了硬阈值函数在阈值处不连续的问题;(b)无论m取何值,|wj,k|≤λ时,j,k逼近0,去噪比较完全,|wj,k|>λ时,j,k逼近真实值wj,k,很大程度上减少了固定偏差;(c)多尺度阈值函数采用优化的思想,在各尺度上选择最优调节系数,有效地保留有用信号,滤除随机噪声。
3 实验验证及结果分析
3.1 仿真分析

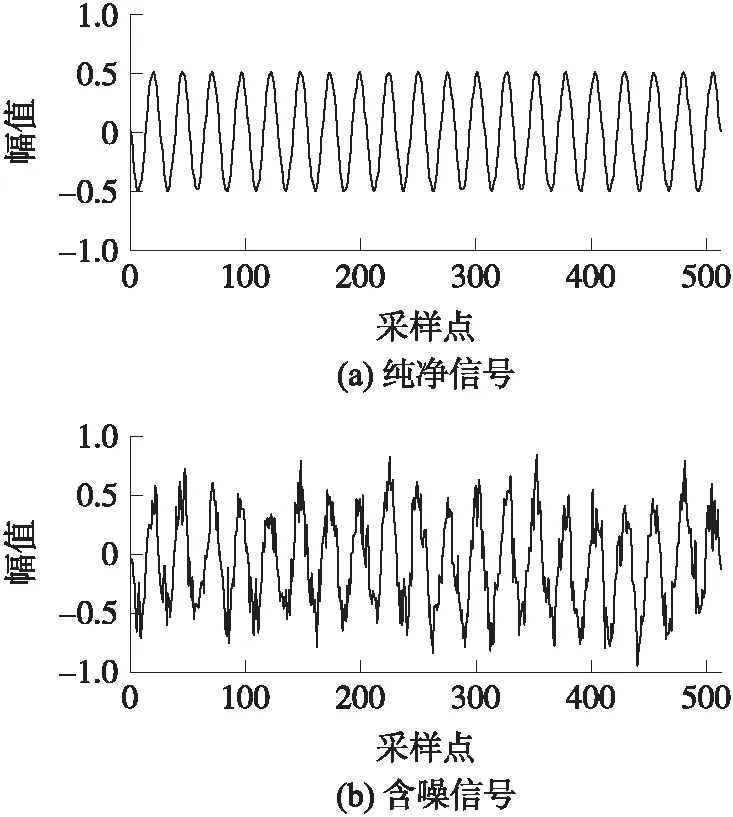
图3 纯净信号及含噪信号波形图
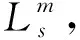

表2 各层选取不同调节系数的逼近程度
为了定量分析算法的有效性,选取信噪比(SNR)、均方根误差(RMSE)和波形相似度(S)作为指标来检验去噪的效果,不同阈值函数去噪评价指标比较如表3所示。

表3 不同阈值函数去噪评价指标比较
仿真结果表明,与传统阈值函数相比,改进阈值函数去噪效果更佳,其中,Xing阈值函数的去噪效果较为突出,而本文提出的多尺度阈值函数在其基础上提升了1.5 dB左右,均方根误差也有所降低。表3中Tc表示系统采用不同阈值函数去噪所用时间(英特尔赛扬CPU G540,内存:4 G),从中可以看出多尺度阈值函数去噪与其他方法相差不大。为了更加直观地分析去噪效果,选取传统阈值函数、Xing阈值函数和多尺度阈值函数去噪后信号进行对比分析,如图4所示。

图4 各阈值函数去噪效果对比图
图4(a)、(b)线框表明,硬阈值去噪后的信号出现局部振荡,而软阈值去噪后重构信号光滑,但硬阈值函数的更加接近原始信号。相较于传统的阈值函数去噪结果,Xing阈值函数和多尺度阈值函数去噪后重构信号都更加接近真实值,且曲线平滑,图4(c)、(d)线框表明,Xing阈值函数由于在小于阈值部分滤波不够完全,在重构信号中会出现少许的毛刺,而多尺度阈值函数在各尺度上选取不同系数逼近硬阈值函数,去噪较为完全,因此去噪效果更佳。
3.2 惯导系统实验分析
为了验证小波阈值优化去噪方法的实用性,对MPU-9250的静态和动态数据分别进行处理。首先,设置采样频率为50 Hz,将MPU-9250固定在水平面上,连续采集数据1 h,测得的加速计原始信号和小波去噪后信号(前10 s)如图5所示,数据结果如表4所示。

图5 静态加速度计信号小波去噪效果图
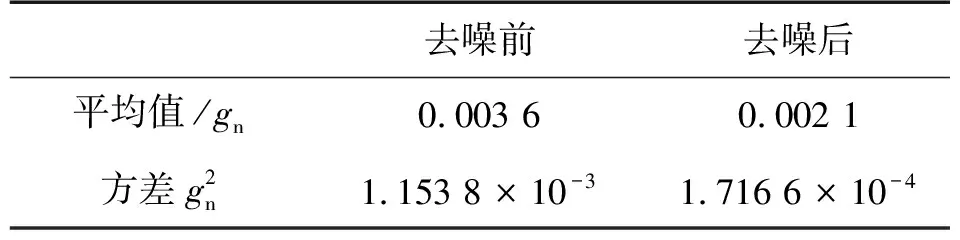
去噪前去噪后平均值/gn0.003 60.002 1方差g2n1.153 8×10-31.716 6×10-4
从图5可以看出,去噪后的信号明显更加稳定,表4表明,去噪后均值更加接近真实值,方差下降了一个数量级。
动态数据的测量采用以下方式:将运动传感器模块固定在高为1 m的手推车上,保持水平放置匀速直线行走30 m、50 m和100 m,不同长度各取5组数据。最后对测得的加速度双重积分直接求解位移,去噪前后的均方根误差如表5所示。

表5 去噪前后位移均方根误差
从表5可以看出,随着行走距离不断增大,加速度计的累计误差导致精度越来越低(加速度计漂移误差),而去噪之后位移的相对误差在20 m、50 m和100 m 的距离内分别降低了7.15%、4.26%和2.69%,由此可见,多尺度阈值去噪方法适用于惯导系统,且效果显著。
4 结论
为了有效地去除MEMS加速度计漂移误差,提高惯导系统的精度,本文提出了一种基于多尺度阈值函数的小波去噪优化算法,针对不同尺度,择优选取不同的调节系数从而提高去噪效果。仿真及实验结果证明,该方法可有效降低噪声方差,并在一定程度上提高系统导航精度。此外,本文提出的MEMS加速度计小波降噪方法也适用于陀螺仪和磁力计等其他惯性器件的去噪处理。
参考文献:
[1] Tian Z S,Zhang Y,Zhou M,et al. Pedestrian Dead Reckoning for MARG Navigation Using a Smartphone[J]. EURASIP Journal on Advances in Signal Processing,2014,2014(1):65.
[2] Li Z P,Fan Q J,Chang L M,et al. Improved Wavelet Threshold Denoising Method for MEMS Gyroscope[C]//11th IEEE International Conference on Control and Automation(ICCA),2014:530-534.
[3] 姜博文,王可东. 低成本车载组合导航在GPS失效时的算法设计[J]. 传感技术学报,2017,30(3):412-417.
[4] Wang H,Sen S,Elgohary A,et al. No Need to War-Drive:Unsupervised Indoor Localization[C]//10th International Conference on Mobile Systems,Applications,and Services ACM,2012:197-210.
[5] El-Sheimy N,Hou H Y,Niu X J. Analysis and Modeling of Inertial Sensors Using Allan Variance[J]. IEEE Transactions on Instrumentation and Measurement,2008,57(1):140-149.
[6] 孙淑光,王天游,程鹏,等. MEMS惯性传感器随机误差分析与去噪研究[J]. 计算机测量与控制,2016(3):291-295.
[7] 田晓春,陈家斌,韩勇强,等. 一种优化的小波阈值去噪方法在行人导航系统中的应用[J]. 中国惯性技术学报,2015(4):442-445.
[8] 魏文畅,杨俊杰,蔡建立. 基于小波变换的半软阈值参数算法研究[J]. 计算机工程与应用,2009(1):73-76.
[9] 周西峰,朱文文,郭前岗. 基于渐近半软阈值函数的超声信号去噪方法[J]. 探测与控制学报,2011(2):35-39.
[10] 邢国泉,叶华山,张玉霞,等. 基于一种新的阈值函数的小波图像去噪方法[J]. 生物医学工程学杂志,2013(4):743-747.
[11] Li J,Cheng C K,Jiang T Y,et al. Wavelet De-Noising of Partial Discharge Signals Based on Genetic Adaptive Threshold Estimation[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2012,19(2):543-549.
[12] 童姣叶,李荣宽,杜微. 基于小波分析的MEMS加速度计输出噪声消除[J]. 传感技术学报,2015,28(10):1503-1507.
[13] Lee H,Lee J,Cho J,et al. Estimation of Heading Angle Difference between User and Smartphone Utilizing Gravitational Acceleration Extraction[J]. IEEE Sensors Journal,2016,16(10):3746-3755.

