多元函数泰勒公式的张量表示

曹文飞， 韩国栋

(陕西师范大学 数学与信息科学学院，西安 710119)

我们正处在一个高新技术蓬勃发展的时代，数学对高新技术的发展发挥巨大的推动作用.正如应用数学家David[1]指出：很少有人认识到，被如此称颂的高新技术本质上是一种数学技术.因此，良好的数学教育在这个年代显得尤为迫切.高等数学教育是数学教育中不可缺少的重要环节，因而如何讲授好高等数学，给学生打好数学基础是一个重要的研究课题.

直观性、简洁性与统一性是高等数学教材设计中所遵从的一般原则[2].比如讲授一元函数的“积分”概念时，教材里通过极限给出积分的严格定义，但是此种定义比较抽象，一般都是通过积分的几何含义——面积来直观地理解积分的本质，从而让学生容易掌握积分的概念.另外，简洁性和统一性在数学教材设计也是应遵从的重要原则.比如在讲授多元函数积分定义时，一般教材里都借助二元函数来展示多元函数积分的定义，并用尽可能精炼的语言将此定义阐述清楚.相反，采用多元函数一般抽象形式并用冗长文字叙述的方式只会让初学者望而却步.由此可见，“简洁性”原则显得尤为重要.另外，多元与一元函数的积分定义在形式上可统一起来，这种统一性也有利于学生记住积分的定义.可是，在当前高等数学教材中，多元函数泰勒公式的表述显得艰涩难懂.具体来说，一方面相比于逐项展开形式的泰勒公式，通过多项展开式进行表达的泰勒公式虽有一定的简洁性，但仍显抽象复杂；另一方面，多元函数泰勒公式与一元函数泰勒公式在形式上不够统一.为此，本文借助张量与张量积[3]运算引入多元函数泰勒公式的一种新表达，这种表达具有直观理解性以及与一元函数泰勒公式在形式上统一性的优点，从而能够让学生轻松地掌握本知识点.

图1 张量的直观展示

2 张量简介

张量是矩阵[4-5]的高阶扩展，在信号处理、计算化学、计量心理学等领域有重要应用.通常的向量可视为一阶张量，矩阵可视为二阶张量.图1分别展示出行向量、矩阵与3阶张量的直观形式.4阶及以上阶张量可视为高维几何中的长方体.

图2 张量积示例

3 多元函数泰勒公式的张量表达

为了方便叙述，本文以三元函数的三阶泰勒展开式为例.设函数f(x,y,z)在点u0的邻域Nρ(u0)内是3阶连续可微的，设任意点u∈Nρ(u0)，点u0的坐标为(x0,y0,z0)，点u的坐标为(x,y,z)，坐标差分分别为Δx=x-x0，Δy=y-y0，Δz=z-z0以及Δu=(x-x0,y-y0,z-z0)T.

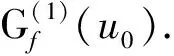
从上述例子可看出，一阶导数中每个元素针对x,y,z三个方向分别求偏导，通过这种扩展就得到二阶导数矩阵，二阶导数中每个元素针对x,y,z三个方向分别求偏导，通过这种扩展就得到三阶导数张量.更高阶导数可以依次类推得到.

基于上述函数导数的张量表示，给出三元函数泰勒展开式的一种新表达形式.回顾高等数学教材里的泰勒展开式[6]：

基于导数的张量表示以及张量积运算，不难验证：

将上述等式代入教材里提到的泰勒公式，我们得到多元函数泰勒展开式的一种新表达如下：

从上述新表达可看出：

(1)诸项的导数可通过几何拓展的方法得到，导数越高，通过几何拓展得到的张量阶数也越高，这种新导数表达具有直观的几何意义；

(2)右端展开式中的每项都由导数与坐标差分行向量的张量积组成，张量某模态与行向量的张量积就是张量切面与该行向量的线性组合之和，这种表示具有明确的几何含义；

(3)右端展开式可认为是一元泰勒公式的直接推广，因此新表达具有形式上的统一性.

综上所述，多元函数泰勒公式的新表达具有直观的几何含义和形式上的统一性，这些优点有利于学生们的理解和掌握，从而提高学生学习和应用泰勒公式的兴趣.

[参 考 文 献]

[1] 刘黄清.数学在现代科学技术体系中的地位和作用[J].杭州师范大学学报(自然科学版),2004,3(1):64-68.

[2] 王锦瑞.省属高校数学专业双语教学评价指标研究[J].西安文理学院学报(自然科学版),2016,19(6):7-11.

[3] KOLDA T G,BADER B W.Tensor decompositions and applications[J].SIAM Review,2009,51(3):455-500.

[4] 王新奇.矩阵的Kronecker积的应用[J].西安文理学院学报(自然科学版),2015,18(4):22-25.

[5] 宋占奎，莫德华，郭继.矩阵与线性空间直和研讨数例[J].西安文理学院学报(自然科学版),2009,19(1):100-102.

[6] 欧阳光中，朱学炎，金福临，等.数学分析[M].3版.北京：高等教育出版社，2007.