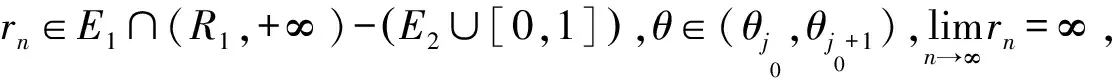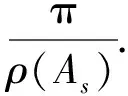一类高阶复微分方程解的增长性
覃智高,龙见仁,2*
(1.贵州师范大学数学科学学院,贵州 贵阳 550001;2.厦门大学数学科学学院,福建 厦门 361055)
1 引言和主要结果
本文中使用亚纯函数的 Nevanlinna 理论的标准记号,具体细节参看文献 [1-3].对复平面C上的亚纯函数f(z),用ρ(f),μ(f),ρ2(f) 分别表示亚纯函数f(z) 的级、下级、超级.为了行文的需要,还需要回顾如下定义.
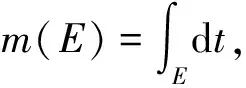
集合F⊂[1,+∞) 的上对数密度和下对数密度定义如下:
定义2设f(z) 为有穷正级整函数,S(α,β)={z:α 则称f(z) 在角域S(α,β) 内以指数形式趋于无穷.如果对任意θ∈(α,β) 有 则称f(z) 在角域S(α,β) 内以指数形式趋于零. 另外,还需要下面的定义. 本文中主要研究线性微分方程 f(k)+Ak-1(z)f(k-1)+…+A1(z)f′+ A0(z)f=0 (1) 解的增长性问题,其中Aj(z) 是整函数,j=0,1,…,k-1.从回顾两个典型的结果开始. 定理1[4]设Aj(z) 是整函数,j=0,1,…,k-1,若 max{ρ(Aj):j≠0}<ρ(A0),则方程 (1) 的任意非平凡解是无穷级. 定理3[6]设Aj(z) 是整函数,j=0,1,…,k-1,若 max{ρ(Aj):j≠0}<ρ(A0)<+∞,则方程 (1)的任意非平凡解f满足ρ2(f)=ρ(A0). 最近Long[11]研究了方程 f″+A(z)f′+B(z)f=0 (2) 解的增长性,其中A(z) 和B(z) 是整函数,得到下面的结果. 定理5[11]设A(z) 是方程 f″+P(z)f=0 (3) 的非平凡解,其中P(z)=anzn+an-1zn-1+…+a0,an≠0,n是非负整数,B(z) 是 Fabry 缺项级数,使得ρ(B)≠ρ(A),则方程 (2) 的任意非平凡解是无穷级. 本文研究了方程 (1) 解的增长性,获得了更为广泛的结果. 定理6设Aj(z) 是整函数,j=0,1,…,k-1,若存在s∈{1,2,…,k-1},使得As(z) 是方程 (3) 的非平凡解,A0(z)是Fabry缺项级数且ρ(A0)≠ρ(As),max{ρ(Aj):j≠0,s}<ρ(A0),其中P(z)=anzn+an-1zn-1+…+a0,an≠0,则方程 (1) 的任意超越解是无穷级. 注1定理 6的结论要求解为超越的,我们不知道超越解的条件是否可以去掉,其原因主要是在证明过程中使用了引理 4. 为了叙述下面的结果,需要使用杨-极值不等式函数及相关的定义.在亚纯函数的 Nevanlinna 理论中,亏值和 Borel 方向是非常重要的概念,Yang[3]获得了两者之间的关系,被称为杨-张不等式,Yang[12]利用定义 4 推广了杨-张不等式. 定义4[12]设f是C上满足 0<μ(f)<∞的亚纯函数,若对任意的ε>0 和任意的复数a∈C∪{∞},有 μ(f), 至多除去两个例外值,则从原点出发的半直线 argz=θ∈[0,2π) 叫做f的级≥μ(f) 的 Borel 方向,其中n(S(θ-ε,θ+ε,r),a,f) 是f-a在角域S(θ-ε,θ+ε,r)={z:θ-ε Wu[13]研究了杨-极值不等式函数,并获得了这类函数的很多性质,具体参看下面的引理 8. 下面的两个结果都涉及到杨-极值不等式函数. 定理8[11]设A(z) 是杨-极值不等式函数,B(z) 是 Fabry 缺项级数,则方程 (2) 的任意非平凡解是无穷级. 定理9[14]设Aj(z) 是整函数,j=0,1,…,k-1,若存在s∈{1,2,…,k-1},使得As(z) 是杨-极值不等式函数,A0(z) 满 足ρ(A0)≠ρ(As),max{ρ(Aj):j≠0,s}<ρ(A0),则方程 (1) 的任意非平凡解满足ρ2(f)≥ρ(A0). 下面的结果涉及具有有穷 Borel 例外值的整函数. 定理10[11]设A(z) 是具有有穷的 Borel 例外值的整函数,B(z) 是 Fabry 缺项级数,则方程 (2) 的任意非平凡解是无穷级. 结合前面几个结果,关于方程 (1) 解的增长性,得到了下面的结果. 定理11设Aj(z) 是整函数,j=0,1,…,k-1,若存在s∈{1,2,…,k-1},使得As(z) 是杨-极值不等式函数,A0(z) 是Fabry缺项级数,且max{ρ(Aj):j≠0,s}<ρ(A0),则方程 (1) 的任意非平凡解满足ρ2(f)≥ρ(A0). 注2相比定理9的条件,定理11包含了情形ρ(A0)=ρ(As),因此定理11获得了更为广泛的结果. 定理12设Aj(z) 是整函数,j=0,1,…,k-1,若存在s∈{1,2,…,k-1},使得As(z)为有穷的 Borel 例外值,A0(z) 是 Fabry 缺项级数,且max{ρ(Aj):j≠0,s}<ρ(A0),则方程 (1) 的任意非平凡解满足ρ2(f)≥ρ(A0). 引理1[15]设f是级为有穷的超越亚纯函数,对任意给定的常数ε>0,及满足k>j≥0 的 两个整数k,j,下列结论成立. (i) 存在对数测度有穷的集合E⊂(1,+∞),使得对任意满足 |z|∉E的z有 (ii) 存在线性测度有穷的集合F⊂(1,+∞),使得对所有满足 |z|∉F的z有 若f是一般的亚纯函数,则有如下的对数导数估计. 引理2[15]设f(z) 是超越亚纯函数,α(>1) 是常数,对任意给定的ε>0,存在对数测度有穷的集合E1⊂[1,+∞) 和常数B>0,B依赖于α和整数m,n,0≤m 引理3[16]设f(z) 为方程 (3) 的一个非平凡解,其中P(z)=anzn+an-1zn-1+…+a0,an≠0.令 j=0,1,…,n+1,θn+2=θ0+2π. 则f(z) 具有下列性质: (i) 在每个角域Sj内,f要么以指数形式趋于无穷,要么以指数形式趋于零; (ii) 若f在角域Sj内以指数形式趋于零,则f在角域Sj-1和角域Sj+1(若j=n+1 则Sj+1=S0) 内都以指数形式趋于无穷.然而,f可以在任意相邻的角域内以指数形式趋于无穷; (iv) 若在相邻角域Sj和Sj-1内f都以指数形式趋于无穷,那么对任意给定的ε>0,在角域 {z:θj-ε n(Ω(θj-ε,θj+ε,r),0,f)= 其中,n(Ω(θj-ε,θj+ε,r),0,f) 表示f在角域Ω(θj-ε,θj+ε,r)={θ-ε |As(z)|≥exp{(1+δ)α|z|β}, 对所有的j∈{0,1,…,s-1,s+1,…,k-1},有 |Aj(z)|≤exp{δα|z|β}. |f(j)(z)-bj|≤exp{-(1-kδ)α|z|β}; |f(m)(z)|≤exp{-(1-kδ)α|z|β}. logL(r,f)>(1-ε)logM(r,f), logM(r,g)>rρ(g)-ε, 引理6[11]设f(z) 是具有有穷的 Borel 例外值c的有穷级整函数,则f(z)=h(z)eQ(z)+c,其中h(z) 是整函数且ρ(h)<ρ(f),Q(z) 是多项式且 deg(Q)=ρ(f). 则存在一个正数R=R(ε)>1,使得当z∈Sj,j=0,2,…,2n-2,对所有满足 |z|=r>R的z有 Re{P(z)}>αn(1-ε)sin(nε)rn. 当z∈Sj,j=1,3,…,2n-1,对所有满足 |z|=r>R的z有 Re{P(z)}<-αn(1-ε)sin(nε)rn. 下面回顾杨-极值不等式函数的性质,设f是杨-极值不等式函数,argz=θk是f的级≥μ(f) 的q条 Borel 方向,k=1,2,…,q,0≤θ1<θ2<…<θq<θq+1=θ1+2π. 引理8[13]设A(z) 是杨-极值不等式函数,则 (i)μ(A)=ρ(A); C(θki,θki+1,ε,δ(ai,A))T(|z|,A), C(θki,θki+1,ε,δ(ai,A)) 是依赖于θki,θki+1,ε和δ(ai,A) 的正常数. 引理9[14]设A(z) 是杨-极值不等式函数,若存在 argz=θ∈(θj,θj+1),1≤j≤q,使得 定理6的证明根据定理的条件,如果ρ(As)<ρ(A0),则结论由定理1得证.故假设ρ(As)>ρ(A0),使用反证法,假设方程 (1) 存在一个有穷级超越解f.令 j=0,1,…,n+1,θn+2=θ0+2π. 应用引理3,分两种情况: 情形1.假设As(z) 在每个角域Sj都以指数形式趋于无穷,j=0,1,…,n+1.令b=max{ρ(Aj):j≠0,s}.由假设及文献[2] 知,对任意的θ∈(θj,θj+1),有 (4) |A0(z)|≤exp{|z|ρ(A0)+η}≤ (5) |Aj(z)|≤exp{|z|b+η}≤exp{|z|ρ(As)-2η}≤ (6) 因此在角域Sj中,j=0,1,…,n+1,当z→∞时,式(4)~(6) 成立.应用引理 4,在角域Sj(ε)={z:θj+ε 在Sj(3ε)={z:θj+3ε 利用 Phragmén-lindelöf 定理得 |f(s)(z)| 在整个复平面有界.由 Liouville′s 定理知,f在整个复平面是一个多项式,这与f是方程 (1) 的超越解矛盾.故结论得证. 情形2.若在n+2 个角域中至少存在一个角域,使得As(z) 以指数形式趋于零.不妨设As(z) 在Sj0={z:θj0 (7) |A0(z)|>exp{rρ(A0)-ε}. (8) 又因 max{ρ(Aj):j≠0,s}=b<ρ(A0) 知,存在R1>0,当r>R1时,有 |Aj(z)| (9) 应用引理 1,存在对数测度有穷的集合E2⊂(1,+∞),使得对所有满足 |z|=r∉(E2∪[0,1]) 的z有 (10) exp{rnρ(A0)-ε}<|A0(rneiθ)|≤ (1+o(1)). 当n充分大时,由ε的任意性知上式与b<ρ(A0) 矛盾.故方程 (1) 的任意超越解是无穷级. 应用引理 2,存在对数测度有穷的集合E4⊂(1,+∞),使得对所有满足 |z|=r∉E4∪[0,1] 的z有 假设ai是As(z) 的p个有穷亏值,i=1,2,…,p,argz=θj是As(z) 的 2p条ρ(As) 级 Borel 方向,j=1,2,…,2p,于是有 2p个角域Sj={z:θj C(θj,θj+1,ε,δ(ai,As))T(|z|,As), (11) 其中C(θj,θj+1,ε,δ(ai,As)) 是依赖于θj,θj+1,ε,和δ(ai,As) 的正常数,要么存在 argz=θ∈(θj,θj+1),使得 (12) (13) (14) (15) l=1,2,…,k-1. (16) 结合式(13)~(16)和(1)有 BT(2r,f)2k(1+|aj0|+ 由b+ε<ρ(A0)-ε及对充分大的n,有ρ2(f)≥ρ(A0). 定理12的证明设f是方程 (1) 的任一非平凡解,a是As(z)的一个有穷 Borel 例外值,由引理6有 As(z)=h(z)eQ(z)+a, j=0,1,…,2m-1, 应用引理7及ρ(h) |As(reiθ)-a|>exp{Crm}. (17) 对任意的z=reiθ∈Sj,j=1,3,…,2m-1,当r充分大时,有 |As(reiθ)-a| (18) 其中C是正常数.我们考虑m个角域Si中的一个,i=1,3,…,2m-1,不失一般性设为S1,于是对任意的z=reiθ∈S1,当r充分大时式(18) 成立.利用定理的条件及类似定理11的推导,存在点列zn=rneiθ∈S1,其中 limn→∞rn=∞,满足式(14)~(16)及(18).再次利用类似于定理11的证明方法得ρ2(f)≥ρ(A0). [1] HAYMAN W K.Meromorphic functions [M].Oxford:Qxford Mathematical Monographs Clarendon Press,1964:1-55. [2] LAINE I.Nevanlinna theory and complex differential equations[M].Berlin:Walter de Gruyter,1993:18-50. [3] YANG L.Value distribution theory [M].Berlin:Springer Verlag,1993:1-42. [4] FREI M. Über die lösungen linearer differential gleichungen mit ganzen funktionen als koeffizienten [J].Comment Math Helv,1961,35:201-222. [5] HELLERSTEIN S,MILES J,ROSSI J.On the gowth of solutions of certain linear differential equations [J].Ann Acad Sci Fenn Ser A I Math,1992,17:343-365. [6] CHEN Z X,YANG C C.Quantitative estimations on the zeros and growth of entire solutions of linear differential equations[J].Complex Var Elliptic Equ,2000,42:119-133. [7] LAINE I.Complex differential equations,in:handbook of differential equations,ordinary differential equations [M].Amsterdam:Elsevier,2008:1-35. [8] LONG J R,ZHU J,LI X M.Growth of solutions to some higher-order linear differential equations [J].Acta Math Sci Ser A Chin Ed,2013,33(3):401-408. [9] TU J,DONG T.Oscillation of complex high order linear differential equations with coefficients of finite iterated order [J].Elctron J Qual Theory Diff Equ,2009,66:1-13. [10] ZHANG C Y,TU J.Growh of solutions to linear differential equations with entire coefficients of slow growth [J].Electron J Diff Equ,2010,43:1-12. [11] LONG J R.Growth of solutions of second order complex linear differential equations with entire coefficients [J].Filomat,2018:32(1):275-284. [12] YANG L.Deficient values and angular disttibution of entire functions [J].Trans Amer Math Soc,1988,308(2):583-601. [13] WU S J.Some results on entire functions of finite lower order [J].Acta Math Sinica,1994,10(2):168-178. [14] LONG J R,QIU C H,WU P C.On the growth of solutions of a class of higher order linear differential equations with extremal coefficients [J].Abstr Appl Anal,2014,305710:1-7. [15] GUNDERSEN G G.Estimates for the logarithmic derivative of a meromorphic function,plus similar estimate [J].J London Math Soc,1988,37(2):88-104. [16] HILLE E.Lectures on ordinary differential equations [M].Ontario:California-London-Don Mills,1969:120-167. [17] LAINE I,YANG R H.Finite order solutions of complex linear differential equations [J].Electron J Diff Equ,2004,65:1-8. [18] MARKUSHEVICH A I.Theory of functions of a complex variable [M].Englewood Cliffs:Prentice Hall,1965:221-256.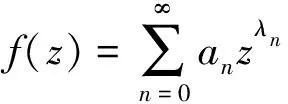
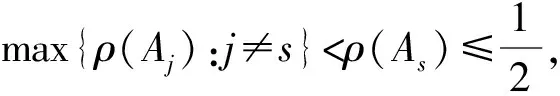


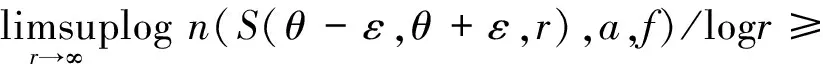
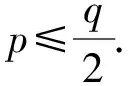

2 引 理

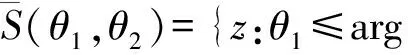





3 定理的证明