一种基于平行坐标系的车道线检测算法
王旭宸,卢欣辰,张恒胜,肖亚敏,解 梅
(电子科技大学信息与通信工程学院 成都 611731)
随着人工智能的大力发展,无人驾驶技术应运而生,在国家和各企业的大力投入下取得了一系列重大成果。从谷歌将“Waymo”[1](Alphabet旗下谷歌的无人驾驶汽车项目)宣布独立立项到百度将“阿波罗”计划[2](百度开放自动驾驶平台计划)成功开放,无人驾驶技术获得越来越多的关注和热议,相关领域也将对于无人驾驶技术的研究提上日程。
作为无人驾驶技术的基础工作,车道线检测技术的优劣关乎无人驾驶的成败。车道线检测的应用涵盖了无人驾驶的各个方面,包括自动泊车、变道检测、碰撞报警等。车道线检测是基于道路图像的特征点提取采样后,根据采样点的密集程度以及采样点之间的相关性进行线段提取,并由此确定车道线具体位置。由于道路图像的变化是实时的,所以对车道线检测的实时性会有较高的要求,不同算法的计算复杂度也因此得以体现。
针对车道线检测的道路数学模型有很多,如三次B样条[3-4]、双曲线[5-6]、抛物线[7-8]以及回旋曲线[9]等。然而在一般的行车过程中,通常以直线道路居多,所以直线检测算法便成为了车道线检测的重点研究方向。
基于OPENCV的车道线检测技术在PC机上无论准确率,还是检测速度都可以达到很好的效果。但若把算法移植到非x86的嵌入式硬件平台,将会造成检测速度剧烈下降,以致不能达到实时(20 帧/s以上)的要求。其原因主要是大多数车道线检测技术都采用OPENCV中的霍夫变换[10]来进行直线检测,而这种算法的实时性有待加强。
研究发现在平行坐标系中检测直线的准确率也很理想,且该算法可以大幅度降低算法的复杂度,加快算法的速度。基于此,将平行坐标系下检测直线的方法应用于车道线检测中。在实验中,以霍夫变换下的直线检测算法作为参照,对比平行坐标系下的直线检测算法,将二者的准确率和时效性做出对比分析。
1 预处理
车道线检测技术的关键性能指标是其准确率和时效性,而时效性的改进要在保证准确率的前提下进行。对道路图像进行预处理,将大幅缩减算法的搜索范围,降低图片信息量,对于提升算法的准确率和速度都将做出很大的贡献。而边缘检测作为线段检测的先期工作,进一步缩小了直线检测算法的搜索范围,其精确度也决定了检测效果的优劣。
1.1 图像分块
车载摄像头所采集到的道路图像如图1所示,常常会包含很多干扰信息,诸如天空、绿化带、护栏、建筑物等。

图1 车载摄像机采集的道路图像
通常采用图像分块的方法,将原始图片切割,以此确定感兴趣区域,以利于减少车道线搜索的范围,同时降低图像的信息量也利于提升处理速度。图2即为分块后的图像,略去了天空、路灯、部分绿化带等干扰因素。

图2 分块后的道路图像
1.2 图像二值化
我国的车道线有黄色和白色两种,针对白色车道线,将利用其灰度信息做后续处理,而黄色车道线在很多情况下并不能直接转化为灰度化的车道。

图3 二值化的道路图像
在这种情况下,对图像进行二值化处理[11],将图像像素点的灰度值设置为0或255,使整个图像呈现出明显的黑白效果。二值化图像会将图像的信息量减少,却能将图像边沿凸显出来。如图3所示,将黄色和白色车道不加区别的统一成二值化的车道信息,然后进行接下来的边缘检测。
1.3 边缘检测
边缘检测主要应用于检测图像的边沿部分,通常是不同的两部分区域交叉的边界。当图像的边界值出现跃变的时候予以标记,通常以离散点的形式来表示,并将道路的点标记图像作为直线检测算法的输入。在各种边缘检测算子中,canny算子[12-13]的检测效果较好,先使用双阈值判定边缘,用高阈值确定图像边缘,对于高阈值确定的、不能闭合的图像边缘,使用低阈值将其闭合,即在高阈值确定的边界邻域选取满足低阈值的点,如此反复,直至边界完全闭合。

图4 边缘检测的道路图像
边缘检测后的图像,保留了车道线的大部分信息且降低了图像所含的信息量,接下来将运用不同算法将车道线找出并加以标记。
2 霍夫直线检测算法
霍夫变换是一种常用的图像特征提取方法,通过投票机制检测具有某种特定形状的图像。这个过程在一个参数空间中通过累积计算结果的局部最大值,得到特定形状的参数,以此确定图形,并作为霍夫变换的输出。霍夫变换即运用两坐标空间之间的变换,将某个坐标空间上具有相同形状的曲线或者直线映射到另一坐标空间的某个点形成峰值,从而把形状检测问题转化为峰值的统计问题。
霍夫直线检测算法[14]是基于霍夫变换提出的一种图形提取算法。将笛卡尔坐标系下的直线中不同特征点标记在x-y坐标系中,如图5所示。依据直线方程式:

将直线上的各个点映射到k-b坐标下,原坐标系下的每个点对应新坐标系中的一条直线,此时的直线方程变为:

图5中各点映射到新坐标后,得到一簇直线,如图6所示。这簇直线的交点,即为原直线的参数k、b。
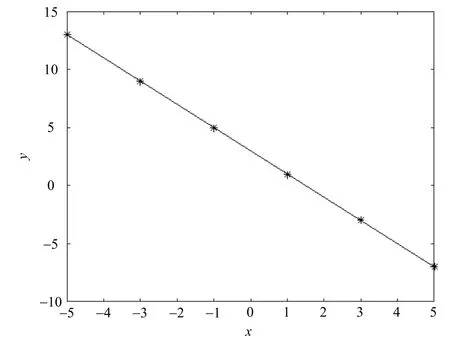
图5x-y直角坐标系下的直线
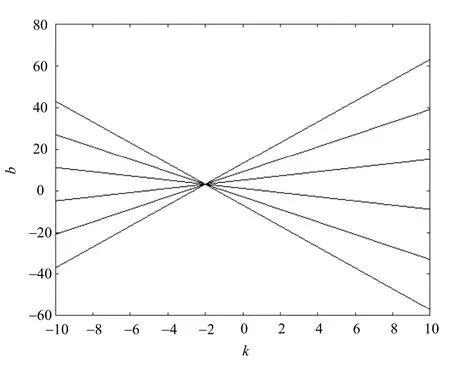
图6k-b直角坐标系下的直线映射
霍夫直线检测算法将直线检测转变为参数的估计,即参数点坐标的聚类问题,而对于直线形状的车道线,这种方法很实用。即便检测的对象变为弯道下的曲线形状,也可等效为若干直线的拼接后,再进行霍夫直线检测。
将边缘检测后的图像,通过霍夫变换把其中边缘标记点在x-y坐标系下的坐标映射到k-b坐标系下。此时散乱的直线簇出现了几个交点,如图7所示,这些交点所对应的坐标,即为在x-y直角坐标系下,检测到的对应位置的直线参数。
将图7所示的直线簇中各个交点坐标对应的直线标记在图像中,即可得到从图像中检测到的几条直线。由于图像中的离散点并不全都是车道线的边沿,为去除误检的线段,将检测到的一系列直线所经过的像素点值进行累加,按其像素点值进行排序,取前N个,像素值大于一定阈值的点保留,借此消除一定的噪声。经过筛选后,检测到的车道线如图8所示。
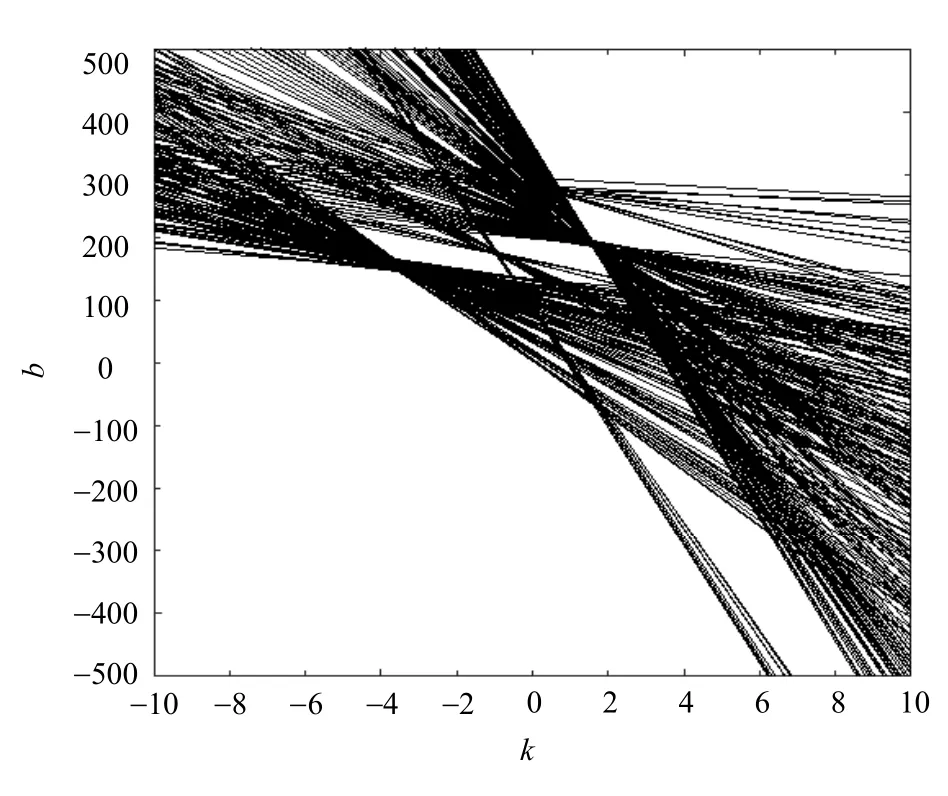
图7 道路边缘图像在k-b直角坐标系下的表示

图8 霍夫变换检测到的车道线
3 平行坐标系检测直线算法
平行坐标系是一种直观的坐标表示方法,可以将多元数据和高维几何图像可视化[15]。对n维空间上的点X(x1,x2,…,xn),用n条等距平行线作为坐标轴,分别将xi的值标记在第i根轴上对应地连接起来,形成一条折线,便将多维的数据表示在了平行坐标系中。如图9所示,为一个四维空间下的点集。
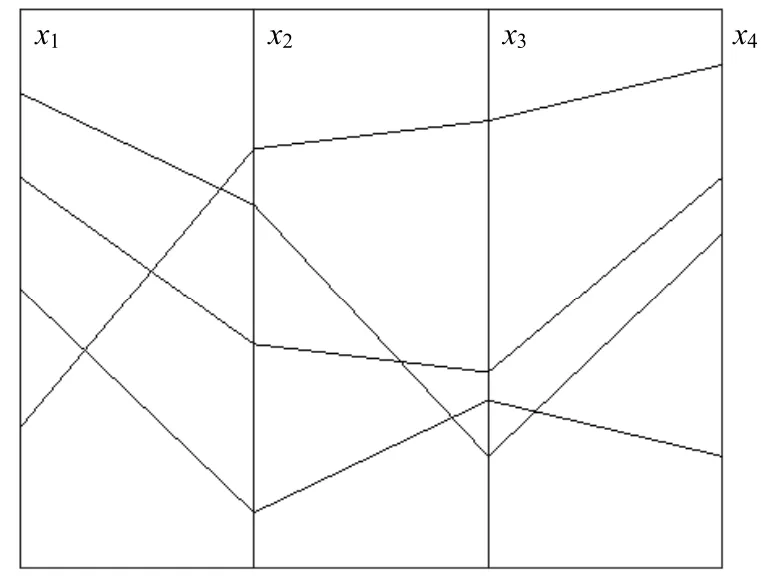
图9 四维空间点集在平行坐标系上的表示
对于道路这类二维图像,利用笛卡尔坐标与平行坐标的关系,将直线表示在平行坐标系下,即把直线上各点映射到平行坐标系中。
下面介绍平行坐标系检测直线的原理。设平行坐标系中-y轴与x轴之间的区域为T空间,x轴与y轴间的区域为S空间。首先在笛卡尔坐标系中设置一条直线:l ykxb=+(可表示除与y轴平行的任何直线),其上任一点可表示为(x,kx+b)。假设直线上3点分别为A(x1,kx1+b)、B(x2,kx2+b)和C(x3,kx3+b)。将平行坐标系表示在笛卡尔坐标系下,平行坐标系中的x轴位于笛卡尔坐标系下的y轴位置,平行坐标系中坐标轴间的宽度为d。
当斜率大于0时,A、B、C将在T空间中两两产生交点,得到的直线l1、l2、l3为:
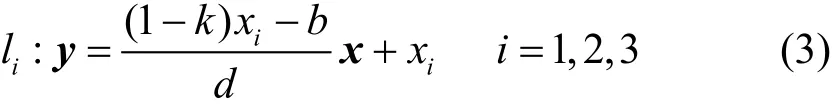
计算得到l1和l2的交点为:经验证,该点也在直线l3上,故3条直线交于一点。
同理,当斜率小于0时,A、B、C3点将在S空间中两两产生交点,得到的直线l1、l2、l3为:
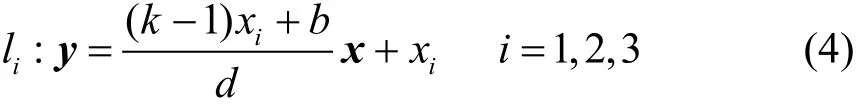
计算得到l1和l2的交点为:经验证,该点也在直线l3上,故3条直线交于一点。
由此可知,在直角坐标系中的一条直线对应平行坐标系中的一个点,而斜率正负不同的直线在平行坐标系中处于不同空间。斜率大于0的直线交点在T空间中;斜率小于0的直线,交点在S空间中。这为平行坐标系检测直线提供了理论基础。以斜率小于0为例,某条直线的平行坐标表示,如图10所示。
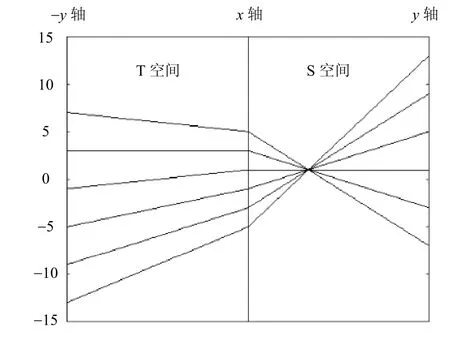
图10 二维空间直线在平行坐标系下的表示
设一条直线方程为y=kx+b,在平行坐标系中的表示点为(u,v),代入上述式(3)、式(4)得出在T空间中的对应关系为:

在S空间中的对应关系为:


式中,d表示坐标轴之间的距离。
将利用平行坐标系检测直线的原理应用到车道线检测之中,把边缘检测得到的图像中各个边缘点表示在平行坐标系中,如图11所示。其中折线的交点即代表检测到的某条直线的参数坐标。
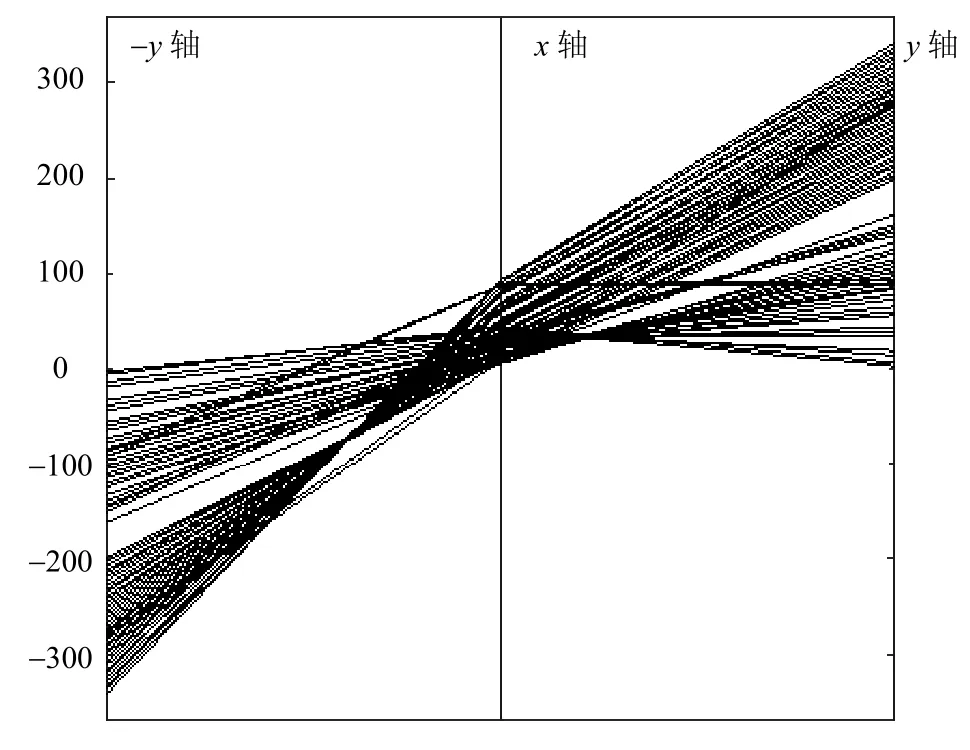
图11 道路边缘图像在平行坐标系下的表示
因为车道线大部分为一侧为正斜率,一侧为负斜率,故在平行坐标系T区域和S区域分别检测两侧车道线。在S区域和T区域分别对连线经过的像素点值进行累加,取前N个像素点值最大的点,对这些点进行去干扰处理。将去干扰后得到点的像素值取均值,若均值大于或等于像素阈值,则对去干扰后得到点的坐标值取平均,该坐标值的点即为对应检测区域中检测到的直车道线;如平均值小于像素阈值,则认为所在区域没有检测出车道线。车道线检测效果,如图12所示。

图12 基于平行坐标系的直线检测方法得到的车道线
4 结果分析与性能对比
车道线检测的首要目标是要正确检测出车道线,在准确率足够高的情况下保证实时性,能够尽快的识别跟踪道路图像。通过对两种算法的分析,可以确定两种直线检测算法对于车道线检测都是可行的。在仿真实验中,将再对它们的准确率和实时性进行对比分析。
4.1 准确率验证
车道线检测的目的是为了辅助驾驶,在进行检测的过程中,采用人眼进行识别,大致不偏离正确车道即可,但这种方法受主观因素影响很大。
本文采用人工标定的方法判别是否准确。首先标注两侧车道线的基准线l',每一根车道线标定两点,尽可能处于车道线的中心且两点间距离尽可能远,以确定车道线的位置,l'与图像底部交点x'。标定车道宽度w,在道路图像中选取较大的w。在标定过程中,检测直线和图像底部交点x与基准线和图像底部交点x',满足|x-x′|≤w,且检测直线与基准线满足|θ(l-l′)|≤10°,则认为检测到的车道线是正确的。在不同场景下,计算两种算法的准确率,如表1所示。两种算法在不同场景下的准确率差别不明显。
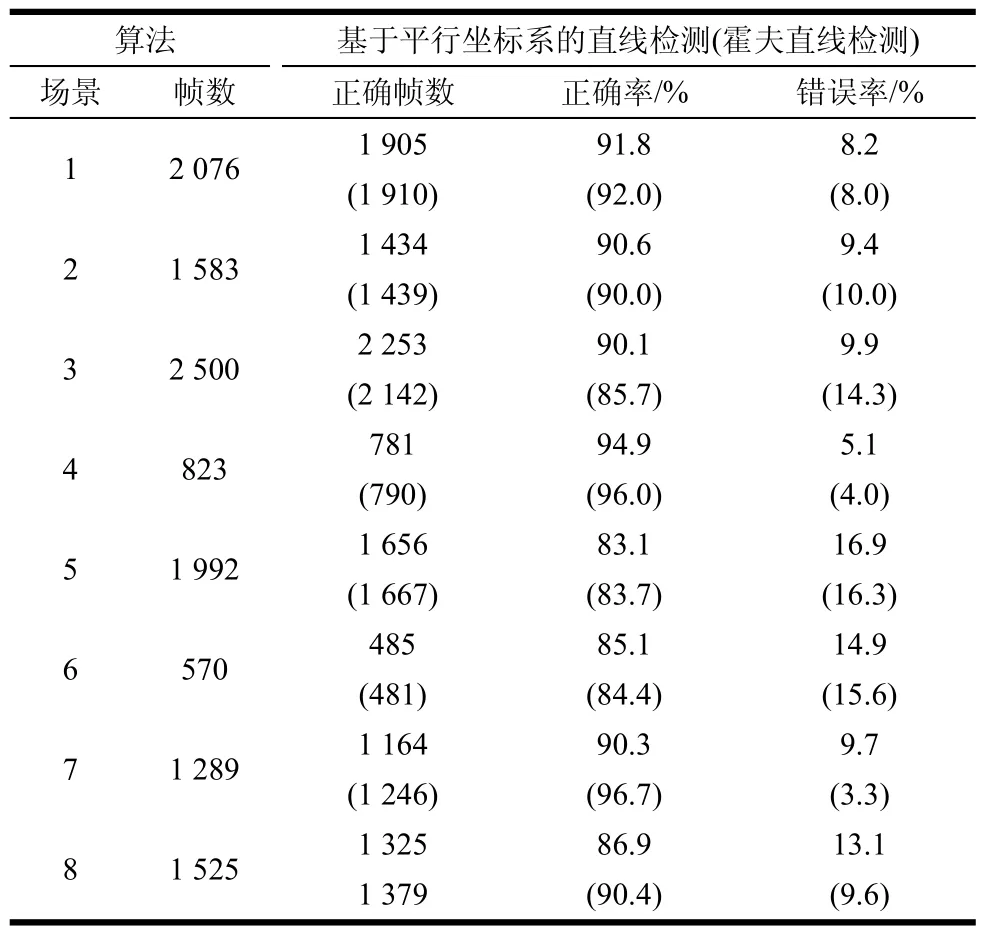
表1 准确率对比
4.2 时效性验证
表2所示为两种算法的实时性,以帧率(f/s)为单位进行对比。虽然二者都能满足实时性需求(帧率≥20),但是基于平行坐标系检测直线算法的检测速率显著高于霍夫直线检测算法。
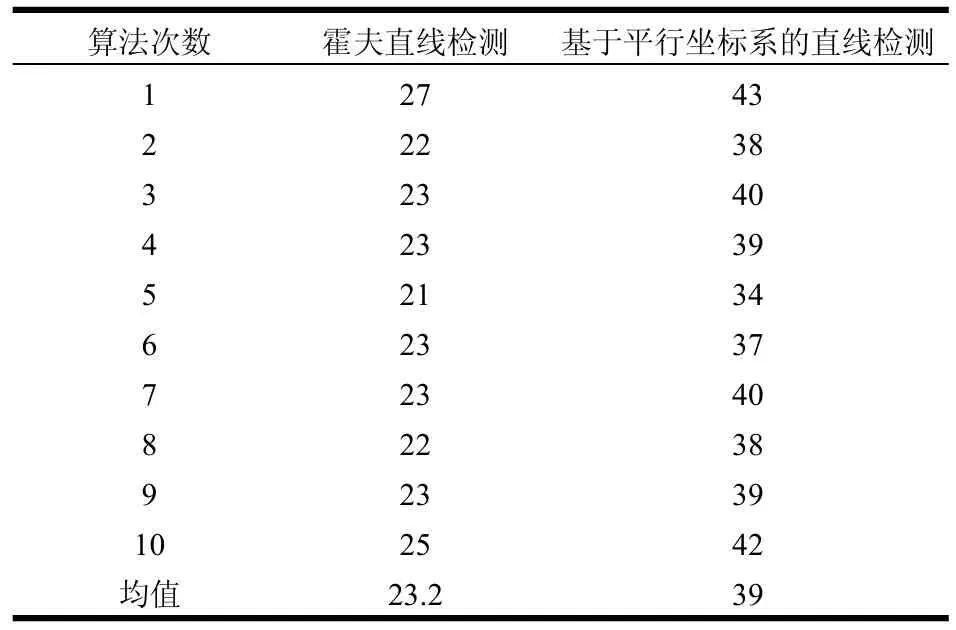
表2 算法速度对比
在本文中,两种算法除了在进行车道线检测部分采用不同直线检测方法外,其他步骤均相同。但是基于平行坐标系的车道线检测算法明显加快,究其原因是该算法在进行坐标映射时,不需要重新进行计算,而基于霍夫变换的车道线检测算法,需要逐点计算,影响了算法的效率。
5 结束语
本文将基于平行坐标系的直线检测方法应用于车道线检测,并将基于霍夫变换的直线检测方法和基于平行坐标系的直线检测方法进行对比。通过仿真验证两种检测方法的准确性和时效性,实验证明,基于平行坐标系的直线检测方法具有更高效的特性,能很好地满足车道线检测的实时性需求。
现有的车道线检测方法较庞杂,很少有能适用于多种路况下的检测算法。近年来,随着深度学习算法的快速发展,为智能交通带来了新的希望,未来的车道线检测技术将得到更快的发展,以达到无人驾驶的需求。
[1]ETHERINGTON D, KOLODNY L. Google’s self-driving car unit becomes Waymo[EB/OL]. [2016-12-13]. https://techcrunch.com/2016/12/13/googles-self-driving-car-unitspins-out-as-waymo.
[2]李根.百度宣布开放自动驾驶平台,取名“阿波罗计划”[EB/OL]. [2017-04-19]. http://tech.sina.com.cn/it/2017-04-19/doc-ifyeimqc4772869.shtml.LI Gen. The forthcoming of ‘Appollo’, an autopilot platform,has announced by Baidu. [EB/OL]. [2017-04-19]. http://tech.sina.com.cn/it/2017-04-19/doc-ifyeimqc4772869.shtml.
[3]WANG Y, TEOH E K, SHEN D. Lane detection and tracking using B-Snake[J]. Image & Vision Computing,2004, 22(4): 269-280.
[4]LI S, XU J, WEI W, et al. Curve lane detection based on the binary particle swarm optimization[C]//Control and Decision Conference. Melboume: IEEE, 2017.
[5]CHEN Q, WANG H. A real-time lane detection algorithm based on a hyperbola-pair model[C]//Intelligent Vehicles Symposium. Tokyo: IEEE, 2006: 510-515.
[6]LI X, FANG X, WANG C, et al. Lane detection and tracking using a parallel-snake approach[J]. Journal of Intelligent &Robotic Systems, 2015, 77(3-4): 597-609.
[7]MCCALL J C, TRIVEDI M M. Video-based lane estimation and tracking for driver assistance: survey, system, and evaluation[J]. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(1): 20-37.
[8]WANG X, WANG Z, ZHAO L. Lane detection and fitting using the artificial fish swarm algorithm (AFSA) based on a parabolic model[C]//The 9th International Conference on Applied Energy. Cardiff: [s.n.], 2017: 381-388.
[9]EIDEHALL A, GUSTAFSSON F. Obtaining reference road geometry parameters from recorded sensor data[C]//Intelligent Vehicles Symposium. Tokyo: IEEE, 2006: 256-260.
[10]DUDA R, HART P. Using the Hough transforms to detect lines and curves in pictures[C]//Commun ACM. California,USA: ACM, 1972: 11-15.
[11]王强, 马利庄. 图像二值化时图像特征的保留[J]. 计算机辅助设计与图形学学报, 2000, 12(10): 746-750.WANG Qiang, MA Li-zhuang. Reservation of features of binary images[J]. J Comput-Aid Desig Comput Graph,2000, 12(10): 746-750.
[12]陈强, 朱立新, 夏德深. 结合Canny算子的图像二值化[J]. 计算机辅助设计与图形学学报, 2005, 17(6):1302-1306.CHEN Qiang, ZHU Li-xin, XIA De-shen. Using the canny operator in the binary processing of images[J]. J Comput-Aid Desig Comput Graph, 2005, 17(6): 1302-1306.
[13]ZHAO M, LIU H, WAN Y. An improved Canny edge detection algorithm based on DCT[C]//IEEE International Conference on Progress in Informatics and Computing.Shanghai: IEEE, 2016: 234-237.
[14]KANG W J, DING X M, CUI J W, et al. Fast straight-line extraction algorithm based on improved Hough transform[J]. Opto-Electronic Engineering, 2007, 34(3):105-108.
[15]王绍敏, 孙晓静, 王克峰, 等. 应用平行坐标系进行可视化优化设计[J]. 计算机与应用化学, 2004, 21(1):11-15.WANG Shao-min, SUN Xiao-jing, WANG Ke-feng, et al.Visual optimization design using parallel coordinate system[J]. Computer and Applied Chemistry, 2004, 21(1):11-15.

