趋优算子和Levy Flight混合的粒子群优化算法

张新明，王 霞，涂 强，康 强

(1. 河南师范大学计算机与信息工程学院 河南 新乡 453007；2. 河南省高校计算智能与数据挖掘工程技术研究中心 河南 新乡 453007)

使用传统的优化方法已经无法有效地解决现实中的许多优化问题，因此，近年来引进了大量的自然启发式算法。自然启发式算法又称为智能优化算法，受启发于自然界生物的社会行为等。粒子群优化(particle swarm optimization, PSO)算法[1]作为较早的自然启发式算法，它模拟了鸟群或鱼群捕食时的社会行为。该算法因需调整的参数较少和易于实施的优势在许多优化问题上被广泛使用，但仍然存在早熟收敛、极易陷入局部最优等问题。针对PSO存在的问题，研究人员已经提出了许多基于PSO的改进算法[2-10]，目的在于提高PSO的优化性能。文献[2]通过反向学习与局部学习的协同行为，提出了具有反向学习和局部学习能力的PSO算法(reverselearning and local-learning PSO, RLPSO)。文献[3]结合自适应劳动分工模块，采用凸算子和反射算子，提出了自适应劳动分工的PSO算法。文献[4]将PSO与两种人类最好的学习策略(包括自我调节惯性权重、在全局搜索方向进行自我认知)进行结合实现算法的快速收敛，提出了一种自我调节PSO算法(self regulating PSO, SRPSO)。文献[5]针对PSO的早熟收敛问题，引进5次连续变异策略，提出了一种增强领导者的PSO算法(enhanced leader PSO, ELPSO)。文献[6]结合PSO和Levy Flight算子，提出了嵌入Levy Flight的PSO算法(PSO with Levy Flight, LFPSO)。文献[7]结合动态概率PSO算法的特点，提出了一种基于异构多种群策略的DPPSO算法。文献[10]提出了一种自适应惯性权重策略，每一个粒子在不同维都有它自己的惯性权重，是一种新的基于自适应惯性权重的PSO算法。但以上算法或多或少存在如下问题：优化效率不高，普适性不强等。另外，在现有的改进算法中，许多是对PSO的基本参数进行研究和改进，以便提高算法的性能。在PSO参数研究文献中，对惯性权重ω、学习因子1c和2c参数研究较多，但对速度边界参数Vmax和Vmin研究甚少。

本文针对LFPSO存在的问题，首先改进Levy Flight，然后引进趋优算子，并使趋优算子与改进的Levy Flight算子交替执行；最后对固定速度边界采用动态调整策略，构成改进的LFPSO(improved LFPSO,ILFPSO)算法。

1 LFPSO算法

图1 LFPSO算法流程图

LFPSO算法[6]将Levy Flight嵌入到PSO算法中，用于解决PSO的早熟收敛和全局搜索能力不足的问题。Levy Flight是一种非高斯随机过程，是从Levy稳定分布中提取的随机游走方式，确保了PSO可以更有效地进行全局搜索而不会陷入局部停滞。LFPSO算法为每个粒子的试验次数设置一个阈值，在阈值以内的粒子速度与其位置更新如下：

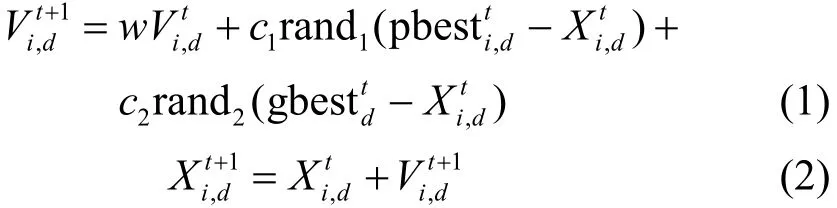
而超出阈值时，粒子则执行Levy Flight操作，对粒子的位置进行重新分配：

式中，符号⊕表示数组中每个对应元素的乘法运算。LFPSO算法的基本流程图如图1所示。其中，trial(i)表示第i个粒子当前的试验次数，limit表示为每个粒子设置的阈值。值得注意的是：若更新后的粒子较优，trial(i)重置为0，否则trial(i)就加1。

2 趋优算子与Levy Flight混合的粒子群优化算法(ILFPSO)

2.1 LFPSO存在的问题

LFPSO存在的两大问题：1) 由于Levy步长的计算公式中参数β的取值范围为(0,2)，不合适，有可能产生无效解。2) 由于LFPSO是针对原始的PSO全局搜索能力差的问题引进Levy Flight，用于提高全局搜索能力；虽然全局能力有所提升，但仍然存在收敛速度慢，优化效率低和普适性不强的问题，其主要原因是探索与开采没有达到平衡。现代智能优化算法不是仅追求全局搜索能力或者局部搜索能力单方面的提升，而是考虑二者的平衡，这样才能提高算法的整体优化性能。针对以上问题，ILFPSO有3点创新：

1) 改进Levy Flight以减少无效解；

2) 将既有一定的全局搜索能力又有较强的局部搜索能力的趋优算子与改进的Levy Flight融合，使其全局搜索能力和局部搜索能力同时提高，二者达到平衡；

3) 将LFPSO中固定的速度边界改为动态调整，以便搜索前期易于找到全局最优点，后期容易获得局部最优解，也用于平衡探索与开采能力。

2.2 改进的Levy Flight算子

Levy Flight作为一种随机游走方式，其长跳跃的搜索方式与偶尔短跳跃的搜索方式交叉执行，保证了算法能够及时跳出局部最优点，扩大了粒子的搜索范围。Levy分布中，参数β影响较大，其小值执行长距离跳跃，防止陷入局部最小值。由于Levy步长中β的取值范围是(0,2]，不够合适，在低值区域易产生无效的σ，最终产生无效的粒子。本文将Levy分布中参数β的取值范围更精确选择为[0.1,2]，防止产生无效解。参数β取值的程序伪代码见算法1。

算法1：β取值限定

求解Levy分布中的β值：β=2∗rnd；

根据式(4)求解步长s

其中，rand表示在区间[0,1]中均匀分布的随机数。Levy分布中的步长s为：

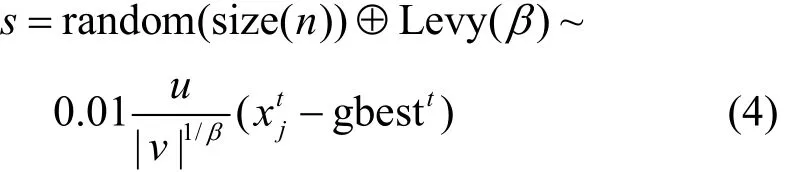
式中，u和v分别服从正态分布[6]：

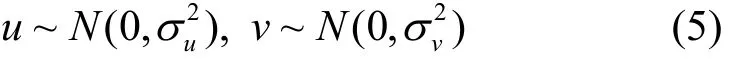
式中，

式中，Γ是标准的伽马函数。从式(4)中获得步长s值来更新第i个粒子iX的位置。

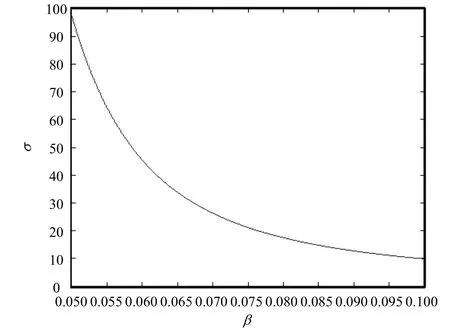
图2 参数β与σ值的关系曲线

通过分析可知，参数β影响着σ的取值。通过大量的实验发现：

1)β取值为区间[0,0.000 3]之间的随机数时，σ为无穷值(即无效)，导致s为无效值。

2)β取值为区间[0.000 3,0.1]之间的随机数时，σ过大，它又导致两种结果：①s过大，随机步长过大，此跳跃无意义；②s趋于0，使此跳跃在实质上未发生。为了能更清晰地看出参数β对σ值的影响，参数β取[0.05,0.1]之间的数，β对σ值的影响曲线如图2所示。从图2可知，随着参数β减少，σ值呈指数级增加，进而无效。

2.3 趋优算子

文献[11]提出了一种全局最优和声搜索算法，该算法首次使用了趋优算子，见算法2，通过将最优和声的信息赋给当前和声，提高了搜索能力。从算法2可知，趋优算子充分地利用了群体历史最优解的位置信息，从解的角度向群体中当前最优解趋近，故称趋优算子[11-12]；从维的角度发生突变，通过随机选取最优解中某一维度的值直接替换当前维度的值，提高全局搜索能力。此算子主要体现在局部搜索能力上，全局搜索能力有限，所以从总体上讲，更侧重于提高算法优化精度和收敛速度。

2.4 Levy Flight算子与趋优算子有机融合

使用趋优概率pa将Levy算子与趋优算子交替运行。当均匀分布在[0,1]中的随机数小于0.5时，趋优概率pa取值为0.5，否则取值为0.99。采取这样的随机选取方式，减少了人工选取pa参数的过程。下面分别对两种趋优概率的情况进行分析：

1) 当pa=0.5时，趋优算子与Levy算子交替运行的概率均等。若随机数大于pa值，执行趋优算子，获取一个随机维，将全局最优解随机维的值赋给当前维。此时，当前粒子向当前最优位置趋近，加快了收敛速度。若小于pa值，执行Levy算子，提高全局搜索能力。两种算子的交叉执行，提高了算法的整体搜索能力。

2) 当pa=0.99时，趋优算子运行的概率极小，多数情况下仅执行改进的Levy Flight操作，更强化全局搜索，且改进的Levy Flight算子防止产生无效解。

2.5 速度边界的动态更新

本文将LFPSO算法中的恒定速度边界值改为对速度的边界动态更新。首先设置动态边界的极值(最大值0v和最小值1v)，然后动态调整，随着迭代次数的增加，速度的上边界maxV由大变小。在每次迭代中，对粒子的速度边界更新公式为：

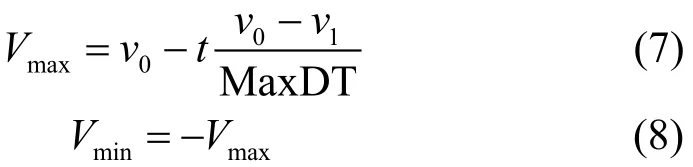
式中，minV为速度的下边界；t为当前迭代次数；MaxDT为最大迭代次数。原算法中，固定的速度边界值不利于探索与开采的平衡。而在ILFPSO中，由于引进了动态更新机制，前期阶段，算法中的粒子分布范围较为广泛，根据式(2)，若粒子速度大，其位置变化范围大，即扩大了粒子的搜索空间，增加了找到全局最优值的概率；而在后期阶段，粒子分布相较于前期较为集中，粒子速度小，其位置变化范围小，即缩减了搜索空间的范围，增加了粒子寻找局部最优值的概率，提高了搜索精度，从而提高了局部搜索能力。因此，动态的速度边界调整机制有利于寻找全局和局部最优解，即前期有利于搜索全局最优解，后期能加快算法的收敛速度。

2.6 ILFPSO算法流程

基于以上3点创新，ILFPSO的算法流程如下：

1) 初始化参数。参数包括学习因子1c和2c、试验次数trail、阈值limit等。2) 随机初始化种群的位置和速度，计算适应度值，选择个体历史最优值pbest和全局最优值gbest。3) 用式(7)和式(8)动态更新速度边界，随机选取趋优概率pa的值。4) 若trail(i)未超过limit，则对粒子的速度和位置按式(2)更新，并进行边界检查。否则执行流程5)，并将trail(i)重置为0。5) 当随机数大于pa，则执行趋优算子，否则执行改进的Levy Flight算子。6) 计算粒子的适应度值，更新trail(i)，并更新个体历史最优解pbest和全局最优解gbest。7) 判断是否满足终止准则，若满足则算法终止，否则返回流程3)。

ILFPSO融入了3点创新，提升了优化效率，较好地平衡了探索与开采能力，提高了算法整体性能。

3 仿真实验及结果分析

3.1 测试函数与实验环境

为测试本文提出的ILFPSO算法的寻优能力，选用4类benchmark函数进行仿真实验，分别为：单峰函数、多峰函数、平移函数和旋转函数[13]。表1和表2给出了这4类28个benchmark函数的名称、搜索范围和理论最优值(Fmin)情况，函数的相关表达式见文献[3-6,13]。单峰函数只有一个全局最优点，适合用于评估算法的开采能力；多峰函数有多个局部最优点，适合用于评估算法的探索能力；平移函数和旋转函数用于评估优化算法解决复杂优化问题的能力。

选取这28个benchmark函数，目的在于检测ILFPSO算法的优化性能，通过与国外学者提出的LFPSO算法、增强领导者粒子群算法(ELPSO)、自我调节粒子群优化算法(SRPSO)进行优化性能、收敛性、运行时间的对比，验证ILFPSO的优越性。所有的仿真实验均在操作系统为Windows 7、CPU为主频为3.10 GHz和内存为4 GB的PC上进行，编程语言采用MATLAB R2014a。

表1 单峰和多峰benchmark函数信息表

表2 平移和旋转benchmark函数信息表

3.2 优化性能对比

为了控制参数对各个算法性能的影响，也为了公平起见，所有算法的最大迭代次数都设为2 500，种群数量都设为20，函数的维数n设为30。ILFPSO最大速度初值0v和终值1v分别设置为位置边界最大长度的20%和0.1%，学习因子1c、2c和惯性权重因子w同LFPSO参数设置。LFPSO、ELPSO和SRPSO参数设置见相应的参考文献。表3和表4分别给出了4种算法在28个benchmark函数上30次独立运行的寻优结果减去理想最优值(Fmin)后(除f15以外)的最大值(Max)、最小值(Min)、均值(Mean)和方差(Std)，其中黑体代表算法中的最优者。

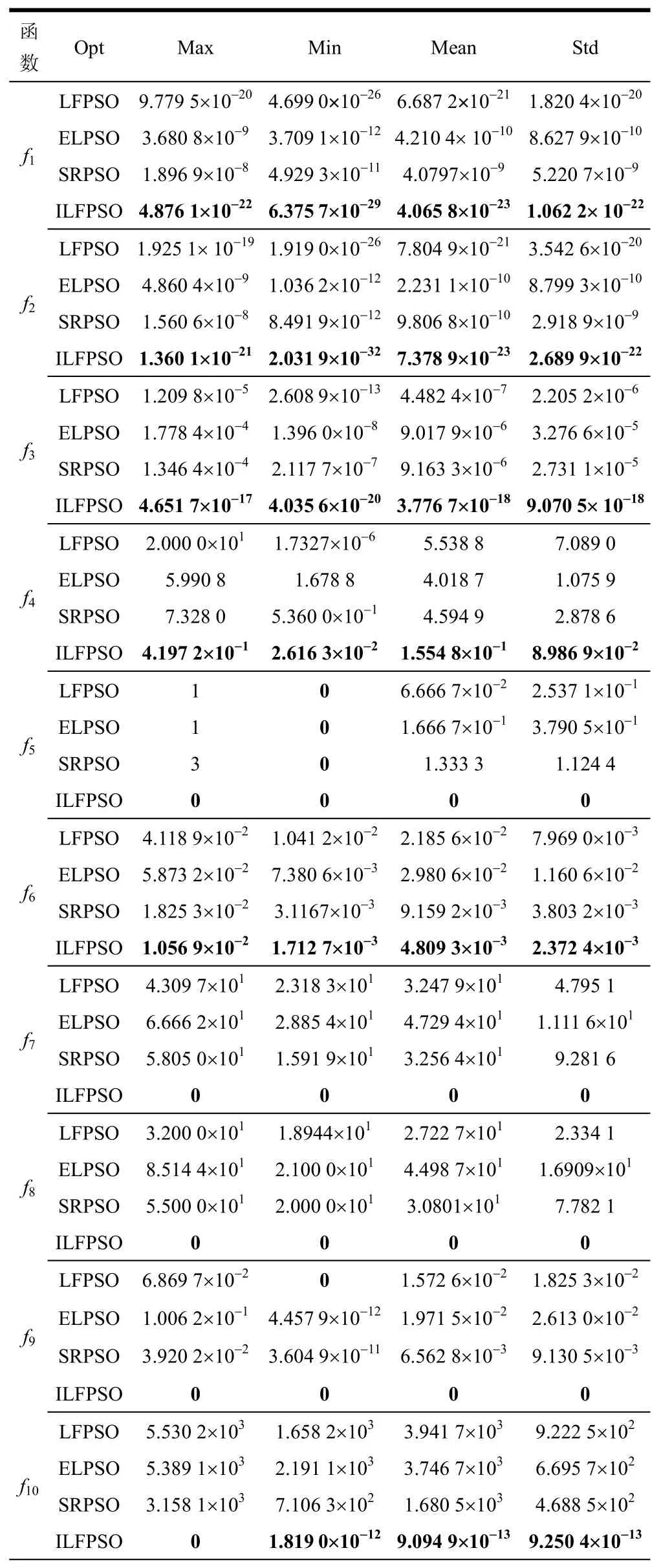
表3 4种函数对单峰和多峰函数的性能测试结果

续表

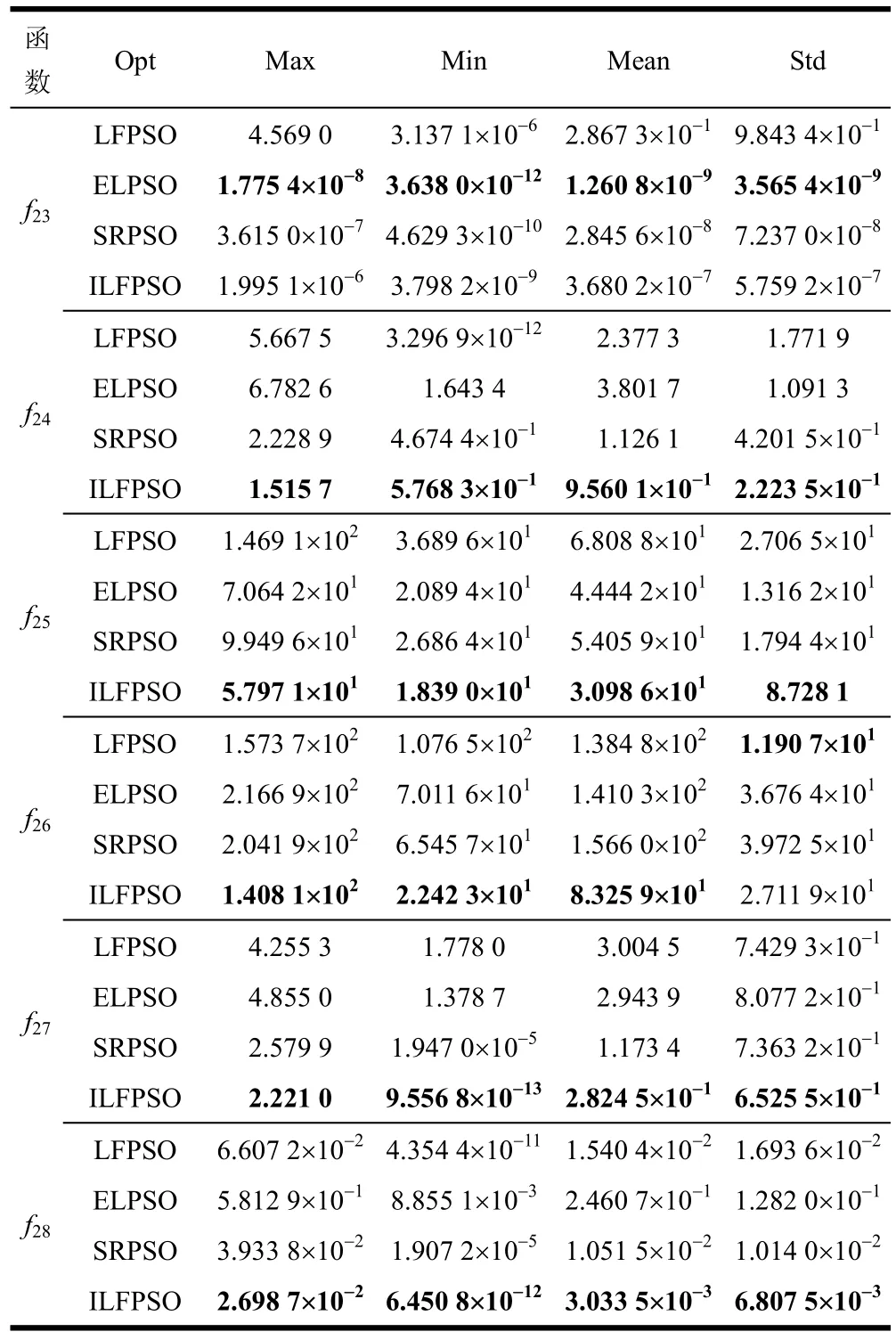
表4 4种算法对平移和旋转函数的性能测试结果

采用单峰函数进行算法的性能测试，主要是检测算法的局部搜索能力和收敛精度。4种算法在7个单峰函数f1～f6和f19上的性能测试数据看出，在Max、Min、Mean和Std上，与LFPSO、ELPSO、SRPSO相比，ILFPSO均表现了优异的开采能力。这说明具有较强局部搜索能力的趋优算子融合到Levy Flight中和动态调整速度边界这两项改进是有效的，提高了算法的局部搜索能力和收敛精度，尤其在f3、f4和f19上大幅度领先于LFPSO。

通过使用15个多峰函数f7～f18，f20～f22对4种算法进行性能测试，以检验算法的全局搜索能力。对于多峰函数f7～f15、f17、f18、f20、f22，ILFPSO明显优于其他3种对比算法，效果最好。在Max、Min和Mean上，ILFPSO均获得了最小值，说明该算法在求解多峰函数时全局搜索能力较强。在Std上，ILFPSO也都获得了最小的值，这说明其稳定性最强。当求解函数f16、f21时，ILFPSO的性能测试结果相对来说稍差，但对于求解函数f16时，在Mean上，ILFPSO获得了最好的结果；在Std上，则是SRPSO表现了最优的性能，ILFPSO次之；在Max上，SRPSO获得了最好的值，ILFPSO次之；在Min上，ELPSO获得了最小的值，ILFPSO次之。而对于函数f21，ELPSO表现的寻优能力最优，ILFPSO次之。但是相对于LFPSO，ILFPSO具有更强的搜索能力，这说明趋优算子与Levy Flight算子融合是有效的，能很好地平衡全局和局部搜索能力，使得算法整体优化性能得到了大幅度的提高。

通过求解6个平移和旋转函数以检验ILFPSO解决复杂优化问题的能力，结果如表4所示。从表4可以看出，在求解函数f24、f25、f27、f28时，在Max、Min、Mean和Std上，ILFPSO均优于其他3种对比算法；在求解函数f23时，ELPSO表现出了最佳的寻优能力，ILFPSO稍差；而在求解f26时，在Max、Min和Mean上，ILFPSO最佳。相对于LFPSO，在所有的6个复杂函数f23～f28上，ILFPSO表现更优。这说明ILFPSO解决复杂优化问题的能力具有较强的竞争力。

综上所述，本文提出的ILFPSO算法在28个benchmark函数中的25个函数上都获得了最优的性能，充分证明了ILFPSO的普适性较强。虽然对于求解个别benchmark函数仍存在相对较差的性能，但在求解所有28个benchmark函数上，ILFPSO优于LFPSO，整体上说明本文提出的3点改进可行。

3.3 收敛性分析

为更清晰地看出ILFPSO算法的收敛性能，实验给出了4种算法在求解所有函数时的收敛曲线图，如图3所示。因版面限制，只从4类benchmark函数中选取6个函数进行展示，将平均适应度值(对于函数f25，每次的结果减去Fmin再进行平均)作为评估算法性能的主要参考值，测试迭代次数为2 500时算法的收敛性能。

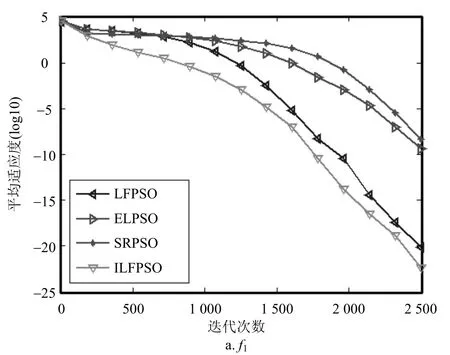
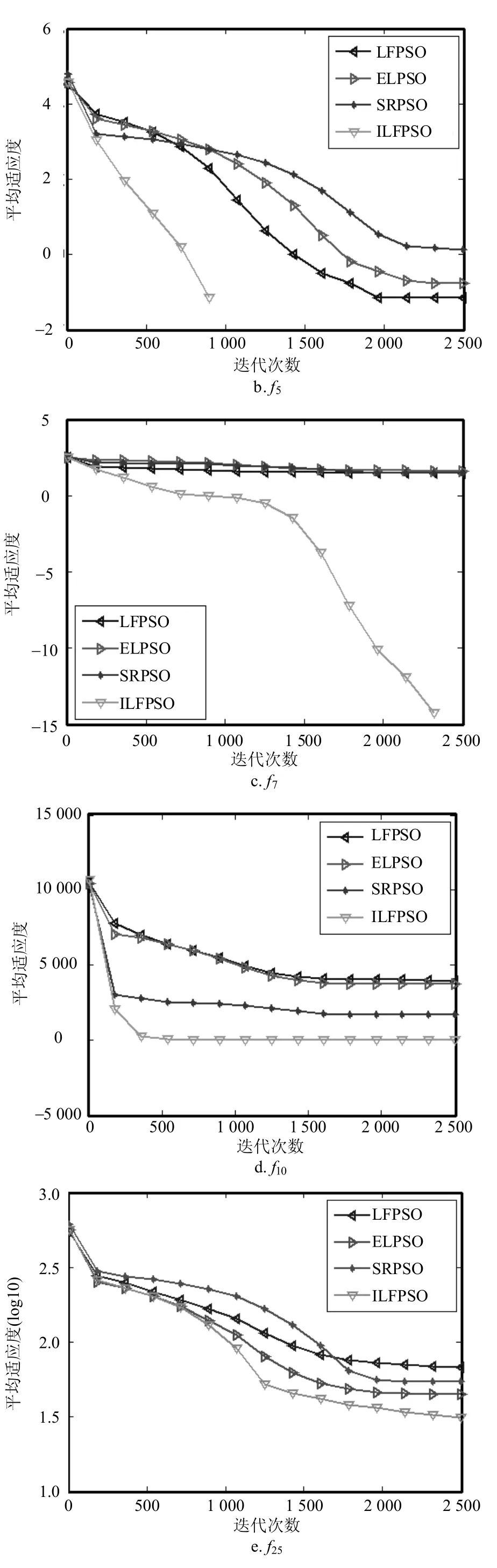
图3 4种算法在4类benchmark函数上的收敛曲线图

从图3可以看出，ILFPSO在对f5、f7、f27等函数进行优化时收敛速度大幅度优于其他3种对比算法；而针对f1、f10、f25等函数，ILFPSO收敛性能也明显优于其他对比算法。另外，虽然ILFPSO在优化f21、f23等函数时收敛性能稍差，ELPSO最好，但ILFPSO紧跟其后，排在第2位。从整体情况来看，ILFPSO在28个函数上的收敛性能都优于LFPSO，这些再一次证明ILFPSO的改进策略是有效的。

3.4 运行时间对比

4种优化算法的运行时间结果如表5所示。从表5可以看出，当求解单峰函数f1～f6、f19时，ELPSO的运行速度最快，ILFPSO的运行速度次之，但ILFPSO大幅度领先另外2种对比算法LFPSO和SRPSO。

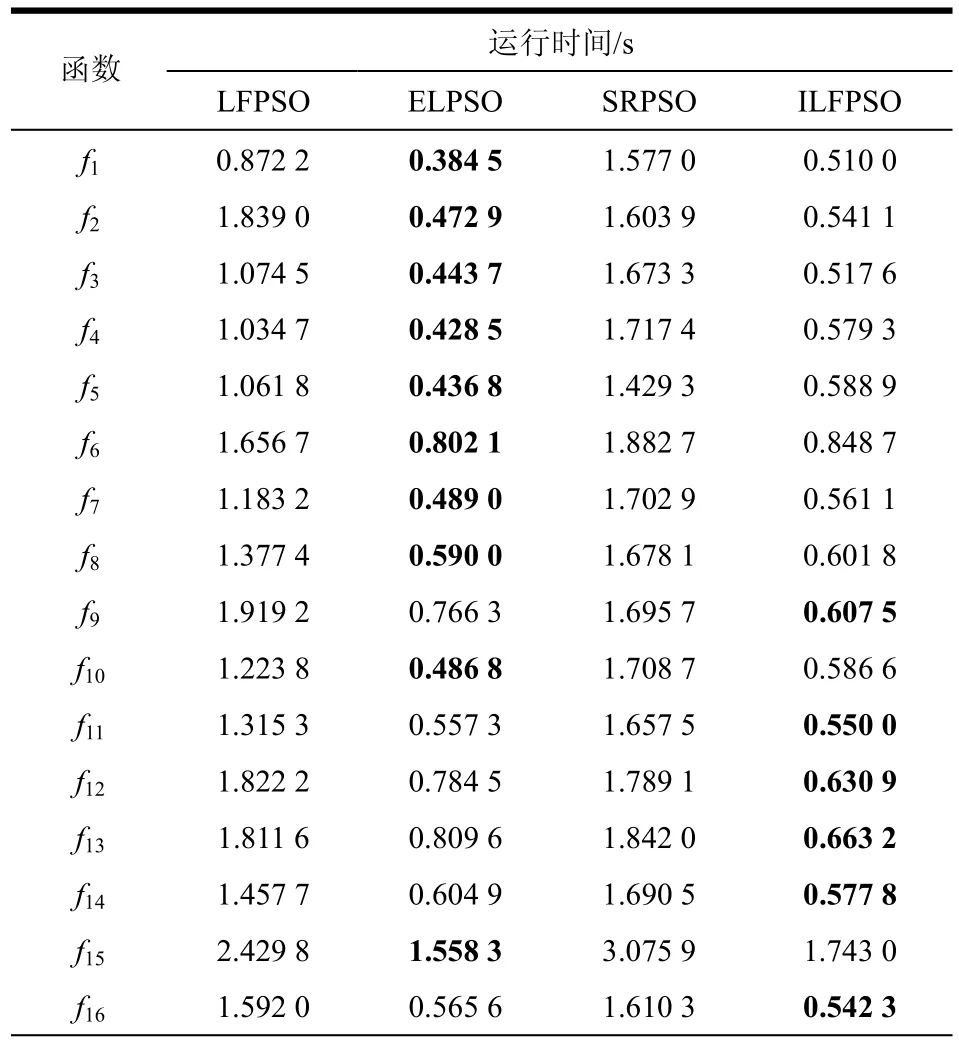
表5 4种优化算法运行时间对比

续表

在求解多峰函数f7、f8、f10、f15、f17、f18、f21和f22时，ELPSO运行速度最快，而求解f9、f11～f14、f16和f20时，ILFPSO运行速度最快；当求解平移和旋转函数f23～f25和f27时，ILFPSO耗时最少，求解旋转函数f26和f28时，ELPSO耗时最少，但二者相差不大。从表5最后一行看，ILFPSO的平均运行时间是0.833 5 s，是4种算法中耗时最少的，约为LFPSO(1.797 7 s)的50%，其主要原因见3.5节计算复杂度分析。

3.5 复杂度分析

一般来讲，一个优化算法的计算复杂度由两部分组成：目标函数的计算复杂度和优化算法自身的计算复杂度，本文重点分析ILFPSO与LFPSO计算复杂度。因为两种算法的目标函数评价次数相同，目标函数的计算复杂度相同，所以在此仅分析两种算法自身的复杂度。LFPSO中Levy Flight算子的计算复杂度高，当嵌入计算复杂度较低的趋优算子时，两个算子交替运行，如此降低了ILFPSO的整体计算复杂度。另外，ILFPSO消除无效解也在一定程度上提高了算法的计算效率。

3.6 ILFPSO与RLPSO的性能对比

为进一步说明ILFPSO算法的寻优能力，选取f1、f3、f7、f9、f11、f19作为测试函数。将ILFPSO算法与国内目前最优秀的具有反向学习和局部学习能力的PSO算法(RLPSO)[2]进行对比。两种算法的参数：维数n为30，种群数量为20。两种算法的实验数据如表6所示，RLPSO的实验数据直接来自文献[2]。

从表6可以看出，不管是Mean还是Std，ILFPSO大幅度优于RLPSO，说明ILFPSO全局搜索能力更好，收敛速度更快以及收敛精度更高，而且对比实验中本文提出ILFPSO的最大目标函数评价次数(maxEFs)比RLPSO少得多，前者为5×104，后者为1×105，这更说明ILFPSO比RLPSO优化性能好。

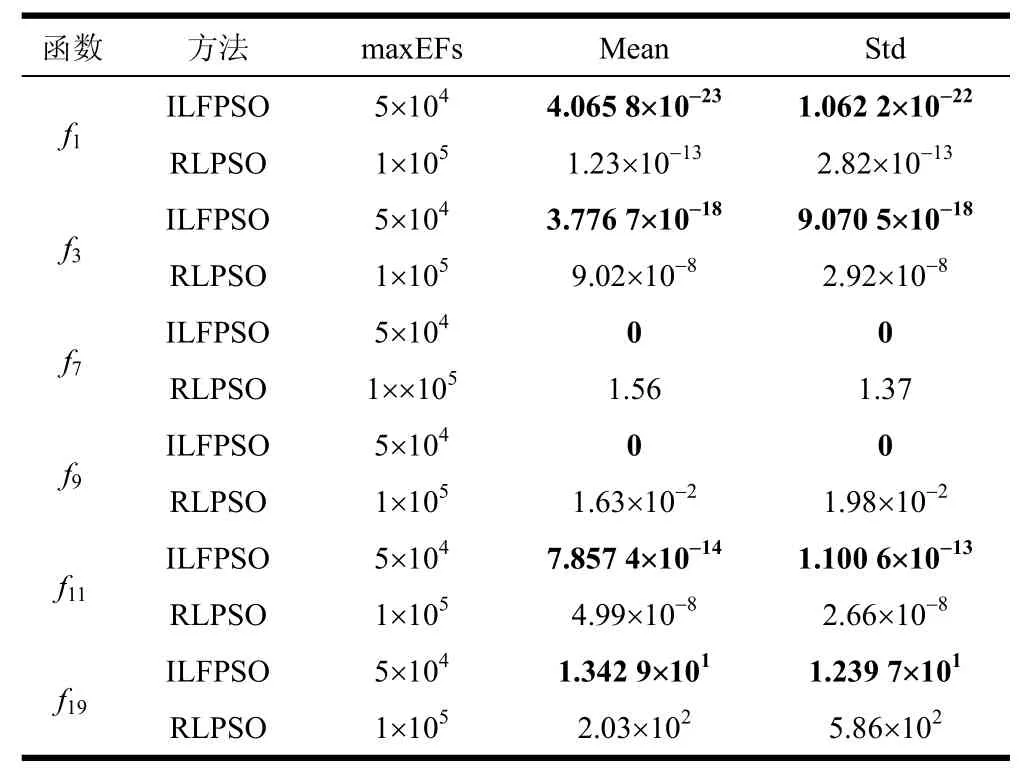
表6 ILFPSO与RLPSO算法的结果对比

通过以上仿真实验及结果对比，ILFPSO很好地避免了LFPSO中出现的收敛速度慢、易产生无效解、搜索效率不高以及普适性不强等问题。这些问题的解决主要因为：

1) ILFPSO为平衡原始算法的全局和局部搜索能力以及加快算法的收敛速度而引进了趋优算子；

2) 对速度的边界进行动态更新，提高了ILFPSO的前期全局搜索能力和后期局部搜索能力；

3) 改进的Levy Flight算子避免出现无效解。因此，与LFPSO、ELPSO、SRPSO和RLPSO相比，ILFPSO具有更高的优化效率，更好的普适性。

4 结束语

针对LFPSO中出现的搜索效率不高和普适性不强等问题，本文提出了一种趋优算子与Levy Flight混合的粒子群优化算法。首先改进Levy Flight算子，解决了LFPSO中易产生无效解的问题。然后控制趋优算子与Levy Flight的交替运行，更好地平衡了算法的全局与局部搜索能力，提高了算法的普适性。最后在每次迭代时对速度的边界进行动态更新，用于提高前期全局搜索能力和后期局部搜索能力。28个benchmark函数仿真实验结果表明本文提出的方法是有效的，与当前最优秀的PSO改进算法相比，ILFPSO更具有竞争性和普适性。

[1]张新明, 涂强, 尹欣欣, 等. 嵌入趋化算子的PSO算法及其在多阈值分割中的应用[J]. 计算机科学, 2016, 43(2)：311-315.ZHANG Xin-ming, TU Qiang, YIN Xin-xin, et al.Chemotaxis operator embedded particle swarm optimization algorithm and its application to multilevel thresholding[J].Computer Science, 2016, 43(2)： 311-315.

[2]夏学文, 刘经南, 高柯夫, 等. 具备反向学习和局部学习能力的粒子群算法[J]. 计算机学报, 2015, 38(7)：1397-1407.XIA Xue-wen, LIU Jing-nan, GAO Ke-fu, et al. Partucle swarm optimization algorithm with reverse-learning and local-learning behavior[J]. Chinese Journal of Computers,2015, 38(7)： 1397-1407.

[3]LIM W H, ISA N A M. Adaptive division of labor particle swarm optimization[J]. Expert System with Application,2015, 42(14)： 5887-5903.

[4]TANWEER M R, SURESH S, SUNDARARAJAN N. Self regulating particle swarm optimization algorithm[J].Information Science, 2015, 294： 182-202.

[5]JORDEHI A R. Enhanced leader PSO (ELPSO)： a new PSO variant for solving global optimization problems[J]. Applied Soft Computing, 2015, 26： 401-417.

[6]HAKLI H, UGUZ H. A novel particle swarm optimization algorithm with Levy Flight[J]. Applied Soft Computing,2014, 23： 333-345.

[7]倪庆剑, 邓建明, 邢汉承. 基于异构多种群策略的动态概率粒子群优化算法[J]. 模式识别与人工智能, 2014, 27(2)：146-152.NI Qing-jian, DENG Jian-ming, XING Han-cheng.Dynamic probabilistic particle swarm optimization based on heterogeneous Multiple population strategy[J]. Pattern Recognition and Artificial Intelligence, 2014, 27(2)：146-152.

[8]艾兵, 董明刚. 基于高斯扰动和自然选择的改进粒子群优化算法[J]. 计算机应用, 2016, 36(3)： 687-691.AI Bing, DONG Ming-gang. Improved particle swarm optimization algorithm based on Gaussian disturbance and natural selection[J]. Journal of Computer Applications, 2016,36(3)： 687-691.

[9]ZHANG W, LIU J, FAN L B, et al. Control strategy PSO[J].Applied Soft Computing, 2016, 38： 75-86.

[10]TAHERKHANI M, SAFABAKHSH R. A novel stabilitybased adaptive inertia weight for particle swarm optimization[J]. Applied Soft Computing, 2016, 38：281-295.

[11]OMRAM M G H, MAHDAVI M. Global-best harmony search[J]. Applied Mathematics and Computation, 2008,198(2)： 643-656.

[12]李景阳, 王勇, 李春雷. 采用双模飞行的粒子群优化算法[J]. 模式识别与人工智能, 2014, 27(6)： 533-539.LI Jing-yang, WANG Yong, LI Chun-lei. Particle swarm optimization algorithm with double-flight modes[J].Pattern Recognition and Artificial Intelligence, 2014, 27(6)：533-539.

[13]KIRAN M S, HAKLI H, GUNDUZ M, et al. Artificial bee colony algorithm with variable search strategy for continuous optimization[J]. Information Science, 2015, 300：140-157.