基于离散粒子群优化的鲁棒Web服务组合
叶恒舟,陆湘鹏
(桂林理工大学嵌入式技术与智能信息处理广西高校重点实验室 广西 桂林 541006)
Web服务已深入应用于实现面向服务的计算(service-oriented computing, SOC)和面向服务的构架(service-oriented architecture, SOA)[1]。随着Web服务技术的发展,单个Web服务往往难以满足人们日益增长的需要。Web服务组合将多个Web服务组合成满足用户需求的复合服务,使其具有更强大的功能。服务质量(quality of service, QoS)用于区别功能相同的Web服务的非功能属性,如何从众多服务中选择满足用户需求,且具有最优QoS的组合服务,即QoS感知的Web服务组合(QSC)问题,是当前的研究热点。
目前已经有很多求解QSC问题的方法[2-3],它们均假定了服务的QoS不随时间变化,即取某个确定值。然而,由于Web服务环境的动态性,服务的QoS属性具有内在的不确定性[4-5],因而有必要研究QoS不确定时的服务组合问题。文献[6]采用云模型计算QoS的不确定性,剔除冗余服务。文献[7]提出一种p-R-tree索引结构和一种双重剪枝方案计算p-dominant skyline,从而降低候选服务及其组合的数量。文献[8]提出了一种发现可行Web服务的方法,该方法运用了随机优势理论,不关心QoS的分布情况。文献[9]也采用了随机优势理论剔除不满足约束的解,准确性更好。这些研究只是淘汰了部分候选服务,并不能直接获得最优组合服务,且仅考虑了顺序结构的工作流。
为了增强服务组合时,对动态环境的适应性,一些文献采用云模型[10]或历史事务信息[11]等方式更精确地估计QoS属性值,或者采用了即时推荐策略[12]或约束分解策略[13]。少量文献则在服务组合时,考虑了其鲁棒性能。文献[14]考虑了传感网络具有的不可靠性和不稳定性,提出了一种新的服务模型和动态选择方法,但不适用于基于因特网的服务组合场景。文献[15]所提出的鲁棒服务组合方法,目标是扩大所选择的服务簇在网络空间上的覆盖范围,以降低局部网络异常带来的影响。文献[16]仅考虑了响应时间的不确定性,而文献[17]仅考虑了执行价格的不确定性。
本文假设候选服务的QoS属性值及其聚合服从正态分布,通过估计两个正态分布的和、积、最大、最小、平均值的期望与方差,建立了一种鲁棒服务组合优化模型。与上述研究工作不同,该模型可以支持执行价格、响应时间、可靠性、成功率等QoS属性的不确定性,也可以支持由顺序、选择与并发模式经过有限次嵌套而生成的任意工作流。
1 鲁棒Web服务组合模型
Web服务组合的一个研究热点是,对于给定的工作流,为该工作流中的每个任务挑选一个合适的候选服务,使最终的组合服务在满足用户给定的某些QoS属性约束的同时,优化由用户所关注的另外一些QoS属性所确定的综合效用。本文所考虑的鲁棒Web服务组合问题是在此基础上,考虑候选服务QoS属性值的不确定性,并使最终的组合服务具备较好的鲁棒性。
设工作流F包含N个任务,任务有Mi个候选服务,为F的解域。候选服务涉及K个QoS属性。服务的QoS属性往往既有增益性的,也有减益性的,但两者很容易相互转换,本文假设qij涉及的QoS属性都是增益性的。在考虑QoS属性值的不确定性时,比较常见的是认为QoS属性值服从正态分布,设服从正态分布
不失一般性,设k= 1, 2,…,r- 1(1≤r≤K)是用户所关心的效用属性,k=r,r+ 1,…,K是用户所关心的约束属性;对于某个组合服务s∈D(F),qk(s)表示其第k(k= 1, 2,…,K)个QoS属性的聚合值。鲁棒Web服务组合问题(RWSC)模型可以表示为:
目标:
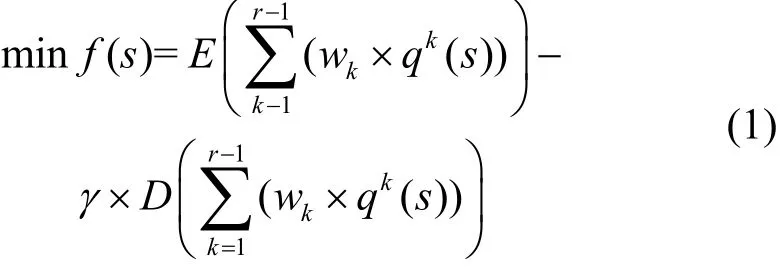
约束条件:
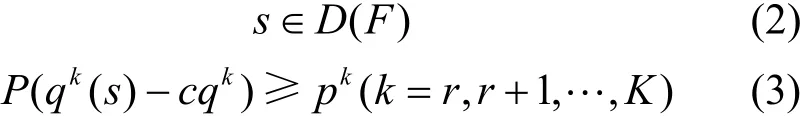
式(1)给出了优化目标,即选择使用户所关心的效用QoS属性的聚合值的加权平均的期望最大化,方差最小化的组合服务,其中E(X)、D(X)表示X的期望与均方差,γ≥0为可调参数,wk为第k个QoS属性的权值,满足0 ≤wk≤ 1 (k=1, 2,…,r-1)且;式(2)限制了s的取值范围;式(3)描述了用户所关心的约束条件,P(X)表示事件X发生的概率,cqk(k=r,r+1,…,K)为用户给定的约束限,pk为用户给定的概率约束值或者取经验值,如根据“3σ”法则,并假设qk(s)服从正态分布,可取pk=99.74%,此时,式(3)等价于式(4)。
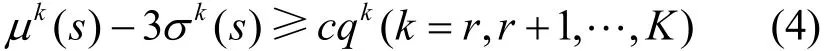
式中,μk(s)、σk(s)分别为qk(s)的期望与均方差。
2 组合服务的QoS聚合
具体化RWSC模型的关键是确定组合服务的QoS属性的聚合值,即的计算方法。很多文献[2,18-20]针对QoS属性为确定数值的情况进行了研究,核心是确定工作流F中常见顺序、选择及并发等模式的QoS聚合规则。当QoS属性服从正态分布时,这些规则仍然是可以借鉴的,即可根据表1计算各种模式下的QoS属性聚合值,其中Xi(i=1, 2,…,n)表示第i个服务的某个QoS属性所对应的随机变量。
从表1可以看出,计算涉及到n个随机变量的累加、最大值、最小值及累积等运算。考虑到这几种运算都具备交换律与结合律,且各个候选服务都具备独立性,并认为两个正态分布的上述运算结果近似符合正态分布,可以仅考虑两个相互独立的正态随机变量的和、最大值、最小值及积的计算方法。
2.1 两个正态分布的和
设X1、X2是两个正态分布随机变量,
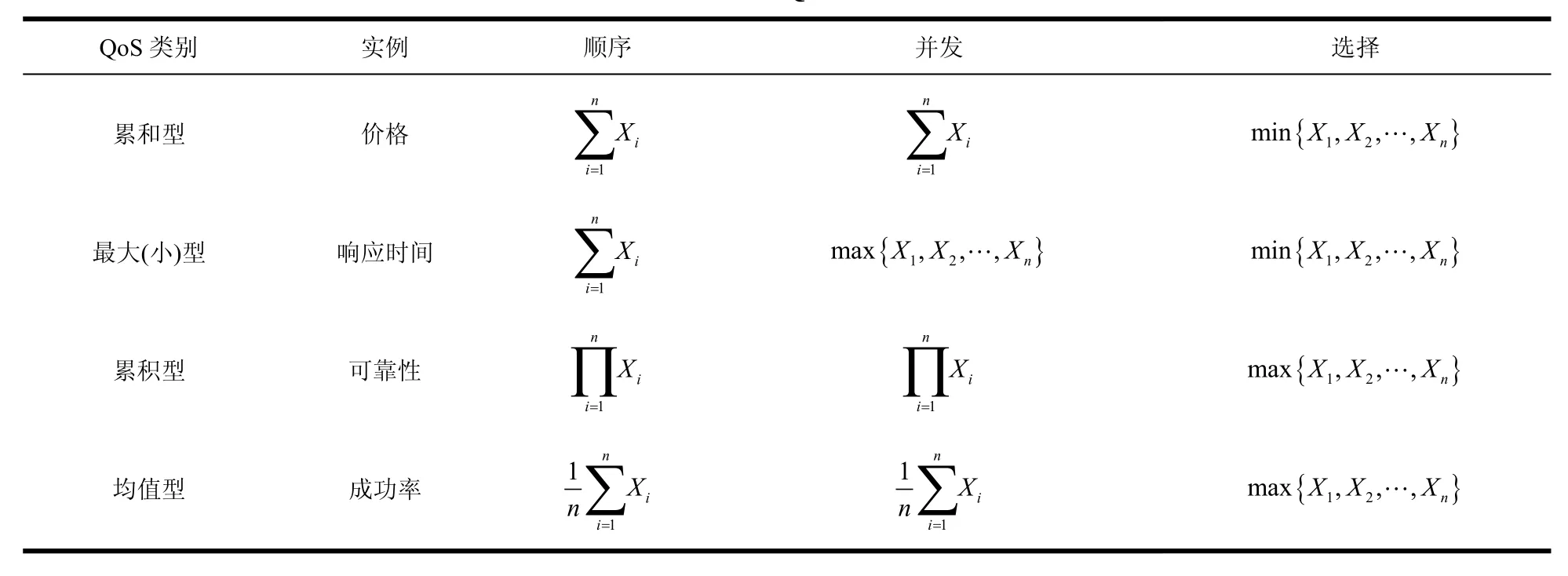
表1 不同模式下各QoS属性的聚合规则
2.2 两个正态分布的最大值
记Y= max(X1,X2),设μ1≤μ2,根据“3σ”法则,Y的分布存在图1所示的3种可能,其中d1=(μ1-μ2) - 3 (σ1-σ2),d2= (μ1-μ2) + 3 (σ1-σ2)。
对于图1a,Y主要分布在区域 [μ1-3σ1,μ2+3σ2]上;对于图1b,Y主要分布在区域[μ2- 3σ2,μ1+ 3σ1]上;对于图1c,Y主要分布在区域[μ2- 3σ2,μ2+ 3σ2]上。若认为Y近似于服从正态分布,可得式(5)和式(6)。
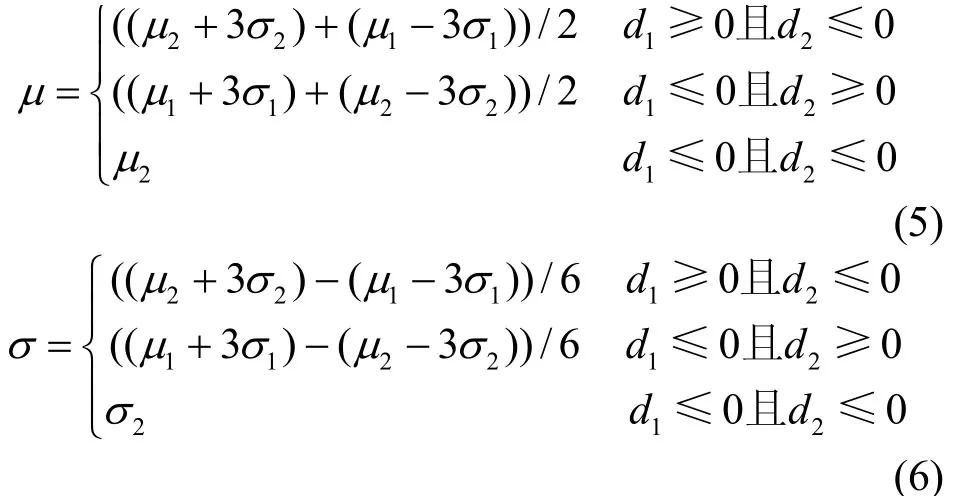
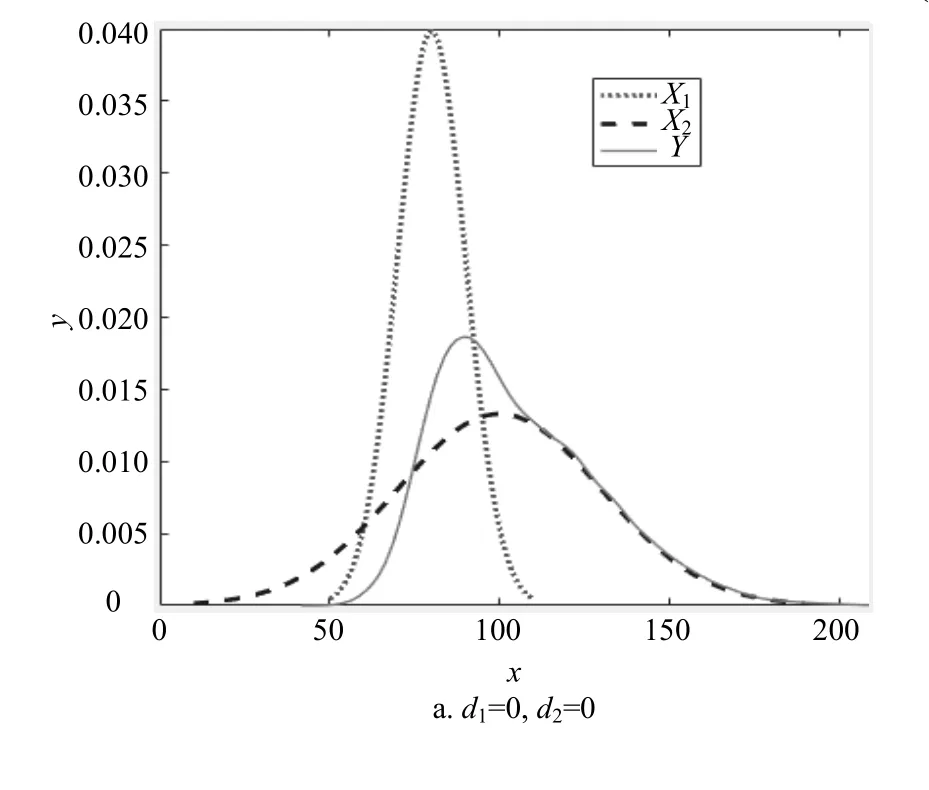


图1Y的3种可能分布
2.3 两个正态分布的最小值
记Y= min(X1,X2),设μ1≤μ2,类似2.2节的分析可得,Y近似于服从正态分布N(μ,σ2) ,可得式(7)和式(8)。
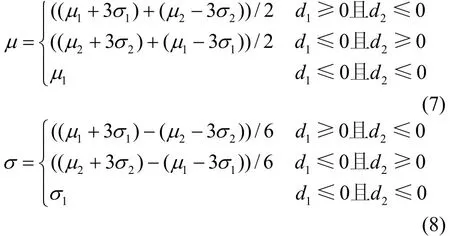
2.4 两个正态分布的积
记Y=X1×X2,则Y的期望E(Y)及方差D(Y)可以分别由式(9)、(10)计算,因此可以认为Y近似服从正态分布N(E(Y),D(Y))。
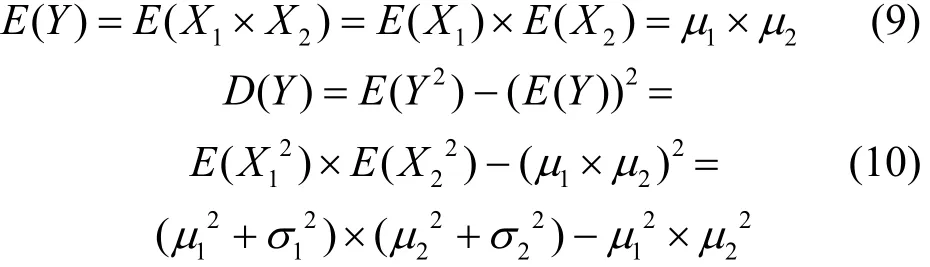
3 求解RWSC的DPSO算法
3.1 粒子的位置与速度
设第i个粒子的位置Xi= <xi1,xi2,…,xiN>,其中xij(j= 1, 2,…,N)为一个正整数,表示为任务tj选择的候选服务的编号(从1开始编号)。显然,Xi对应于某个服务s∈D(F)。第i个粒子的速度记为Vi=<Vi1,Vi2,…,ViN>,vij(j= 1, 2,…,N)表示服务sjxkj的综合效用;服务sij的综合效用f(sij),由式(11)确定。

式中,r、wk、E(·)、D(·)、γ与式(1)一致;qk(s)表ij示服务sij的第k个QoS属性值。
3.2 粒子的速度与位置更新公式
参照PSO算法中对粒子的速度与位置的定义,可得粒子的速度和位置的离散迭代如下:
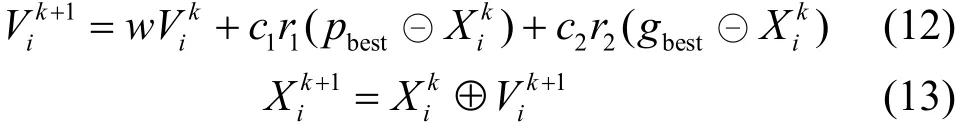
式中,w为惯性权重,在[0,1]区间取值;c1和c2是学习因子,可取值为2;r1和r2是在区间[0, 1]上取值的随机数;k表示当前的迭代次数。算子⊖和⊕分别由式(14)、式(15)定义。⊖度量两个粒子各个维度上的效用差,而⊕为粒子的各个维度选择一个新的位置,使该位置所代表的候选服务的综合效用与原位置的效用加上速度后的值最为接近。
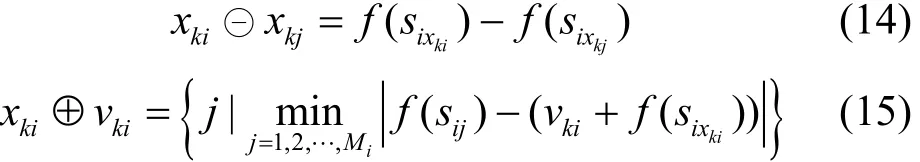
3.3 粒子的适应度函数
设粒子Xi对应服务s,粒子Xi的适应度U(s)可由式(16)计算,其中 ()k gs用于判断s对于第k个QoS属性的违约情形,由式(17)度量。式(16)表明,当s满足约束条件时,Xi适应度为f(s);当s不满足约束条件时,Xi适应度会在f(s)基础上有所降低,降低的幅度与违反约束条件的个数与程度有关,个数越多,程度越强,降低幅度越大。β>0为可调系数。

3.4 DPSO算法步骤

4 实验分析
4.1 实验场景
实验时选取了4种规模的服务组合问题,其任务个数N与候选服务个数M分别为(20, 100)、(20, 400)、(200, 100)、(200, 400),每种规模的相关实验测试40次取平均值。实验所用工作流依问题规模随机产生,其中顺序、选择、并发模式的占比分别为1/2、1/4、1/4。考虑执行价格、响应时间、可靠性、成功率4种QoS属性,其中执行价格为优化目标,响应时间、可靠性、成功率为约束条件。执行价格的期望在[100,1 000]上随机取值,其他QoS属性的期望从QWS Dataset V2开放数据集[21-22]中取值;各QoS属性的均方差为其期望的a倍,a分别在区间[0.1, 0.2]、[0.1,0.2]、[0.001, 0.005]和[0.05, 0.1]上取随机值。相关差数取值为:γ= 0;β= 2;w= 0.6 - 0.4t/T(t和T分别为当前迭代次数和总迭代次数)。编程语言为Java 1.6。
4.2 鲁棒性测试
采用类似文献[23]所定义的鲁棒概率(robustness probability)评价所求得的组合服务的鲁棒性。鲁棒概率Rp,表征组合服务满足用户约束的概率,可由式(18)计算,其中TotalTimes、failedTimes分别表示测试的总次数、违反用户约束的次数。
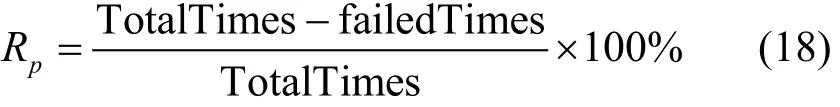
表2显示了不同问题规模时,依据所建立的优化模型,采用DPSO所选择的组合服务的平均鲁棒概率(TotalTimes取值为10 000)。测试结果表明,所选择的组合服务具有很好的鲁棒性,且基本不受问题规模的影响。
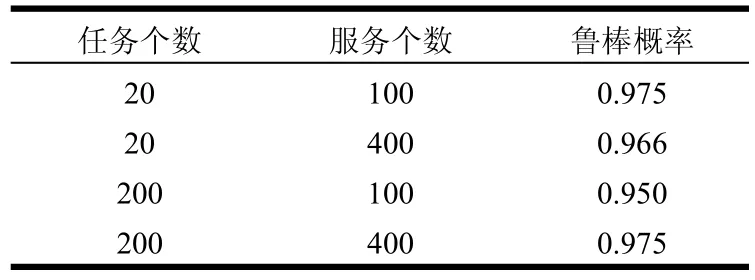
表2 组合服务的平均鲁棒概率
4.3 模型精度测试
所建立的优化模型中,组合服务的QoS属性聚合值的期望与均方差有些是近似计算的,有必要测试其粒度。测试时,针对某个组合服务问题,随机生成一个组合服务,分别为优化模型的计算方法及采样(样本总数为10 000)计算方式获取该组合服务的响应时间、可靠性及成功率的期望与均方差,比较两者的相对偏差,即模型计算值与采样计算值之差与采样计算值的比值。
表3给出了不同问题规模时,组合服务各QoS属性聚合值的期望与均方差的相对偏差值。分析这些数据,可以发现:1) 各QoS属性的聚合值的期望的偏差不超过0.2%,精度相当高;2) 响应时间与可靠性的均方差的偏差约2%,与问题规模无明显关联;3) 成功率的均方差的偏差较高,且随任务个数增加,这在一定程度上是因为成功率的属性值的期望值中有一些取值为1或很接近1,加上波动后往往大于1,而测试时约定成功率不能大于1。总的来看,由模型计算的组合服务的各QoS属性的聚合值的期望与方差与真实值的偏差不大,精度较好。
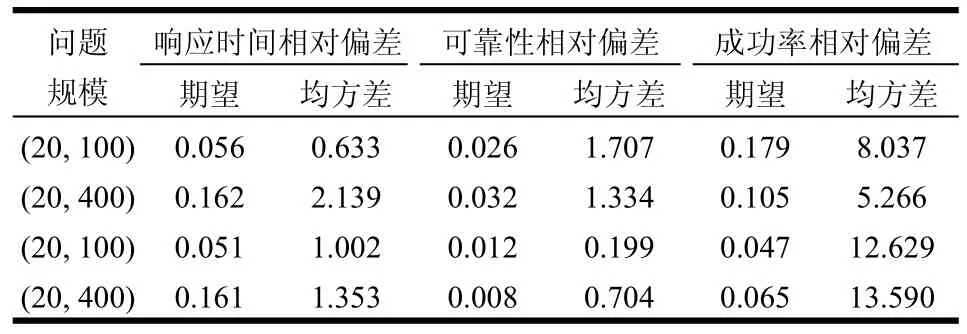
表3 组合服务各QoS属性期望与均方差的相对偏差 %
5 结束语
应用于互联网的Web服务的QoS受到很多因素的影响,很难准确估计其属性值。鲁棒Web服务组合方法,意在当服务的QoS在一定范围内波动时,所选择的组合服务仍能在很大程度上满足用户的约束条件。通过给出各种QoS聚合计算方法,提出了一种鲁棒Web服务组合优化模型,并采用了一种支持约束条件的离散粒子群优化算法求解该模型。模型仅考虑了服务的QoS服从正态分布的情形,模型的精度,特别是均方差的计算精度还有待改进。
[1]WANG Peng-wei, DING Zhi-jun, JIANG Chang-jun, et al.Automatic web service composition based on uncertainty execution effects[J]. IEEE Transactions on Services Computing, 2016, 9(4): 551-565.
[2]LIU Zhi-zhong, CHU Dian-hui, SONG Cheng, et al. Social learning optimization (SLO) algorithm paradigm and its application in QoS-aware cloud service composition[J].Information Sciences, 2016, 326: 315-333.
[3]CHEN Ying, HUANG Ji-wei, LIN Chuang, et al. A partial selection methodology for efficient QoS-aware service composition[J]. IEEE Transactions on Services Computing,2015, 8(3): 384-397.
[4]ZHENG Zi-bin, ZHANG Yi-lei, LYU M R. Investigating QoS of real-world web services[J]. IEEE Transactions on Services Computing, 2014, 7(1): 32-39.
[5]ROSARIO S, BENVENISTE A, HAAR S, et al.Probabilistic qos and soft contracts for transaction-based web services orchestrations[J]. IEEE Transactions on Services Computing, 2008, 1(4): 187-200.
[6]王尚广, 孙其博, 张光卫, 等. 基于云模型的不确定性QoS感知的Skyline服务选择[J]. 软件学报, 2012, 23(6):1397-1412.WANG Shang-guang, SUN Qi-bo, ZHANG Guang-wei, et al. QoS-aware skyline service selection based on cloud model[J]. Journal of Software, 2012, 23(6):1397-1412.
[7]YU Q, BOUGUETTAYA A. Computing service skyline from uncertain QoWS[J]. IEEE Transactions on Services Computing, 2010, 3(1): 16-29.
[8]FU Xiao-dong, YUE Kun, LIU Li, et al. Discovering admissible Web services with uncertain QoS[J]. Frontiers of Computer Science, 2015, 9(2): 265-279.
[9]付晓东, 岳昆, 刘骊, 等. 不确定服务质量感知的Web服务可行组合方案计算[J]. 计算机集成制造系统, 2016,22(1): 122-132.FU Xiao-dong, YUE Kun, LIU Li, et al. Admissible composition plans of Web services with uncertain QoS[J].Computer Integrated Manufacturing Systems, 2016, 22(1):122-132.
[10]申利民, 陈真, 李峰. 一种考虑QoS数据不确定性的服务选取方法[J]. 计算机集成制造系统, 2013, 19(10):2652-2663.SHEN Li-min, CHEN Zhen, LI Feng. Service selection approach considering the uncertainty of QoS data[J].Computer Integrated Manufacturing Systems, 2013, 19(10): 2652-2663.
[11]KIL H, CHA R, NAM W. Transaction history-based web service composition for uncertain QoS[J]. International Journal Of Web And Grid Services, 2016, 12(1): 42-62.
[12]CHELLAMMAL S, GOPINATH G, MANIKANDAN S R.An approach for selecting best available services through a new method of decomposing QoS constraints[J]. Service Oriented Computing and Applications, 2015, 9(2):107-138.
[13]CHEN Liang, WU Jian, JIAN Heng-yi, et al. Instant recommendation for web services composition[J]. IEEE Transactions on Services Computing, 2014, 7(4): 586-598.
[14]GEYIK S C, SZYMANSKI B K, ZERFOS P. Robust dynamic service composition in sensor networks[J]. IEEE Transactions on Services Computing, 2013, 6(4): 560-572.
[15]WAGNER F, ISHIKAWA F, HONIDEN S. Robust service compositions with functional and location diversity[J].IEEE Transactions on Services Computing, 2016, 9(2):277-290.
[16]DU Yan-hua, TAN Wei, ZHOU Meng-chu. Timed Compatibility analysis of web service composition: a modular approach based on petri nets[J]. IEEE Transactions on Automation Science And Engineering,2014, 11(2): 594-606.
[17]MARKOU G, REFANIDIS I. Cost-sensitive probabilistic contingent planning for web service composition[J].International Journal on Artificial Intelligence Tools, 2016,25(1): 21.
[18]马文龙, 王铮, 赵燕伟. 基于改进蚁群算法的制造云服务组合优化[J]. 计算机集成制造系统, 2016, 22(1): 113-121.MA Wen-long, WANG Zheng, ZHAO Yan-wei. Optimizing services composition in cloud manufacturing based on improved ant colony algorithm[J]. Computer Integrated Manufacturing Systems, 2016, 22(1): 113-121.
[19]张以文, 吴金涛, 赵姝, 等. 基于改进烟花算法的Web服务组合优化[J]. 计算机集成制造系统, 2016, 22(2): 422-432.ZHANG Yi-wen, WU Jin-tao, ZHAO Shu, et al.Optimization service composition based on improved firework algorithm[J]. Computer Integrated Manufacturing Systems, 2016, 22(2): 422-432.
[20]张燕平, 荆紫慧, 张以文, 等. 基于离散粒子群算法的动态Web服务组合[J]. 计算机科学, 2015, 42(6): 71-75.ZHANG Yan-ping, JING Zi-hui, ZHANG Yi-wen, et al.Dynamic web service composition based on discrete particle swarm optimization[J]. Computer Science, 2015,42(6): 71-75.
[21]AL-MASRI E, MAHMOUD Q H. Discovering the best web service[C]//Proceedings of the 16th International Conference on World Wide Web (WWW). New York,USA: ACM, 2007: 1257-1258.
[22]AL-MASRI E, MAHMOUD Q H. QoS-based discovery and ranking of web services[C]//Proceedings of 16th International Conference on Computer Communications and Networks, (ICCCN). Honolulu, HI: IEEE Computer Society, 2007: 529-534.
[23]RAMACHER R, MONCH L. Robust multi-criteria service composition in information systems[J]. Business &Information Systems Engineering, 2014, 6(3): 141-151.

