城市公交网络运行演化分析与瓶颈甄别

王 璞，谭 倩，徐仲之，鲁恒宇，林 涛

(1. 中南大学交通运输工程学院 长沙 410075；2. 深圳市城市交通规划设计研究中心 广东 深圳 518021)

大力发展公共交通，是缓解交通拥堵的重要手段，然而目前我国大城市的公交出行率仅有30%，提高市民的公交使用率已成为一个亟需解决的问题。城市公交出行率的提升不仅取决于道路、车辆等硬件设施的升级，更依赖于先进的公交运营管理技术。传统公交运营优化大多依靠由人力采集的客流数据，具有成本大、周期长、不准确等缺点。随着公交IC卡在我国各大城市的迅速推广，以及GPS数据采集与分析技术的普遍应用，基于大数据分析的公交客流分析成为了一个新兴的热点研究方向。由于公交IC卡及公交GPS设备采集的数据信息远比传统的客流调查准确、全面，如果能对这些大数据合理运用，不仅可以改变传统的建模求解思路，还有望建立更加智能化的调度系统及平台[1]。

目前国内外对公交网络运行速度与服务水平改善方面的研究主要侧重于3个方面：1) 现状路网拥堵路段有条件地设置公交专用道、港湾式停靠站、采取交叉口信号优先拓宽道路等手段提高通行能力[2-3]；2) 单条公交线路通过公交调度优化提高其服务水平，以达到提升整个网络服务水平的目的，如动态或实时的公交调度方法等[4-6]；3) 对公交运行服务水平评价，如基于顾客满意度的评价等[7]，但需借助问卷调查等数据采集方式。分析公交系统运行状态，优化公交系统的服务水平，需要公交网络与公交运行海量数据的支撑，此前由于大数据比较缺乏，这方面的研究还比较有限。近期，有学者对交通网络的动态特性及其自由流与拥堵状态开展了相关的研究[8-12]，但侧重点在于城市各种交通方式的混合交通流，鲜有对公交网络的演变过程即畅通状况到拥堵状况的演变过程进行研究。受到文献[8]提出的城市道路网络动态瓶颈路段识别方法的启发，本文基于海量公交车GPS数据，分析多周期下的公交网络运行状态，采用渗流理论识别网络瓶颈路段，分析公交网络在不同时间与区域的演变过程，为提高公交运行网络整体运行效率提供有效途径。

1 数据描述与数据处理

1.1 公交车GPS数据

本文使用的公交车GPS数据由深圳市城市交通规划设计研究中心提供，包括深圳市一周连续7天(2015年12月21日至2015年12月27日，其中21日至25日为工作日，26、27日为非工作日)的全部公交运营车辆的GPS坐标记录数据。工作日平均每天的GPS记录约5 000万条，非工作日平均每天的GPS记录约3 800万条。

图1 M281线路1天的GPS数据示意图

图1对2015年12月21日(工作日)和26日(非工作日)两天的深圳公交车GPS原始数据进行了可视化，图中展示了原始GPS数据记录的坐标点和线路上的公交站点位置。

以2015年12月21日为例，对公交车GPS数据进行初步的统计分析：图2a表明公交车GPS数据记录量在空间上分布不均，呈现出罗湖区、福田区的GPS数据量分布最密，南山区次之，其他区GPS数据量较稀少的分布情况，说明罗湖区、福田区的公交网络比较发达；图2b为公交车GPS数据记录量随时间的变化，从6点至20点，GPS数据量较大，20点以后数据量开始下降，24点到次日5点公交GPS数据量处于最低水平，这与城市出行规律相符，在公交的主要运营时间段(6点至20点)，公交发车频率较高，发车线路较多。

图2 深圳公交车GPS数据记录量的时空分布

图3 深圳公交路段的速度分布

图3(横坐标为公交车辆速度值，纵坐标为出现该速度的概率)表明：10点的公交车路段上的行驶速度与18点的公交在路段上的行驶速度均存在一个峰值，而且同一天中的不同时段的速度不同，18点的公交行驶速度明显低于10点的公交行驶速度，这是由于晚高峰交通拥堵造成的。而工作日(21日)与非工作日(26日)在同一时段(18点)的公交路段速度分布情况十分相近，说明深圳的工作日和非工作日都存在类似的晚高峰公交出行。

1.2 地图匹配算法及数据处理

本文采用ST-matching算法进行公交车GPS坐标的地图匹配[13]，该算法适用于低采样频率的情况。对一条待匹配轨迹T=p1→p2→…→pn，首先计算每个轨迹点pi与其在各个路段上投影点的距离，如果距离小于80 m，则认为该路段为pi的候选匹配路段，为候选匹配点。将相邻两点之间的候选匹配点两两组合，得到轨迹T的若干条候选匹配路径，使用观测可能性和传递可能性的乘积作为空间分析函数，来衡量候选匹配路径与轨迹T的匹配程度。观测可能性的计算公式为：

式中，为 pi与其候选匹配点之间的距离。

候选匹配点之间的传递可能性计算公式为：

式中，di-1→i为pi-1和pi的直线距离；w(i-1,t)→(i,s)为和的最短路径长度。

定义空间分析函数为：

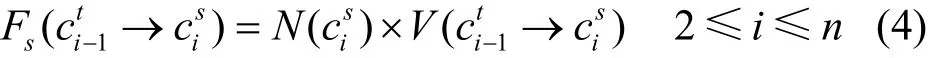
得到Pc的评估得分为：

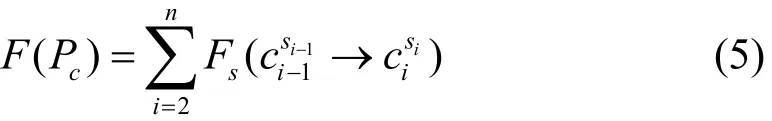
GPS轨迹T将会匹配到评估得分最高的候选匹配路径上。

公交轨迹信息为沿公交线路分布的一系列时间连续的轨迹点，由于公交运营时间的调整及公交改线往往导致轨迹点时间间隔较大、距离分布较远。基于此，考虑将轨迹按时间间隔在120 s之内、直线距离在1 500 m内拆分成连续的小轨迹，对每一条小轨迹在对应区域内完成公交GPS坐标的地图匹配。通过前后两个轨迹点的直线距离和时间间隔确定轨迹点的速度，路段速度设定为该路段上车辆行驶速度的平均值，以相邻边速度的平均值作为缺失记录边的速度值。

经过一周连续7天公交车GPS坐标匹配，仍无车辆匹配信息的路段，本文认为这些路段是非公交车运行路段，将其删去获得深圳公交网络，如图4所示。

图4 GPS数据与地图匹配结果

1.3 典型区域选取

本文选取深圳2个最典型区域的公交网络：福田区、宝安区，如图5所示。福田区位于深圳经济特区中部，是深圳的政治金融中心，轨道线网发达，交通出行需求最大，路网交通较拥堵；宝安区位于深圳市西北部，是深圳联系广州等方向的区域，以产业为主，区内基本职住平衡，路网以快速路、高速路等区域性设施为骨架，通行效率较高。各区的详细公交网络数据特征描述如下：

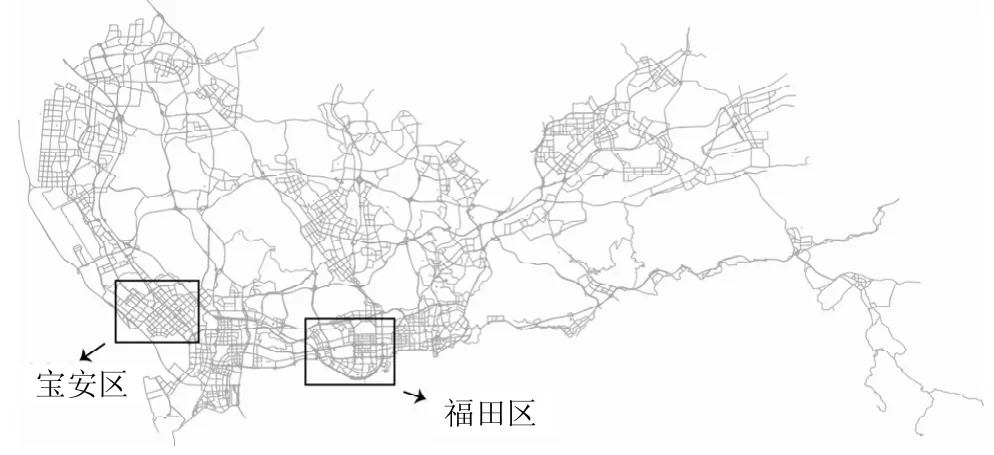
图5 选取的典型区域

福田区：区域范围约7.51 km×5.15 km，其路网由2 262条边(路段)和1 558个节点(交叉口)组成。

宝安区：区域范围约5.45 km×8.50 km，路网由918条边(路段)和605个节点(交叉口)组成。

2 基于渗流理论的公交网络运行速度演变分析

2.1 基于渗流理论的公交网络构建

渗流理论是随机图理论研究中的一个重要发现，渗流过程指网络中的边或点以某种规则逐步缺失的过程。在渗流过程中，若网络存在一个大团簇分裂成若干小团簇的现象，则称网络是可渗流的，这个过程称为渗流转变，出现渗流转变的临界点的值称为渗流阈值[14-15]。

基于渗流理论，本文设计了一种去除公交网络边的方法，构建了一个能展示公交动态运行的网络结构[16]。不同于传统公交网络拓扑结构，仅当公交运行速度值大于一个给定值的路段被认为是有效路段。为消除公交快慢线、不同道路等级的差异性，本文使用一个相对速度值来定义各路段公交运行状态。定义路段的95%位公交速度值为该路段的最大速度值，定义路段公交相对瞬时速度rij为路段公交瞬时速度与最大速度的比值。对于给定的q，路段eij可被划分为有效路段(eij=1)和无效路段(eij= 0 )。有效路段相连形成给定q值下的公交运行网络。

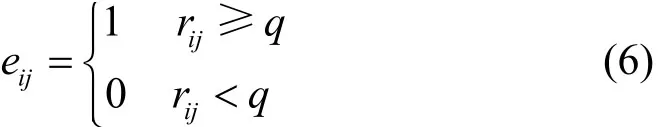
当 0q= 时，渗流公交网等同于初始公交网络，路段完全连通；当 1q=时，网络被碎片化，大部分路段孤立；当10q＞＞时，公交网络由不同大小的团簇(团簇表征公交运行相对速度大于q值的路段连接)组成。

对不同q值下最大团簇和第二大团簇进行统计分析：发现随着q值增加，构成最大团簇的有效路段数减少，而第二大团簇在某个q值下达到最大。根据渗流理论，在第二大团簇达到最大时，网络的连通性即发生渗流相变，此刻的q值应为临界阈值qc。临界阈值qc可视为标识网络连通性与运行效率的量化指标：在给定的公交网络上，qc是大部分路段(最大团簇所含路段)上能供公交车行驶的最大相对速度值。

图6、图7分别为不同q值下福田区及宝安区最大公交网络团簇及第二大公交网络团簇的分布(周一时段：10：00-11：00，实线和虚线分别代表最大公交团簇G和第二大公交团簇中的有效路段数SG)。

计算结果表明：福田区与宝安区周一10：00-11：00段的渗流阈值均为0.6，可见在该时段，不管是中心拥堵区还是非中心区，其公交网络运行效率相差无几。

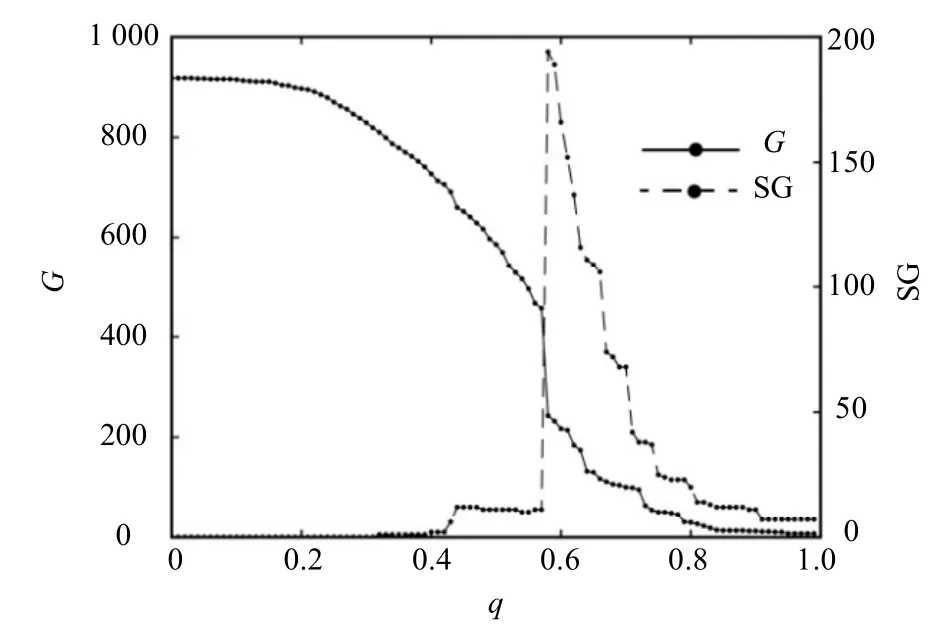
图6 不同q值下福田区最大及第二大公交网络团簇

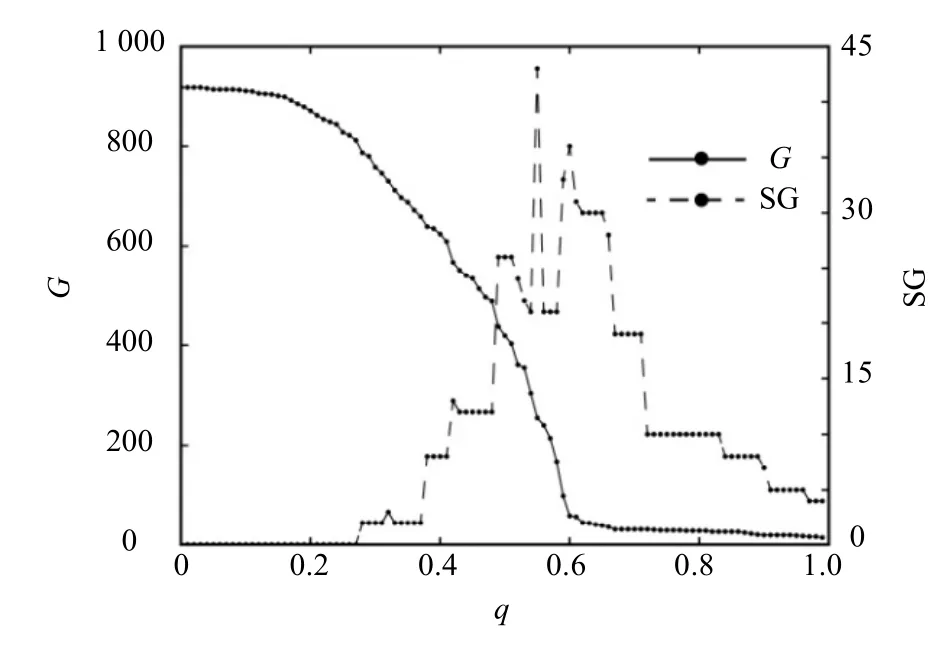
图7 不同q值下宝安区最大及第二大公交网络团簇

2.2 公交路段速度演变分析

1) 同一时段不同q值下的公交网络运行速度演变。

选择福田区与宝安区午时时段(10：00-11：00) 3种情况下(q= 0 .3，q= 0 .62，q= 0 .75)的渗流公交网络的特征进行分析。同一时段下q值不同，可表明出行者对公交网络运行速度不同的接受值，即给定的q值越小，出行者接受的公交网络运行速度值越小。

福田区：如图8所示，当q= 0 .3时，网络形成一个巨大的团簇，连通性非常好，基本与原始路网一致；当q= 0 .75时，形成几个较小的团簇，即运行速度较高的公交路段占整个路网的很小一部分，大部分路段是无效的，路网连通性很差；当q= 0 .62时，形成3个不同大小的团簇，其中第二大团簇明显比q= 0 .75和q= 0 .3时的第二大团簇要大，团簇内部连通性好，但大团簇之间缺乏联系，团簇之间存在瓶颈路段造成拥堵，影响整个公交网络的连通性。

该现象说明在出行者接受公交运行速度为其最大速度值的30%时，整个公交网络连通性好；若为其最大速度值的62%时，网络中存在某个较大的区域可满足出行者的需求，同时，若想要达到更高的运行速度，则必须找出网络瓶颈并改善。否则，公交网络能达到出行者要求的路段寥寥无几，如公交运行速度是日常最高运行速度的75%时的渗流网络。

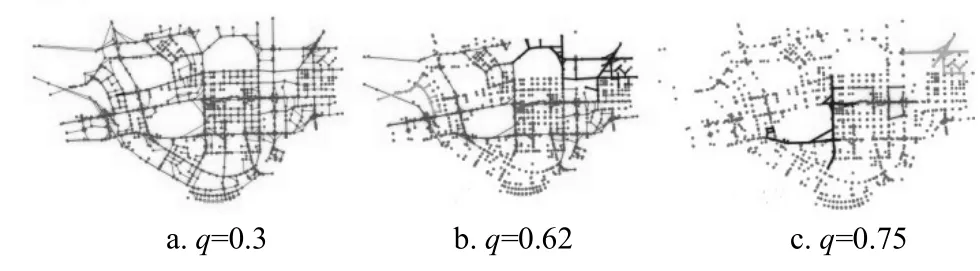
图8 福田区同一时段不同q值下的公交渗流网络

宝安区：分析结果如图9所示，与福田区类似的团簇分布结果类似，但在10：00-11：00时出现最大团簇时的q值大于福田区，说明宝安区的公交网络整体运行速度高于福田区。宝安区公交出行者若能接受10：00-11：00乘坐运行速度为日常最大速度45%的公交，则宝安区公交网络可基本连通。

图9 宝安区同一时段不同q值下的公交渗流网络

2) 同一q值不同时段下的公交网络运行速度演变。

选取 0.6q= 时福田区白天12小时(6：00-19：00)的公交网络进行分析，公交网络团簇分布如图10所示。

图10 0.6q= 时福田区公交网络运行演变

根据图10，6：00-7：00形成网络最大团簇，此时公交网络连通性最好，公交车可以将运行速度在绝大部分路段上维持在其最高速度的60%；7：00-8：00、13：00-14：00能形成一个较大的团簇，公交网络连通性较好，公交车的行驶速度在较大部分路段上可保持在其最高速度的60%；10：00-11：00为午间高峰，此时有较为明显的第二大团簇，公交网络连通性降低，不如早间及上午、下午时段；8：00-9：00为福田区的早高峰时段，公交网络连通性明显大幅度降低，能维持较高的公交运行速度 (最高速度的60%)的路段较少，行驶不够通畅；18：00-19：00为晚高峰时段，此时公交网络连通性最差，整个公交路网被分解成若干个小团簇，说明此时能维持较高公交运行速度的路段非常少，且局限在若干个独立的小区域(小团簇)，意味着受困于多个拥堵路段(速度低于最高速度的60%)。图10反映了该区域的整体交通状况的时间分布特性。

3 公交关键瓶颈路段识别

公交网络在发生渗流相变时，能发现一些连接不同团簇的关键路段，这些路段的速度值明显低于整个公交网络中其他路段的公交行驶速度值，同时临界阈值(cq)取决于该路段的速度值。定义这些关键路段为公交关键瓶颈路段。

由于实时公交网络各路段具有方向性，定义团簇中相连接的公交路段为“强联结段”。强联结段每对节点都可按照给定的路径方向互相可达。因此，在某个渗流公交网络中去掉某些路段，会导致联结不同团簇的有向路径的丢失并分解原强联结大团簇。

对深圳福田区晚高峰(18：00-19：00)在临界阈值附近(q值为0.52)时的公交渗流网络去掉1个路段，如图11a圆圈中，则原网络分解成两个团簇，如图11b所示；对深圳福田区晚高峰各个q值下的渗流公交网络逐一寻找强联结团簇，并当第二相强联结团簇达到最大时，即达到渗流阈值时，识别被去掉的公交路段。所有被去掉的路段，在临界阈值下连接不同的大团簇的路段即为关键瓶颈路段。而后，选择该关键瓶颈路段以及任意一条连接路段(非末端路段)及任意一条网络实际最拥堵路段(网络相对瞬时速度最低的路段)，增加3个被选路段的速度值，发现关键瓶颈路段本身的速度对整个公交网络的运行影响非常大，增加它的速度，可明显提高渗流阈值；而任意选取的公交路段和最拥堵路段，增加其路段上的公交运行速度，对整个公交网络的运行效率提升不大，如图11c所示。这也说明通过关键瓶颈路段与网络拓扑结构上常规意义上的瓶颈路段(最拥堵路段)并不一致，因为本文寻找的是整个公交网络的瓶颈，而非某一条公交线路或局部路段的瓶颈。

图11 公交网络瓶颈路段 (18：00-19：00，0.520.53q＜＜)

图12 公交网络瓶颈路段

静态网络瓶颈路段的识别通常是基于拓扑结构要素，确定网络连通性的关键路段。然而，公交网络是一个动态的系统，公交运行受到路段拥堵、乘客上下车、车辆进出停靠站等多种因素的干扰。因此，公交网络关键瓶颈路段应该同样是动态且变化的。如图11、图12所示，从一天中不同时段的关键瓶颈路段的识别中可看出，早高峰、午间、晚高峰期间的关键瓶颈路段完全不一样，这是由于一天中各时段的出行特征不同，导致公交出行需求不一，则整个公交网络的运行态势随时段变化。

4 结束语

本文选取深圳福田与宝安两个典型区域的一周的公交GPS数据进行处理分析，并基于渗流理论，呈现了真实公交网络的渗流过程。通过分析发现公交运行的允许速度值(即保证大部分公交路段的连通，形成大团簇)随时段、地区、工作日和非工作日的不同而呈现不同的特征。通过选取不同的临界阈值cq，识别公交网络中的关键瓶颈路段，对公交网络的运行效率优化有重要意义。运用本文提供的方法和思路，可观测城市公交网络运行的实时动态，迅速识别公交瓶颈路段并进行有效的控制与改善，比如在关键瓶颈路段设置公交优先措施(包括公交专用道、路口公交信号优先等)或者该路段实行机动车单行、公交车可双向行驶的管理措施或者实行若干工程措施(如拓宽道路、公交停靠站优化改造等)。这为提升公交网络运行效率提供了一个高效、低成本、低影响的方法。

[1]尹婷婷. 基于大数据的公交调度规则研究[D]. 北京： 北京交通大学, 2015.YIN Ting-ting. Research on bus scheduling rules based on big data[D]. Beijing： Beijing Jiaotong University, 2015.

[2]孙逢春, 王震坡, 王军. 北京市公共汽车平均车速统计分析[J]. 汽车工程, 2003(3)： 219-222, 242.SUN Feng-chun, WANG Zhen-po, WANG Jun. Statistical analysis on the average speed of public buses in Beijing[J].Automotive Engineering, 2003(3)： 219-222, 242.

[3]王明生, 黄琳, 闫小勇. 探索城市公交客流移动模式[J].电子科技大学学报, 2012, 41(1)： 2-7.WANG Ming-sheng, HUANG Lin, YAN Xiao-yong.Exploring the mobility patterns of public transport passengers[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(1)： 2-7.

[4]杨富社. 大城市常规公交动态调度理论与方法研究[D].西安： 长安大学, 2015.YANG Fu-she. Research on urban bus dynamic dispatching theories and methods[D]. Xi'an： Chang’an University, 2015.[5]HAGHANI A. Heuristic approaches for solving large-scale bus transit vehicle scheduling with route problem time constraints[J]. Transportation Research, Part A, 2002, 36(4)：309-333.

[6]PALMA A, LINDSEY R. Optimal timetable for public transportation[J]. Transportation Research Part B, 2001,35(8)： 789-813.

[7]金宁, 隽志才. 基于顾客满意度的城市公交服务水平[J].吉林大学学报(工学版), 2008, 38(S1)： 63-66.JIN Ning, JUAN Zhi-cai. Public transport service level based on customer satisfaction[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(S1)： 63-66.[8]LI Da-qing, FU Bo-wen, WANG Yun-peng. Percolation transition in dynamical traffic network with evolving critical bottlenecks[J]. PNAS, 2015, 20(1)： 669-672.

[9]BRODER A. Graph structure in the web[J]. Comput Netw,2000, 33(1-6)： 309-320.

[10]NEWMAN M E J, STROGATZ S H, WATTS D J.Random graphs with arbitrary degree distributions and their applications[J]. Phys Rev E, 2001, 64(2)： 026118.

[11]SOARES D J, ANDRADE J S, HERRMANN H J. Precise calculation of the threshold of various directed percolation models on a square lattice[J]. Physic A： Math Gen, 2005,38(21)： L413-L415.

[12]JENSEN I. Low-density series expansions for directed percolation： a new efficient algorithm with applications to the square lattice[J]. Physic A： Math Gen, 1999, 32(28)：5233-5249.

[13]ZHENG Y, LOU Y, ZHANG C, XIE X. Map-matching for low-sampling-rate GPS trajectories[C]//ACM Sigspatial International Conference on Advances in Geographic Information Systems. USA： ACM SIGSPATIAL GIS,2011： 211-219.

[14]KOLCHIN V F. Random graphs[M]. Cambridge：Cambridge University Press, 1999.

[15]NEWMAN M E J. The structure and function of complex networks[J]. Siam Review, 2003, 45(2)： 167-256.

[16]刘建军, 裴桂红, 薛强, 等. 城市交通网络的渗流力学模型[J]. 辽宁工程技术大学学报(自科版), 2007, 26(1)：63-65.LIU Jian-jun, PEI Gui-hong, XUE Qiang, et al.Mathematical model of traffic flow in city traffic network based on percolation theory[J]. Journal of Liaoning Technical University (Natural Science Edition), 2007,26(1)： 63-65.

[17]王璞, 黄智仁, 龚航. 大数据时代的交通工程[J]. 电子科技大学学报, 2013, 42 (6)： 806-816.WANG Pu, HUANG Zhi-ren, GONG Hang.Transportation engineering in the big data era[J]. Journal of University of Electronic Science and Technology of China,2013, 42(6)： 806-816.