阐述高中数学解题中代换法的灵活应用

◎李海峰

引言：学好数学，就要明白数学的解题过程，数学的解题过程就是把那些复杂未知的问题化成我们课本上的，能够用所学过的知识来解决的问题，从而来求解。那么，怎样转化它们呢？怎么去寻找它们之间的联系？这不仅需要我们平时勤学苦做题，达到对各种数学问题深刻理解其规律，还要掌握一定的方法，所以我们平时要注意总结归纳一些好的数学思想方法。下面，我们就数学中常用的代换法法做一些讨论，归纳其在方程、函数、不等式、数列等问题中的应用。

一、代换法求解方程

例：解方程组

解：设，原方程组化为：

这是一个二元一次方程组，易求得

由u＝10，得10，即.

经检验原方程组的解是

评析：看到分式方程组首先我们想到化为整式方程组，通过巧妙换元我们把分式方程组化成一个一元二次方程组就很容易求解了

二、运用代换法法研究函数问题

例：定义在 R上的函数 y＝f（x），当 x＞0时，f（x）＞1，且对任意 a、b∈R有 f（a+b）＝f（a）·f（b），又 f（0）≠0。

（1）求证：f（0）＝1；

（2）求证：对有 x∈R，有 f（x）＞0；

（3）求证：f（x）是 R上增函数；

（4）求证：解不等式：f（x）·f（2x-x2）＞1证明（1）由得因为所以 f（a+b）＝f（a）·f（b）得 f（0+0）＝f（0）·f（0）。因为 f（0）≠0，所以 f（0）＝1。

（2）当 x≥0时，f（x）≥1＞0；当 x＜0时，因为 -x＞0，所以 f（-x）＞0。由 f［x+（-x）］＝f（x）·f（-x），知 f（x）＝f（0）f（-x）＞0。综上知：x∈R，有 f（x）＞0。

（3）设 x1＜x2，则 x2-x1＞0，因为 f（x2）＝f（x2-x1+x1）＝f（x2-x1）·f（x1）；又当x2-x1＞0时，f（x2-x1）＞1，且f（x1）＞0。所以f（x2）＝f（x2-x1）·f（x1）＞f（x1），因此 f（x）是 R上增函数。

（4）由 f（x）·f（2x-x2）＞1，又 f（0）＝1，故 f（x+2x-x2）＞f（0），又f（x）是 R上增函数，所以3x-x2＞0，所以0＜x＜3。

评析：对于未知函数，要研究它与坐标轴的关系、单调性，我们可以进行常值代换，通-x与x相加等于0，这个特殊值，来进行-x与x之间的变换寻找解题思路。

三、运用代换法求解不等式

例1.若：1≤x2+y2≤2，求证≤x2-xy+≤3

解：由1≤x2+y2≤2，设x＝rcosθ，y＝rsinθ（1≤r≤0≤ θ≤2π）所以x2-xy+y2＝r2-r2sinθ＝由≤1-

评析：题设条件表示圆环，联想到圆的参数方程，进行三角代换，通过三角函数性质解决问题。

例2.已知 a、b、c≥0，求证：

证：由可联系到复数的模。

设：z1＝a+bi，z2＝b+ci，z3＝c+ai（a、b、c＞0），则左边 ＝｜z1｜+｜z2｜+｜z3｜≥｜z1+z2+z3｜＝｜a+b+c+i（a+b+c）｜＝（a+b+c）

评析：通过复数代换，使复杂难懂的式子化成我们学过的复数模运算，以及三角形三边关系。

四、求解各种极值、最值

例1.设 x，y，z＞0，x+y+z＝1，求的最小值。

解：

评析：通过等量代换把x+y+z＝1代入式子，再利用均值不等式求证.

例2.求函数的最小值。

解：令则代入

得

当 t＝0，即时，f（x）取最小值

评析：引入变量，把无理函数化为二次函数在特定区间上的求值问题，化未知为已知。

五、一些求字母取值范围的求解问题

例：设ax2-4ax+1＝0方程的两根为α、β满足不等式｜logα-logβ｜≤1，试求实数α的取值范围。

解：由 α+β＝4，可设α＝2+p，β＝2-p（0≤p＜2）注意到，此时可用p的表达式表示α，再根据p的范围确定α的范围。

∵ α＝2+p，β＝2-p（0≤p＜2）

∴ ｜logα-logβ｜≤1，有，解得即0≤p

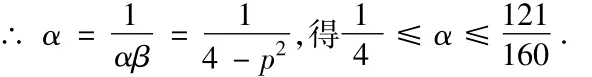
评析：通过设变量联系题设已知与所求问题.

结束语：通过代换法我们化未知为已知，化生疏为熟悉，中学阶段我们有很大一部分题，可以通过代换法简化运算来求解。在高等数学中，我们也经常要用代换法来求函数的极限、积分、求解微分方程，所以要学好数学，必须学会并熟练运用代换法方法，通过上面涉及的方程、函数、数列、不等式等几个方面的应用代换法方法解题，帮助学生更深层次地了解代换法的实质，学会运用代换法方法，去联系问题与所给条件之间的关系，运用所学知识解决问题。

［1］陈卫卫.分析在高中数学解题中代换法的灵活运用［J］.高中数理化，2016（22）：8-8.

［2］徐霜.浅谈代换法在高中数学解题中的灵活应用［J］.数理化解题研究，2017（25）：21-22.

［3］方胜娟.代换法在高中数学解题中的应用［J］.数理化解题研究，2015（15）：13-13.

［4］陈果.代换法在解高中数学题中的应用［J］.语数外学习（高中版中旬），2016（9）.

［5］谭宇.代换法在解高中数学题中的应用［J］.语数外学习（高中版下旬），2017（1）.