寻根，探求数学教学的本源

江苏省徐州市铜山区三堡实验小学 刘艳红

问题：在教学转化策略练习时，学生的一道练习题引起同年级教师的讨论。

求下面图形的周长。

“直接告诉学生三个小半圆弧的周长和大圆弧的周长相等就行。”

“这样不行，必须让学生明白为什么三个小半圆弧的周长和大圆弧的周长相等。让学生知其然知其所以然。”

“举例，三个小圆的直径分别看作一个数字，比如，分别是2厘米、1.5厘米和0.5厘米。学生经过计算发现三个小半圆弧的周长和大圆弧的周长相等。这个图形的周长就是大圆弧所在圆的周长。”

……

教师们提出自己的见解。举数字，从特殊到一般，不完全归纳。不失是一种不错的见解。

我于是采取了举数字的方式，列了一黑板的算式。先算出三个小半圆弧的周长，再算出大半圆弧的周长，让学生进一步发现小圆弧的周长等于大圆弧的周长，从而得到这个图形的周长就是大圆弧所在圆的周长。

总是感觉自己讲得是相当的透彻，学生应该都会了。事与愿违，可学生就是不领情。进入总复习了，这个题目又来了，班里百分之八十的孩子不知如何入手。

思考：方法讲了，孩子当时知其然也

得出结论：它们的周长和上面两个图形的周长相等。

变式3：（课件演变）把两个小半圆弧由直径2厘米分别变成直径3厘米和直径1厘米的半圆弧，图形的周长有变化吗？知其所以然了，为什么孩子记不住，现在照错不误呢？我陷入了沉思。

我们教师在教授知识时，为了培养孩子数学思维，非常注重让学生自主发现问题，用探究的方式解决问题。这没有错，但是我们往往忽视让学生在数学学习过程中体验数学本源所在。“万物有本，万水有源”，任何事物的产生都会有其根源所在。在教学中找准切入点，寻求知识的产生、演变过程，要遵从学生认知发展规律。教师在学生认知初期，应有意识地把握教学内容之间的联系，注意从不同角度，采取不同形式挖掘知识的内涵和外延，并将其融入自身的认知体系中；不断拓展学生的思维宽度和广度，培养数学素养。

寻根求源：（在今年教学圆的周长练习时，我这样教学的。）

引子：分别计算直径4厘米和一个直径2厘米的圆的周长。

学生计算后让学生说说自己的发现。学生会发现直径4厘米的圆周长是直径2厘米圆周长的2倍，反之，直径2厘米的圆周长是直径4厘米圆周长的一半。

变式1：（课件出示）

得出结论：直径4厘米半圆弧的长度和直径2厘米的圆的周长相等。

变式2：（课件演变）把直径2厘米的圆进行分割，与直径4厘米的半圆弧组合成如下图形：

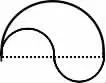
这个图形的周长怎样计算？

得出结论：这个图形的周长是直径4厘米半圆弧和直径2厘米的圆弧的长度之和。学生很容易推算出这个图形的周长其实就是求直径4厘米圆的周长。

继续演变，衍生出下面两个图形。

得出结论：学生经过讨论，发现两个小半圆弧的直径之和是4厘米，无论两个小半圆弧的直径多少，只要它们的直径之和是4厘米，图形的周长都是大半圆弧所在圆的周长。

在小学阶段，学生的思维正处在由直观思维向抽象逻辑思维过渡的阶段。由于学生受思维限制，对于知识理解片面。尽管是自己接触过的理解，如果没有实践训练过，就会无从下手。如果一开始就把问题抛给学生，学生一定蒙圈。这时教师再举例例证，学生只会当时知道这样一个结论。事情过后，他们就会抛之脑后。因为孩子没有亲自参与知识探究，根本没融入自己的认知体系当中来，不符合学生认知发展规律。

我们教师应善于应用变式指导数学教学，举一反三把由一种情况衍生出来的各种变化呈现给学生，帮助学生形成完整的知识结构。

以上一系类的变式训练由易到难，环环相扣，顺应学生认知发展的规律，既巩固了学生所学习的数学知识，又培养了学生的发散性数学思维。从不同角度不同形式进行变形，而本质属性不变。在变中使学生感受到数学的美妙，变中看到不变，体会数学知识“万变不离其宗”的道理。本题中图形蕴含着转化的策略，转化就是对图形方向，形状，位置进行不断地变形 ，让学生学会数学思想和思考方法。

在课堂教学中教师应有追溯数学知识本源的精神，深入学习数学，让数学知识更加明晰，有效提高教学实效性，提高学生的数学素养。