典型 趣味 开发 共享

【关键词】综合与实践活动;课例分析;教学策略

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2018）35-0019-03

《义务教育数学课程标准（2011年版）》颁布以来，各地对初中数学“综合与实践”活动做了大量、有效的研究，配套的教材、课堂教学活动，以及各地中考试题的渗透等，都对这项內容的研究做了很好的助推。

目前，部分地区、学校在“综合与实践”活动实施过程中，或以方法教学代替“综合与实践”活动过程的辅导，陷入仅传授知识的误区;或等同于其他常规内容开展教学，使学生缺乏深度体验。据此，笔者拟就一节“综合与实践”活动课的教学设计与课堂开展情况，从教学策略角度谈谈初中数学“综合与实践”活动应该凸显的关键点及思考。

一、选择典型主题

初中数学“综合与实践”活动的主要目的是培养学生运用有关知识与方法解决实际问题，培养学生的问题意识、应用意识和创新意识，积累学生的活动经验，提高学生解决现实问题的能力。

在选择活动主题时应关注与实际生活联系的问题，关注便于学生理解的问题，关注数学内部多个知识综合的问题等，以提高研究的针对性与实效性。

为考查学生综合运用三角形、四边形和圆的相关知识解决实际问题的能力，笔者选用了如下与实际生活相联系的问题开展探究活动。

问题：某地有四个村庄E、F、G、H（其位置如图1所示），现拟建一个电视信号中转站，为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（距离越小，所需功率越小），此中转站应建在何处？请说明理由。

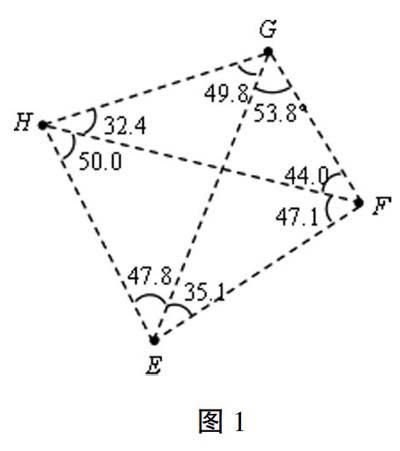
（说明：这个问题具有一定的现实意义，与之类似的问题还有雷达、Wi-Fi的选址等等。学生拿到问题之后也有一定的积极性，并着手开始研究。）

实际上，我们在平时的教学中，可以放手让学生寻找问题，从而激发学生观察生活、发现与探究问题的兴趣，确定“综合与实践”活动的研究主题。如：学习了全等三角形、相似三角形、锐角三角函数等知识后，就可以引导学生寻找可以运用上述知识解决的实际问题，如测量建筑物的高度、测量河宽等;学习了平移、旋转、翻折（轴对称）等知识后，可以引导学生寻找生活中一些精美图案与上述知识之间的关系，自主设计一些与此相关的图案等等。

选择“综合与实践”活动的研究主题时，应注意以下细节：第一，以任务驱动方式指导学生学习观察、考察、调查、访问等实践活动的方法，发现、提出问题;第二，指导学生运用文字、图形、摄影、录像等多种手段记录发现问题的素材;第三，指导学生对所发现问题进行背景分析，猜想解决问题需要的数学知识、方法等。

总之，选择综合与实践活动研究的主题应具有典型性、实用性、有效性、综合性，与学生所学知识、方法要紧密联系，避免选择大而空的问题。

二、创设趣味情境

对有一定难度问题的探究，学生常常会有畏难情绪，这与他们的心理特征、年龄特征有关。托尔斯泰说过：“成功的教学所需的不是强制，而是激发学生学习的兴趣。”

因此，在选定研究主题之后，教师在创设问题情境中应注意教学策略的安排，可选择与研究主题相关的有趣情境，选择适合学生开展活动的研究方式，选择便于学生动手操作、有益于加深理解的活动形式等。

提出“中转站问题”一周之内，学生基本没有头绪，只是意识到该问题会与三角形、四边形、圆等知识相关，但无法解决问题。为此，笔者创设了一些有益于学生深入理解问题的情境，既激发学生的探究兴趣，又帮助学生初步理解“覆盖圆”的含义。具体如下：

展示生活中的覆盖现象（出示图片）：张家界市生态优良，属中亚热带山原型季风湿润气候，四季分明。全市森林覆盖率达66.98%，核心景区为98%。

通过这些学生熟知的生活现象，让学生基本了解生活中的覆盖问题，为激发学生进一步探究“中转站问题”奠定了重要基础。

初中数学“综合与实践”活动的主旨是将生活中的数学与课堂中的数学有机结合，实现人人学有价值的数学，培养学生“用数学”的意识。将选定的“综合与实践”活动内容落实在课堂教学时，可采用如下策略：安排学生分组汇报前期的研究情况，包括展示相关图片、录像等素材;教师演示事先准备好的相关问题情境，以利于激发学生探究兴趣，帮助学生准确理解研究主题。

三、开发合作内容

在开展“综合与实践”活动的过程中，选定研究主题是前提，挖掘、开发实际生活问题情境是铺垫，而开发具体的研究内容、研究方法则显得尤为关键。

开发合作内容的教学策略应遵循以下原则：有合作的必要，不流于形式;有合作的价值，不浮于表面;通过合作，有利于学生思维水平的提高;通过合作，有利于激发学生进一步探究的欲望等。

笔者在设计“中转站问题”的探究内容与方法时，安排了如下一些操作与探究活动。

1.操作：（1）已知线段AB=4cm。分别用半径为1cm、2cm、3cm的圆覆盖线段AB，你发现了什么？（2）已知等边三角形ABC的边长为4cm。分别用半径为2cm、3cm的圆覆盖△ABC，你发现了什么？

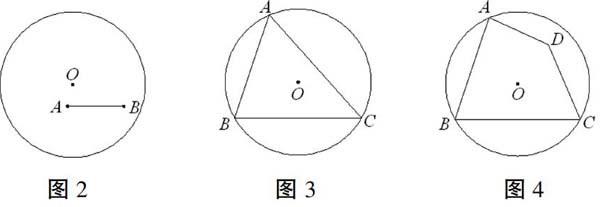
2.概念：对于平面图形A，如果存在一个⊙O，使图形A上任意一点到圆心O的距离都不大于⊙O的半径r，则称图形A被⊙O覆盖。⊙O称为图形A的覆盖圆，其中半径最小的⊙O称为图形A的最小覆盖圆。例如：图2中的线段AB被⊙O覆盖，图3中的△ABC被⊙O覆盖，图4中的四边形ABCD被⊙O覆盖。

3.探究活动1：

如图5，已知线段AB。

（1）请画出线段AB的一个覆盖圆;（2）线段AB存在最小覆盖圆吗？如果存在，请画出来。

4.探究活动2：

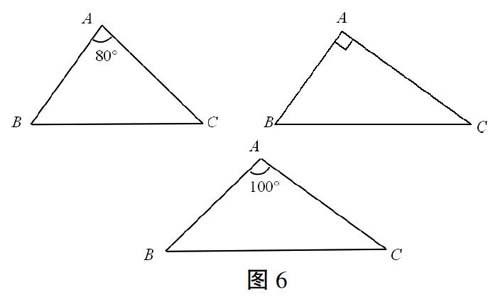
如图6，3个三角形分别是锐角三角形、直角三角形和钝角三角形。（1）请分别作出它们的最小覆盖圆;（要求用尺规作图，保留作图痕迹）（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论。

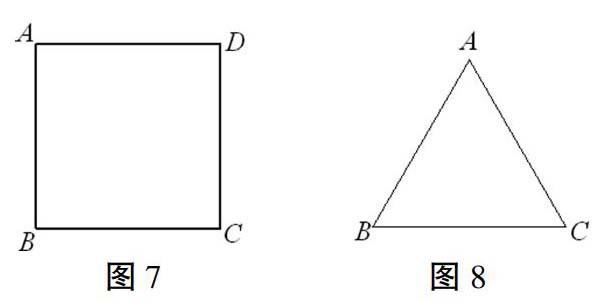
5.探究活动3：（1）如图7，正方形ABCD的边长为1cm，则它的最小覆盖圆半径是 _____ cm;（2）如图8，等边三角形ABC的边长为1cm，则它的最小覆盖圆半径是_____ cm。

6.探究活动4：解决上述“中转站”问题。

（说明：本环节共安排了1个操作活动与4个探究活动。）

操作活动关注了知识发生的过程，学生通过分组操作、交流后都有一定的发现，为后面引出新概念提供保证;也为学生进行其他探究提供了思维的方式、方法。

第1、2两个探究活动体现由易到难的设计原则，关注学生的探究方式、探究习惯和探究能力。探究活动3主要是将学生亲身体验、探究获得的结论进行简单的应用。但这里的设计不是简单的重复，而是有创造性的运用。探究活动4的难度明显提高了，也突出了数学的实用性。要求学生根据探究过程中积累的活动经验、形成的分析解决问题的方法，来解决实际问题。

据此可以看出，设计与开发具体的探究内容时应注意以下几点：第一，关注学生的基础，选择适合学生层次的问题梯度;第二，设计的问题易操作，兼顾学生的独立思考与合作学习;第三，设计的问题有一定的思维含量，要难易适中，把握好这一点极为重要。

四、实现共享成果

从选定初中数学“综合与实践”活动探究的主题开始，到确定探究方案、探究方法，从而完成主题的探究过程。那么，学生的活动成果该以什么方式来呈现、表达？

就呈现方式的策略而言，笔者认为，成果应利于共享，利于交流，可采用数学小报、班级板报、数学小论文等形式呈现，定期积累归入学生数学成长学习袋中，便于收集。就表达形式的策略而言，可让学生学习陈述、学习交流分享、学习反思等方式开展。

综上，在实施初中数学“综合与实践”活动时，要优化教学策略，在主题选择、情境设置、合作探究及成果共享等方面，都应得到应有的重视，真正推动数学“综合与实践”活动在初中阶段的有效实施。

【参考文献】

[1]欧阳新龙，肖川.《义务教育數学课程标准（2011年版）》解读[M].武汉：湖北教育出版社，2012.

[2]杨裕前，董林伟.数学综合与实践活动[M].南京：江苏科学技术出版社，2008.

[3]王四宝.一节“实践与综合应用”课的教学片断与思考[J].中学数学教学参考，2009（04）.