旋转弹舵机控制滞后及延迟补偿时间分析

连 捷, 姚晓先, 郭致远

(北京理工大学宇航学院, 北京 100081)

0 引 言

弹体滚转可改善导弹飞行的稳定性,增强系统对推力偏心和安装误差的鲁棒性[1]。应用双通道十字鸭舵布局控制具有更好的稳定性和控制效率[2-4]。旋转弹由于弹体绕纵轴旋转,因此其俯仰和偏航通道存在一定的耦合[5-6]。为消除耦合,需要进行解耦和对舵机进行补偿[7-11]。陈罗婧等计算舵机延迟对控制系统的影响,利用前馈补偿方法进行解耦[12],但此方法需要获取飞行速度、转速和高度等相关信息,难以实现工程应用;毕艳超等分析准弹体坐标系下舵机延迟特性,分析滞后角与对应相角之间的关系[13],但未提出补偿方案;于剑桥采用弹体滤波,由法向加速度延迟确定舵机延迟补偿时间[14],但只是从舵机自身角度出发,只考虑了舵机指令响应补偿,未考虑输入指令信号存在滞后的情况。因此,为了解决舵机控制滞后问题,实现更好的控制效果,需从整体角度出发,对舵机输入指令信号和指令响应信号两方面都进行分析。

本文以双通道旋转弹上的十字布局鸭舵为例,定义理想周期平均控制力和实际周期平均控制力的夹角为滞后角,建立控制模型,理论推导滞后角的计算公式。结合工程实际,从系统组成的角度出发分析指令的形成与传输过程和滞后存在的原因;提出舵机控制力延迟补偿时间的计算方法和滞后角补偿算法,对补偿结果进行了实验验证,为分析舵机控制滞后提供了研究方法和依据。

1 控制模型建立

坐标系oxyz和ox1y1z1分别为弹体坐标系和准弹体坐标系[15]。旋转弹采用十字布局鸭舵, 由两对相互垂直的舵面(1#、3#和2#、4#)和两路舵机构成,每个舵机控制一对舵面,每对舵面的舵机偏转角相同。旋转弹每旋转半周舵机指令换向一次。舵面布局如图1所示。

在弹体坐标oxyz下,1#和3#舵机固定在z轴上,舵机偏转角为δy,指向oy轴正向为正。2#和4#舵机固定在y轴上,舵机偏转角为δz,指向oz轴正向为正。它们形成的控制力分别为Fcy、Fcz。当舵偏角为正时,产生的控制力为正;反之,产生的控制力为负[16]。其中

(1)

在准弹体坐标ox1y1z1下,Fy1为舵机控制力在竖直方向上的分量,Fz1为舵机控制力在水平方向的分量。假设弹体坐标系相对于准弹体坐标系旋转γ=ωt(ω为旋转频率)角度,如图2所示。

图2 坐标系Fig.2 Coordinate system

根据几何关系对舵机偏转角δy、δz进行分解,可得到δy、δz在oy1轴和oz1轴上的分量,即俯仰方向和偏航方向的等效舵偏角δy1、δz1[17]。

δy1=δycosγ-δzsinγ

(2)

δz1=δysinγ+δzcosγ

(3)

即

(4)

变形,可得

(5)

同时,将弹体坐标系中的控制力转换到准弹体坐标系中,得到

(6)

将式(1)和式(5)代入式(6),得到竖直方向和水平方向的控制力与等效舵偏角的关系:

(7)

由于弹体具有低通滤波性,故只有舵机控制力的周期平均值才能得到弹体的响应。对舵机形成的控制力随弹体滚转一周在竖直和水平方向的分量进行积分,可得

(8)

式中,F1y为oy1轴方向的周期平均控制力;F1z为oz1轴方向的周期平均控制力。

所以作用于旋转弹上的周期平均控制力为

F=F1y+F1z

(9)

舵机的实际偏转角可通过舵机输出信号得到,通过式(4)可计算出实际等效舵偏角。将实际等效舵偏角和理想等效舵偏角分别用向量δ和向量u表示。通过上述分析,可得到实际周期平均控制力Fδ和理想周期平均控制力Fu,定义Fδ和Fu的夹角为滞后角,用φ表示,如图3所示。

δ=(δy1,δz1)

(10)

u=(uy1,uz1)

(11)

Fδ=(F1y,F1z)

(12)

Fu=(Fy,Fz)

(13)

(14)

式中,uy1、uz1分别为俯仰和偏航方向的理想等效舵偏角;Fy、Fz分别为竖直和水平方向的理想周期平均控制力。

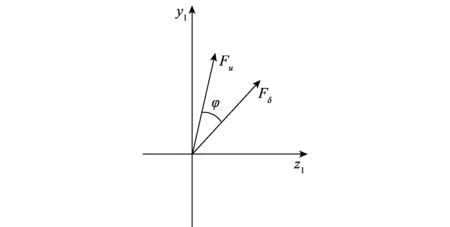
图3 实际周期平均控制力和理想周期平均控制力Fig.3 Real average control force and theoretical average control force

利用式(7)、式(8)对式(14)化简,得

(15)

由式(15)可以看出,滞后角可以利用实际等效舵偏角和理想等效舵偏角比较而求得。而实际等效舵偏角可通过实验测量结果求出[18-19]。

2 滞后原因分析

所研究的旋转弹控制系统主要由地磁陀螺、弹载计算机、舵机系统、测高系统等组成。弹载计算机根据飞行状态给出所需要的等效指令舵偏角,然后根据地磁陀螺测量的滚转角数据和式(5)计算出舵机输入指令,将其输入舵机动力学方程,得到实际的舵机指令响应值,再将该响应值输入弹体动力学。整个指令形成与传输过程如图4所示。

图4 舵偏指令形成与传输过程Fig.4 Formation and transmission of the command

从上述分析可以看出,造成舵机控制力存在滞后的原因主要有两方面:一是舵机输入指令信号存在延迟;二是舵机偏转角指令响应值(舵机实际偏转角)存在延迟。

2.1 舵机输入指令信号延迟分析

舵机输入指令信号是根据地磁陀螺测量的滚转角和弹载计算机的处理结果形成的。因此地磁陀螺测量和弹载计算机处理过程的延迟会导致舵机输入指令信号存在延迟[20-21]。

2.1.1 地磁陀螺滞后原因

地磁陀螺用于测量旋转弹的滚转角。测量原理是通过测量地磁场来计算出旋转弹的滚转角[22-25]。地磁陀螺在数据生成和传输过程中会存在延迟,因此会形成滞后。

图5为地磁陀螺生成数据的时序,传感器采样到计算形成滚转角数据需要t1ms,传送数据时间t2ms,因此地磁陀螺数据产生的延迟时间τ1=t1+t2。在这段延迟时间过程中,弹体已经旋转了一定的角度,故地磁陀螺数据传输延迟将导致舵机实际控制滞后于理想控制。

图5 地磁陀螺生成数据时序Fig.5 Time sequence of geomagnetic gyro

在实际应用中,地磁陀螺测量的滚转角数据在一个周期内不是严格线性变化的,与理想测量值存在误差,这样的误差会导致滞后的产生;在地磁陀螺装订正确的前提下,其测量的滚转角的零点与绝对零点之间存在差值,这样的零点误差也是滞后产生的原因之一。在相同转速下,地磁陀螺测量的滚转角与实际滚转角的对比结果如图6所示。同时计算两者之间的差值,如图7所示。

图6 地磁陀螺测量值与实际滚转角对比Fig.6 Comparison between the angle of geomagnetic gyro and the actual rolling angle

图7 实际滚转角与地磁陀螺测量值的差值Fig.7 Difference between actual rolling angle and calculation angle of geomagnetic gyro

从图6和图7中可以看出,由于上述原因,地测陀螺测量的滚转角存在滞后。

2.1.2 弹载计算机滞后

在飞行过程中,弹载计算机根据飞行状态和滚转角信息计算出舵机输入指令信号,并将其传输给舵机。弹载计算机生成舵机输入指令的时序与地磁陀螺类似,形成舵机输入指令的周期为t3ms,向舵机发送数据时间为t4ms。因此弹载计算机的延迟时间τ2=t3+t4。

2.2 舵机指令响应信号延迟分析

响应性能良好的舵机系统数学模型可以等效为一阶惯性环节。随着转速的增大,伺服机构的跟踪误差会增大。舵机响应慢是产生指令响应滞后的主要原因[26]。

舵机特性可表示为

(16)

即输入指令为uδ=Asin(ωt)时,舵机输出为δ=Asin(ωt+φ(ω,A)),φ(ω,A)为舵机输入信号频率为ω,幅值为A时的相角滞后。

准弹体坐标系下舵机偏转角信号频率较低时,准弹体坐标下舵机偏转角的控制延迟近似舵机在弹体旋转频率处的相角滞后。因此可认为φ(ω,A)为舵机实际偏转角相对于输入指令的滞后值。利用正弦波扫频法可获得舵机的幅频和相频特性曲线,从而求出在不同指令幅值和旋转频率下的舵机指令响应滞后角φ1(ω,A)。

综上所述,旋转弹控制力滞后角φ是由于舵机输入指令滞后和舵机指令响应滞后形成的,其计算公式如下:

φ=φ1+φ2

(17)

式中,φ1为输入指令信号滞后角度;φ2为指令响应滞后角度。

3 确定延迟补偿时间与滞后补偿方法

研究对象采用固定斜置角度的尾翼,使得弹体转速保持在5 r/s至15 r/s之间。假设旋转频率ωx=8 Hz,uy1、uz1满足

(18)

3.1 舵机输入指令信号延迟时间计算

在实验过程中,使用与地磁陀螺测量原理不同的角度传感器(变压器原理)测量滚转角,此角度传感器具有响应快、精度高、抗干扰能力强等特点,认为其测量结果无延迟。因此将角度传感器测量的滚转角作为理想滚转角,地磁陀螺的结果为测量的滚转角。角度传感器与地磁陀螺测量结果如图8所示。

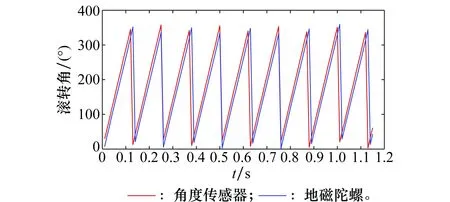
图8 滚转角测量结果Fig.8 Measuring results of rolling angle

从图8中可以看出,地磁陀螺测量结果相对角度传感器存在一定的滞后值。在考虑指令信号延迟和舵机指令响应滞后已补偿(即令输入指令超前φ1)的情况下,舵机特性可表示为

(19)

式中,φ(ω)为输入信号频率为ω、幅值为A时输入指令信号的相位滞后角。得到相应的舵机输入指令信号为

(20)

将输入指令信号输入舵机模型式(19),计算求得舵机输出式为式(21),并采集舵机输出信号,如图9所示。

(21)

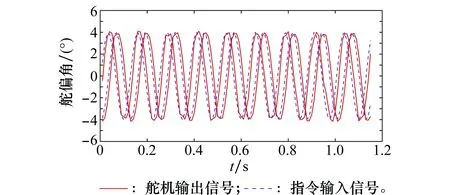
图9 舵机输入与输出信号Fig.9 Input single and output single of actuator

进而求得等效舵偏角为式(22),指令信号滞后角为式(23)。根据采集得到的实际舵机偏转角输出信号计算出的实际等效舵偏角如图10所示。

(22)

φ2=φ(ω)

(23)

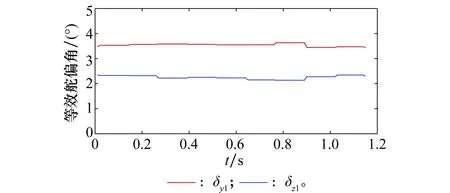
图10 等效舵偏角Fig.10 Equivalent deflection angle of actuator

弹体动力学是一个低通滤波器,可构造弹体滤波器对δy、δz进行滤波。导弹动力学传递函数为

(24)

所采用的滤波器形式为

(25)

根据滤波后的δy、δz,求得实际指令滞后角,并对其进一步处理,利用式(26)得到指令延迟补偿时间。计算结果如图11、图12所示。

φ=0.36ωτ

(26)

式中,ω为旋转频率;τ为延迟补偿时间。

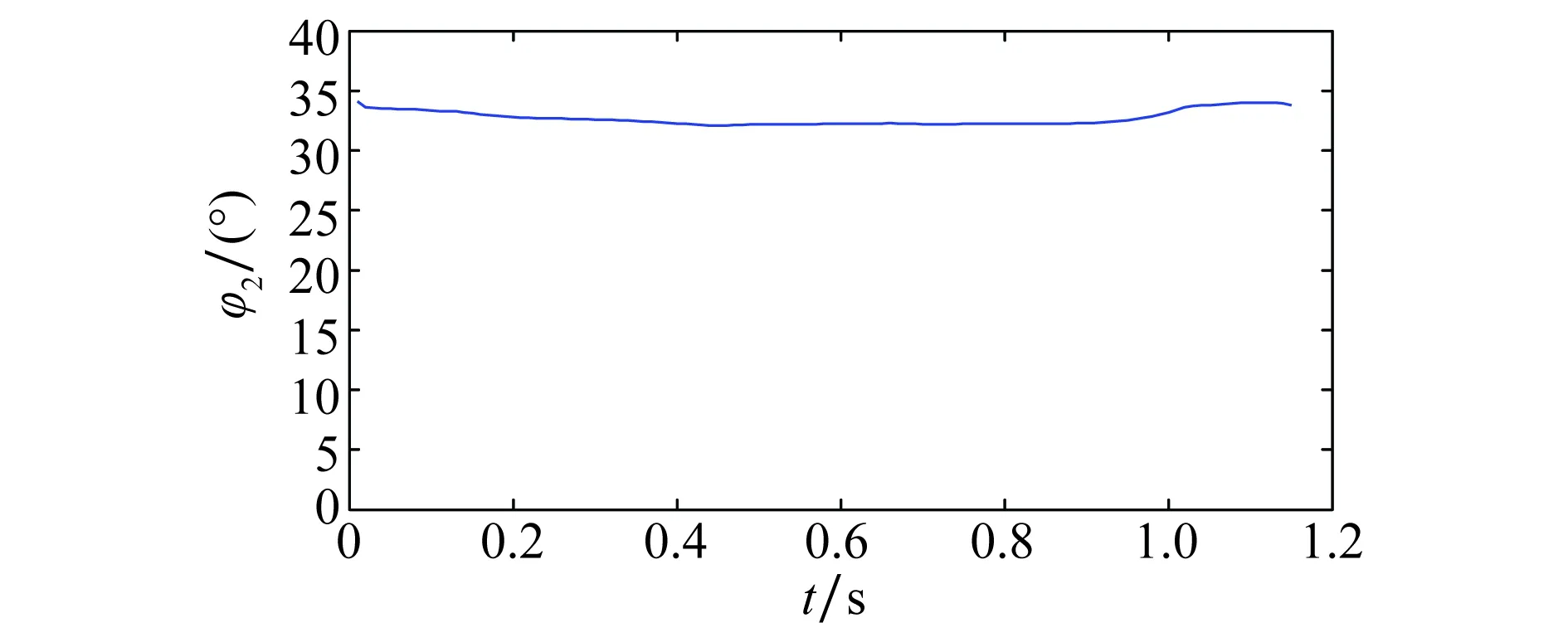
图11 指令滞后角Fig.11 Lag angle of command

图12 指令延迟补偿时间Fig.12 Delay compensation time of command

对数据进行处理,得到输入指令滞后角φ2的均值为32.7°,方差为0.37°。补偿时间的均值为11.4 ms,方差为0.05 ms。

改变指令指频率(弹体转速)和指令幅值进行测试,得到不同指令幅值、不同旋转频率下的指令滞后角如图13所示。

图13 不同指令、旋转频率下滞后角度Fig.13 Lag angle of different command and frequency

利用式(26)和最小二乘法对指令滞后角数据进行处理,求得幅值为4°时的补偿时间为11.6 ms,幅值为6°时的补偿时间为11.1 ms,与幅值为4°、旋转频率为8 Hz时求得的补偿时间11.4 ms基本接近,因此可将11.4 ms作为所研究指令幅值、频率下的输入指令信号的延迟补偿时间。所需补偿的滞后角φ2=0.36×11.4×ω。

3.2 舵机指令响应延迟时间

利用正弦扫频法,得舵机的幅频和相频特性曲线如图14所示[27],从而求出在不同指令幅值和旋转频率下的滞后角φ1(ω,A)。从扫频结果中可以得出,A=4,ω=8时,舵机指令响应滞后值φ1=11.1°。

图14 舵机幅频特性和相频特性曲线Fig.14 Amplitude-frequency and phase-frequency characteristics of actuator

由于弹体转速不超过15 r/s,从图14中可知舵机相角在此范围内具有良好的线性度,利用式(19)和最小二乘法可得,舵机延迟补偿时间约为3.8 ms。

因此,根据上述分析可知,当弹体旋转频率较低时,舵机周期平均控制力所需延迟补偿时间包括两部分,形成舵机输入指令信号的延迟时间11.4 ms和舵机指令响应延迟时间3.8 ms,总延迟补偿时间为3.8+11.4=15.2 ms,舵机周期平均控制力滞后角为

φ=0.36×15.2×ω

(27)

3.3 滞后补偿方法

对于所研究的旋转弹,由于弹体转速相对较低,因此舵机周期平均控制力延迟补偿时间相对稳定,此时其滞后角随着弹体旋转频率的变化而变化。如果给输入指令一个相位超前量,这样能抵消舵机滞后的影响。根据分析结果,提出滞后补偿方法:弹载计算机控制程序利用式(27),根据延迟补偿时间和当前转速实时计算滞后角(即所需的指令超前量),同时令控制指令超前所需补偿的角度,从而形成准确的控制力。此超前角度包括两部分:舵机输入指令信号滞后角和舵机指令响应滞后角度。

采用上述方法对舵机进行补偿,得到补偿后滞后角计算结果如图15所示。

图15 补偿后滞后角度Fig.15 Lag angle after compensation

从图15中可以看出,经过补偿后,滞后角在-1.8°和1.1°之间波动。若模拟实际滚转角,并根据上述分析内容,得到实际滚转角下不同指令、不同频率下的指令滞后角如图16所示。

图16 实际滚转角下不同指令、旋转频率下滞后角度Fig.16 Lag angle of different command and frequency with actual roll angle

将图16所求的滞后角和舵机对应指令幅值和旋转频率下的滞后角相加,并利用式(27)进行补偿,并将得到的补偿结果与图15的计算结果进行对比,对比结果如图17所示。

图17 滞后角对比结果Fig.17 Comparison of lag angle

从图17中可以看出,两种情况下补偿后的滞后角相差较小,均在可接受的范围内。实验结果表明,此方法具有较好的补偿效果。

当弹体旋转频率不断增大时,由于舵机特性趋向于非线性,因此对指令响应补偿时间的影响明显增大,滞后角度需实验测量,此时可对不同的转速补偿所对应的滞后角度值。

4 结 论

本文从舵机控制力角度出发,建立控制模型,推导得出控制力滞后角可用等效舵偏角进行计算;分析得到滞后形成的原因主要是:地磁陀螺和弹载计算机导致的输入舵机指令信号滞后和舵机性能导致的舵机指令响应信号滞后两方面;对舵机输入指令信号和指令响应信号延迟补偿时间的计算结果表明,在弹体转速较低的情况下,延迟补偿时间为常数;根据分析结果,提出滞后补偿的方法,即利用延迟补偿时间,根据弹体转速求出所需补偿角,令指令超前此补偿角。本文研究结果已经半实物仿真和飞行试验验证,具有良好的补偿效果。

参考文献：

[1] 范世鹏,吴广,孙友,等.滚转导弹控制耦合特性分析与解耦方法[J].系统工程与电子技术,2017,39(2): 398-403.

FAN S P, WU G, SUN Y, et al. Analysis of control coupling characteristic and forward decoupling technique for rolling missile[J].Systems Engineering and Electronics,2017,39(2):398-403.

[2] PHILIPPE W, SPILIOS T, YANNICK M.Flight dynamics properties of 155 mm spin-stabilized projectiles analyzed in different body frames[C]∥Proc.of the Atmospheric Flight Mechanics Conference, 2010: AIAA-2010-7640.

[3] LI K Y, YANG S X, ZHAO L Y. Stability of spinning missiles with an acceleration autopilot[J]. Journal of Guidance, Control and Dynamics, 2011, 34(1): 278-283.

[4] YAN X Y, YANG S X, XIONG F F. Stability limits of spinning missile with attitude autopilot[J]. Journal of Guidance, Control and Dynamics, 2012, 35(3):774-786.

[5] 宋韬,林德福,魏志军,等.滚转导弹过载驾驶仪控制耦合解耦算法研究[J].兵工学报, 2014,35(4):454-460.

SONG T,LIN D F,WEI Z J, et al. Research on decoupling algorithm for control coupling of a spinning missile autopilot[J]. Acta Armamentarii, 2014, 34(4): 454-460.

[6] Richard L. Analysis of control and guidance of rolling missile with a single plane of control fins[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2010: AIAA-2000-37028.

[7] ZHANG W, XIA L Y, FU H C. Analytical decoupling control of a generic hypersonic vehicle based on internal model control[C]∥Proc.of the IEEE 36th Chinese Control Conference,2017:6163-6168.

[8] DUAN Z S, HUANG L, YANG J Y, et al. On decoupled or coupled control of bank-to-turn missiles[J]. Science China Information Sciences, 2015, 58(3): 1-13.

[9] FAN Y H, WU X F, XU H Y, et al. Design of lateral control system for a hypersonic cruise missile[C]∥Proc.of the 21st AIAA International Space Planes and Hypersonics Technologies Conference, 2017: AIAA-2017-2111.

[10] JOON H Y, SEONG H S, JIN W H, et al. Singular perturbationlike approach to compensation of actuator dynamics effect in missile control[J]. IEEE Trans.on Aerospace and Electronic Systems, 2014, 50(4): 2417-2439.

[11] ZHANG K F, RAO D W, ZHU J B, et al. Real-time online compensation the nonlinearities and uncertainties in missile servo control system[C]∥Proc.of the 27th IEEE Chinese Control and Decision Conference, 2015:1333-1338.

[12] 陈罗婧,刘莉,于剑桥.双通道控制旋转导弹自动驾驶仪解耦控制研究[J]. 北京理工大学学报,2008,28(1): 11-14

CHEN L J, LIU L, YU J Q. Transform and coupling analysis of double-channel control rolling missile autopilot loop[J].Transactions of Beijing Institute of Technology, 2008, 28(1): 11-14.

[13] 毕艳超,姚晓先,宋晓东,等.双通道控制旋转导弹的舵机控制研究[J].弹箭与制导学报, 2014,34(2):25-28.

BI Y C, YAO X X, SONG X D, et al. The research on actuator control used for double-channel control of rolling missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(2): 25-28.

[14] 于剑桥,林凡,方正.自激振荡线性化舵机延迟补偿时间处理方法研究[J].兵工学报, 2009, 30(5):652-656.

YU J Q, LIN F, FANG Z. Research on the method to deal with delay compensation time of self-oscillation linear actuator[J]. Acta Armamentarii, 2009, 30(5):652-656.

[15] GARMELL P. Guided weapon control systems[M]. London: London Royal Military College of Science, 2003.

[16] MO B, GAO E Y, YANG S X. Research on spin rocket double-channel proportional control characteristics[C]∥Proc.of the IEEE International Conference on Innovative Computing, Information and Control, 2007.

[17] FORTWSCUE P W. Pitch/Yaw coupling due to roll of an axisymmetric missile with autopilot[J]. Aeronautical Quarterly, 1989, 33(2): 124-139.

[18] PHILIPPE W, FRIEDRICH L, DENIS B, et al. Wind tunnel tests and open-loop trajectory simulations for a 155 mm canards guided spin stabilized projectile[C]∥Proc.of the AIAA Atmospheric Flight Mechanics Conference, 2008: AIAA-2008-6881.

[19] PHILIPPE W. Stability analysis for canard guided dual-spin stabilized projectiles[C]∥Proc.of the AIAA Atmospheric Flight Mechanics Conference, 2009: AIAA-2009-5843.

[20] CHEN L F, LI L, YAO X X, et al. A study on actuator’s control hysteresis and corresponding countermeasures of spinning missile[C]∥Proc.of the 5th International Conference on Mechatronics and Control Engineering, 2016: 118-125.

[21] BI Y C, YAO X X, SONG X D. Influence of revolving angle measure precision and actuator performance on control force[J]. Applied Mechanics and Materials, 2013, 389: 765-769.

[22] XIANG C, BU X Z, YANG B. Three different attitude measurements of spinning projectile based on magnetic sensors[J]. Measurement, 2014, 47(1): 331-340.

[23] LÜ Q L, GAO X D, WANG X M, et al. The research on real-time calculation of projectile's roll angle based on geomagnetic detection[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(3): 30-31.

[24] WANG Z, GAO F Q, GAO M, et al. Roll angular velocity real-time tracking algorithm based on geomagnetic information with frequency-locked loop[C]∥Proc.of the International Conference on Civil, Materials and Environmental Sciences, 2015: 263-267.

[25] CAO H S, DU Y, WANG J H, et al. Detection technology of roll attitude based on geomagnetic signals and inertial trajectory study[J].Advanced Materials Research,2012,468-471:885-890.

[26] 王旭刚,王中原.弹体滚速和舵机时间常数对炮弹制导精度的影响[J].南京理工大学学报(自然科学版),2011,35(2):182-186.

WANG X G, WANG Z Y. Effect of roll angular velocity and actuator time constanton guidance precision of guided projectile[J].Journal of Nanjing University of Science and Technology,2011,35(2):182-186.

[27] YAO X X, LIN F. Frequency response computation and error analyses[J]. Journal of Beijing Institute of Technology, 1999, 8(4): 381-385.