拱桥吊杆涡激风振疲劳寿命评估

王祥真，芦 杰

（浙江省绍兴市交通工程质量安全监督站，浙江 绍兴 312000）

0 引 言

在钢管混凝土拱桥中，吊杆是重要的传力构件，由于其通常采用圆形截面，由此带来了涡激风振的问题。圆形断面在一定的雷诺数条件下会在与来流风向相互垂直的上下表面内产生交替脱落的漩涡以及涡激力，在这种涡激力的作用下吊杆产生往复振动。当吊杆整体刚度较大且基频频率较高时，涡振不易发生。当拱桥跨度较大、使用的吊杆长细比较大时，其基频降低较多；当吊杆的基频与漩涡脱落频率接近时，就会发生气流与结构之间的共振。在一定的风速范围内，两者还将相互锁定，并维持这种共振作用。如果风速稳定而持续，吊杆在这种往复荷载的长期作用下必将发生疲劳破坏，国内外已发生了多起吊杆遭受疲劳破坏的案例［1－4］，相关人员也进行了大量研究。余岭等［5］通过现场实测测定了各吊杆的低频振动模态参数及涡振特征参数，确定了吊杆产生涡振的风速锁定范围及最不利风向。刘慕广［6］对拱桥、桁架桥中常见的H型和矩形拱桥吊杆在大攻角下的风振特性及气动机理进行了风洞试验和理论研究。顾金钧等［7］、张龙奇等［8］也对H型吊杆的涡激风振开展了研究，指出了吊杆振动频率与涡振模态的对应关系，并设计制作了与频率相适应的TMD阻尼器。上述研究大多针对H型吊杆，圆形吊杆涡激风振如何计算虽然为广大学者所熟知，但设计单位、运营维护单位未曾系统性地了解和掌握。

1 涡激风振计算基本理论

1．1 圆形吊杆涡激风振发生原理

根据流体力学基本理论，空气既有质量，也有一定的黏性系数。在流动中，惯性力和黏性力同时存在，且是空气流动中影响最大的2个作用力，它们的相互关系成为确定出现哪种类型流动特性或现象的依据［9］。这个关系可用惯性力与黏性力之比——雷诺数Re来表示。当Re较大时，惯性效应起主要作用；当Re较小时，则黏性效应较强。其中，当40≤Re＜3×105时，上面的气流向下挤，形成下涡，下面的气流又向上挤，形成上涡，二者交替出现，且交替从圆柱体上脱落，以略低于周围流体的速度向下游移动，形成2列交替错开、旋向相反、间距保持不变的周期性脱落旋涡（图1）。在这种横风向涡脱的发生频率与拱桥吊杆的某阶振动频率较为接近时，就会发生持续的限幅涡激振动。

图1 亚临界范围圆柱体横向绕流

1．2 涡振风速区间的计算

为了描述这种尾流效应的显著规律，学者引入了斯脱罗哈数这一无量纲参数St来进行描述。

式中：U为来流风速；D为物体特征尺寸，取圆形断面直径；ns为漩涡脱落频率；St取决于被流体所包围的柱体形状，可通过风洞试验获得。

根据文献［10］可知，圆形断面St在0．2～0．21之间，本文取0．2。据式（1）计算不同风速下的旋涡脱落频率ns。

共振发生后，在一定的风速范围内，涡振都将持续发生。由文献［11］可知，涡振的锁定区范围在1．12～1．24，本 文 取 1．24。 当 风 速 处 于 Ucr～1．24Ucr之间时，涡振都会发生。因此，圆形吊杆发生涡振次数的多少，是由吊杆自振频率、外径和环境风场的风速共同决定的。

1．3 拉压作用下吊杆振动频率的修正

因拱桥吊杆内需要传递较大的内力，为考虑拉压荷载对吊杆频率的影响，根据文献［12］计算拉压作用下杆件固有的自振频率。

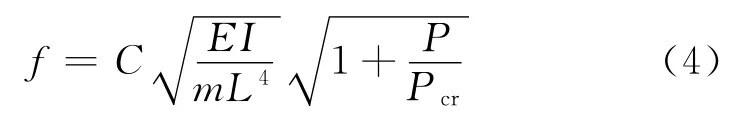
式中：f为吊杆的固有频率；E为吊杆的弹性模量；I为吊杆的惯性矩；m为吊杆单位长度的质量；L为吊杆的计算长度；P为吊杆的使用张力；Pcr为Euler临界荷载；C为吊杆两端支撑条件系数。不同支撑条件下C值相差较大，两端固支时C＝3．56，两端铰支时C＝1．57。

分析式（4）可知用于考虑吊杆拉压力对其频率的影响，其他阶次的振动频率也需要用这个系数进行修正。最终确定吊杆自振频率时，除代入圆形吊杆的相关截面特性外，还需准确代入恒载单独作用、恒活载共同作用下的实际吊杆拉力。

1．4 吊杆涡激力计算

由于此时考虑的是分布于吊杆上的涡激力，故需要将吊杆作为梁进行处理。梁的第j阶振型的广义运动方程为

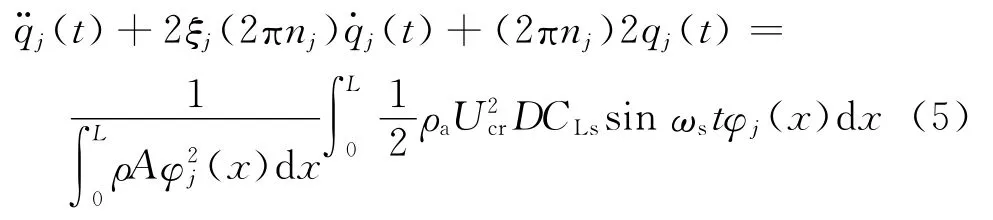
式中：φj（x）为第j阶振型；qj为广义坐标；ξj为阻尼比；nj为振动频率；CLs为升力系数，光圆截面可取0．22；ωs为旋涡脱落的圆频率；ρ为杆件质量密度；A为截面面积；t为时间；ρa为空气密度，通常取1．225kg·m－3。

某医院建筑面积为70488 m2,热源主要由3台3.9 t/h 柴油锅炉产生蒸汽，冬天通过中央空调供暖，夏天驱动溴化锂制冷机组制冷，蒸汽还常年用于消毒室的医疗器具消毒、手术室消毒、食堂热水供应、餐具消毒和浴室沐浴。空调系统冷源部分主要由2台2180 kW制冷量的吸收式溴化锂机组、1台3768 MJ(90万大卡)螺杆式制冷机组、378 kW制冷量的日立热泵空调机组和108 kW制冷量的开利热泵机组构成。其中吸收式溴化锂机组和螺杆制冷机组主要负责病房、门诊大楼的空调负荷，日立热泵空调机组主要负责手术室所需要的恒温恒湿空调，开利热泵机组主要负责产房的空调负荷。

方程右边即为作用在钢管杆件上的广义涡激力。共振情况下，方程（5）的解为

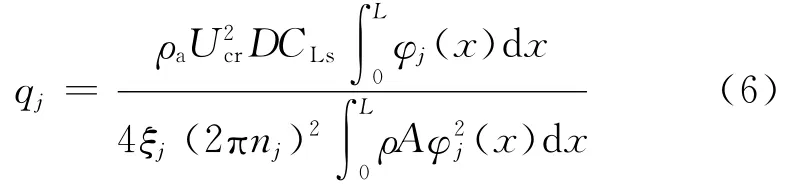
因而第j阶涡激共振的风振力为

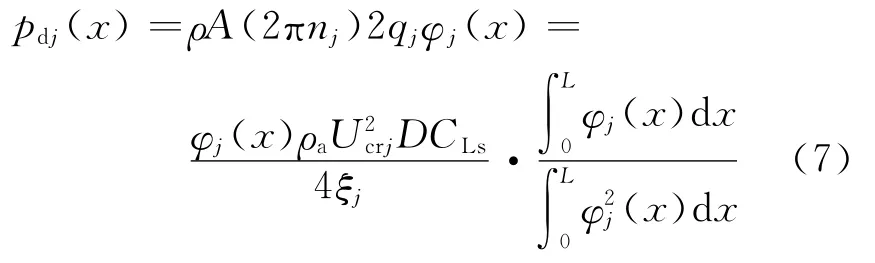
简化式（7），并对杆件长度积分，得到第j阶涡振共振的合力

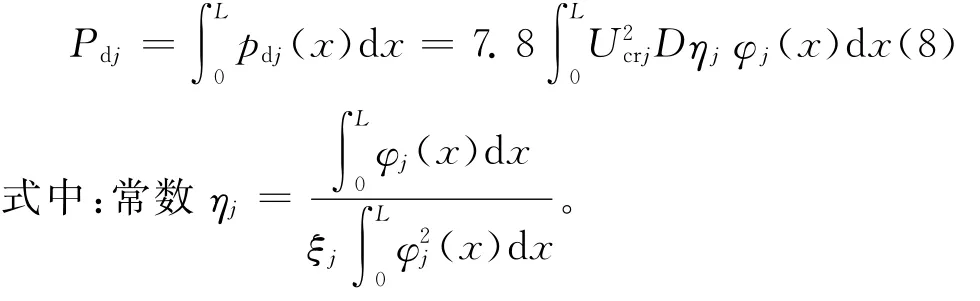
利用φ1（x）的函数式［13］得到两端固支、两端铰支2种杆端约束对应的η1值分别为1．32和1．27。

对式（8）沿钢管构件长度积分，得到作用在构件中间位置处的等效涡激力，两端固接时

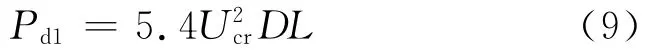
两端铰接时

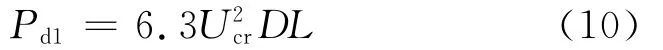
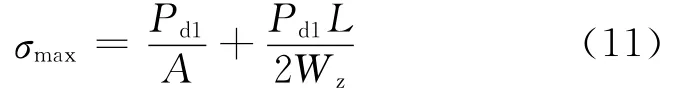
式中：A为吊杆截面面积；Wz为吊杆抗弯截面系数。

1．5 吊杆涡振疲劳寿命计算

根据《钢结构设计规范》（GB 50017—2003），微风共振钢管构件常幅疲劳的容许应力幅

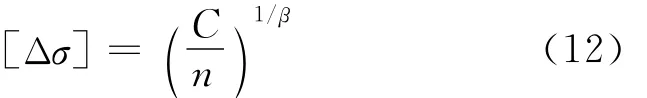
在等效涡激力弯剪共同作用下，其最大应力幅值σmax按照下式计算。

按第5类连接考虑，C的值为1．47×1012，β为3。应力循环次数nσ可按照下式进行估算。

在获取应力循环次数后，还需收集桥梁所在地的风速分布数据，确定在一年之中发生涡振的风速频次nu，则单纯考虑涡振作用下的吊杆疲劳寿命T按下式计算。

式中：ρv为发生涡振风速在全年风速中所占比例。

2 某钢管混凝土拱桥的工程背景

2．1 工程概况

本文算例选取的钢管混凝土系杆拱桥跨径40 m，拱圈轴心线为抛物线形，矢跨比为1／5。两道平行拱肋中心距为10．9m。主拱直径70cm，壁厚1．5cm，灌注混凝土标号为C40。系杆梁为90×130钢箱梁，壁厚1．2cm。沿桥梁跨径方向共设置了13道刚性吊杆，吊杆是直径20cm的钢管，壁厚1．5cm。风撑采用钢管混凝土结构，钢管直径为40cm，壁厚1cm。横梁为钢筋混凝土梁，其上铺置桥面板。大桥立面布置如图2所示。

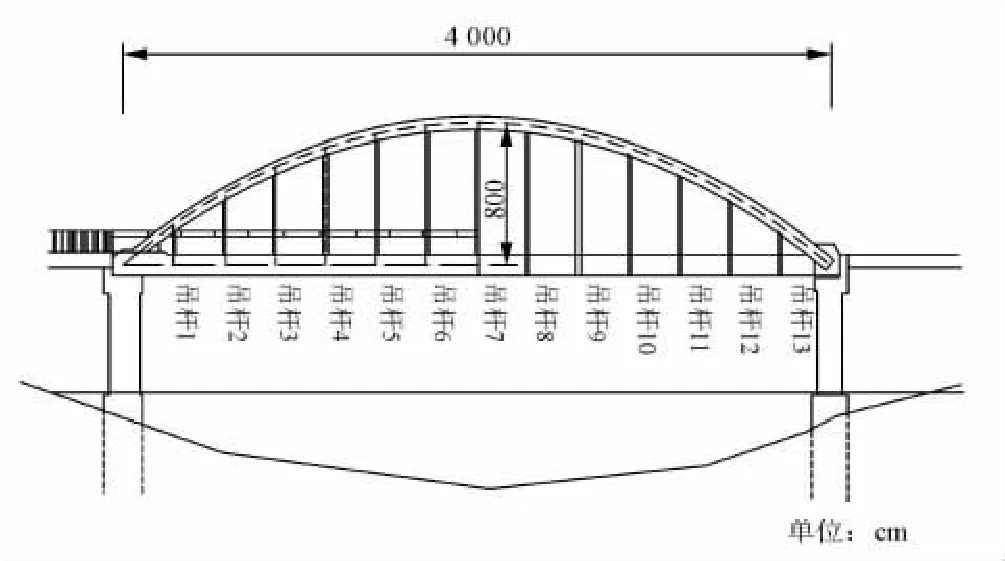
图2 大桥立面布置

2．2 吊杆内力与自振频率计算

在ANSYS中建立了钢管混凝土拱桥的有限元模型，用于分析吊杆在荷载作用下的内力［14－16］。拱桥吊杆内力分析模型如图3所示。经计算，得到拱桥在恒载及恒载与活载作用下各吊杆的内力，以及考虑内力影响后的自振频率，如表1所示。考虑到沿跨径中心线左右两侧的吊杆具有一定的对称性，仅给出了左侧7根吊杆的内力及频率。由表1可知：因桥梁跨径较小，吊杆长度较小，吊杆整体频率较高；因吊杆的欧拉临界荷载较大，荷载作用对杆件频率的影响可以忽略不计。

3 吊杆涡振疲劳计算

3．1 吊杆涡振起振临界风速计算

图3 拱桥吊杆内力分析模型

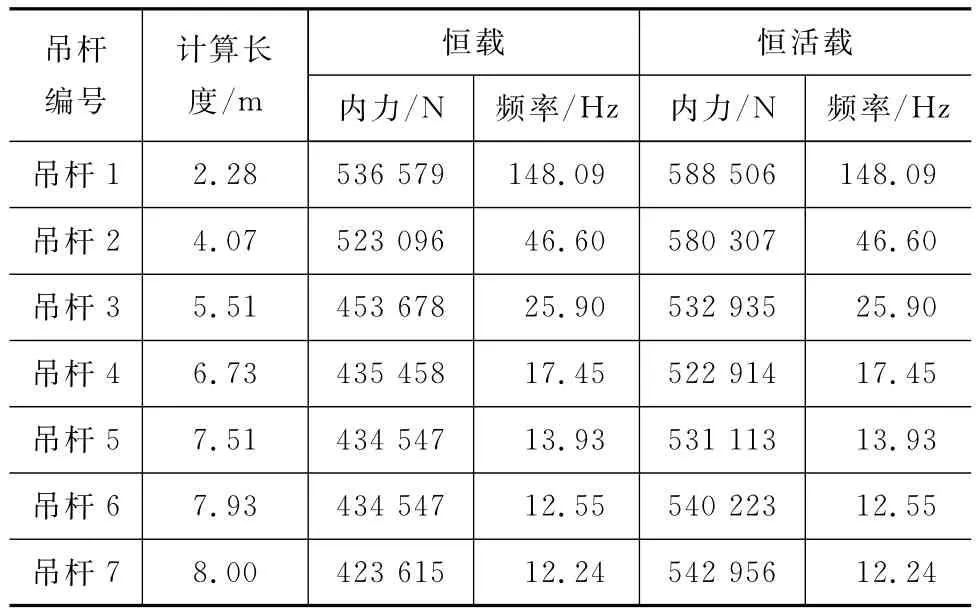
表1 在恒载及恒活载作用下各吊杆的内力及角振频率

根据吊杆气动外形尺寸，D取0．2m。对于本文拱桥吊杆而言，因其二阶涡振频率将会很高，涡振往往发生在一阶顺线向或横桥向频率附近，故吊杆频率取表1中的固有频率值，代入式（3）可得各吊杆涡振起振临界风速，并将1．24Ucr作为涡振风速上限。表2给出了各吊杆的涡振风速范围。

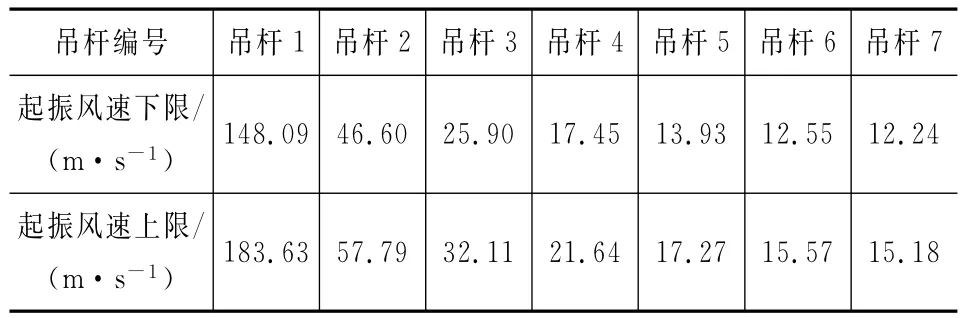
表2 各吊杆涡振风速范围

由表2可知，吊杆1～3的涡振风速下限较高，在自然界中不太可能发生涡振，只有吊杆4～7可能会发生涡振，后续涡激力及疲劳寿命计算仅针对这4根吊杆进行。

3．2 吊杆涡振疲劳应力计算

偏于安全地将吊杆两端取为铰接，按照式（10）计算吊杆4～7在等效涡激力作用下的应力σmax。等效涡激力按照作用在吊杆中部的集中力开展计算。表3给出了各吊杆的等效涡激力及其作用下的最大应力。

3．3 吊杆涡振疲劳寿命评估

要得到吊杆的疲劳寿命，必须获取桥梁所在地的自然风风速分布频次统计数据。图4给出了本文

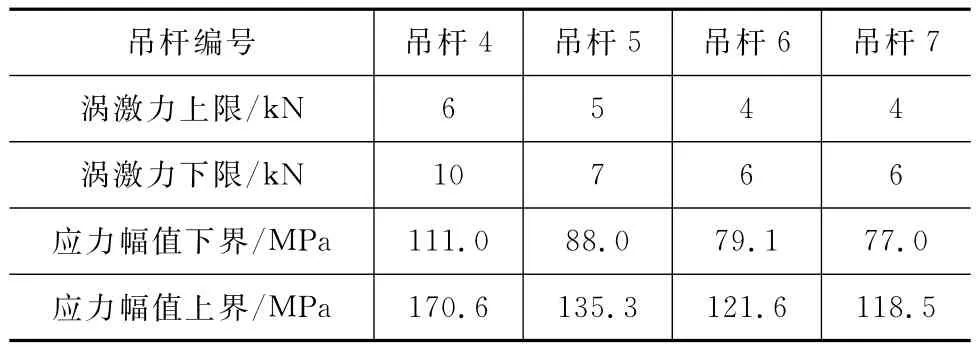
表3 各吊杆等效涡激力及最大应力幅值

所研究的拱桥所在地的风速分布百分比。基于表3给出的涡激应力幅值σmax，代入式（13）计算允许最大应力循环次数nσ［17］。基于表2给出的涡振风速范围及图4给出的风速分布百分比数据，计算各吊杆一年之中发生涡振的风速频次nu。

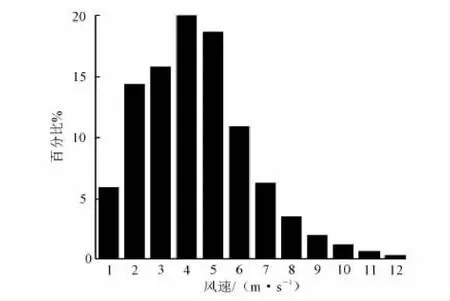
图4 桥梁所在地风速分布统计

表4给出了各吊杆的涡振风速发生频率及对应的涡振疲劳寿命。由表4可知，该拱桥吊杆的涡振风速均较高，在当地较低的自然风风速发生概率条件下，较少发生涡振，最终评估其涡振疲劳寿命不小于59年。

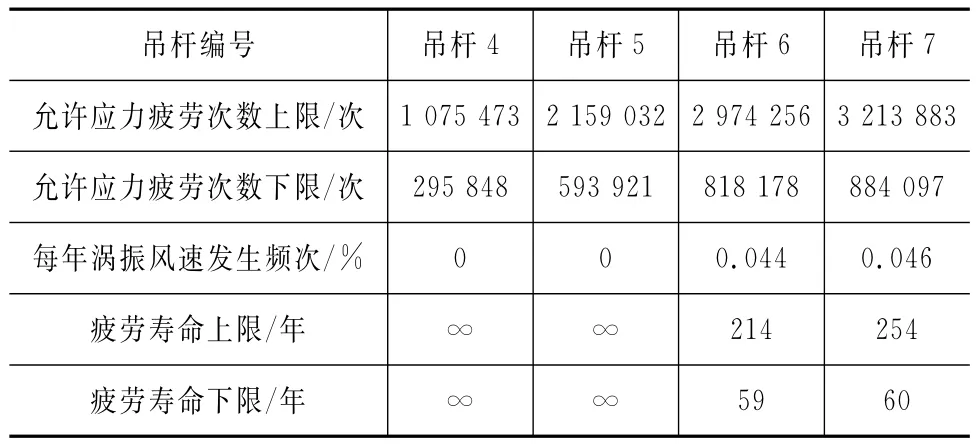
表4 各吊杆等效涡激力及最大应力幅值

4 结 语

本文基于涡激风振临界风速及涡激力计算的基本理论，建立了钢管混凝土拱桥模型，分析了吊杆内力与频率，收集了拱桥所在地的风速分布统计数据，最终对某钢管混凝土拱桥刚性吊杆的涡振疲劳寿命进行了评估。通过开展上述研究工作，得到以下研究结论。

（1）系统地给出了桥梁圆形吊杆涡振风速范围、涡激力及疲劳寿命的计算方法。

（2）因吊杆的欧拉临界荷载较大，荷载作用对杆件频率和涡振风速区间的影响可以忽略不计。

（3）在利用涡振发生的理想情况下，所研究拱桥全部吊杆的涡振疲劳寿命不小于59年；考虑自然界风场中湍流对涡振发生的抑制作用，该桥在使用寿命期限内不存在吊杆发生涡振疲劳破坏的风险。

［1］ 李冬生．拱桥吊杆损伤监测与健康诊断［D］．哈尔滨：哈尔滨工业大学，2007．

［2］ 吴 骏．公轨两用特大桥吊杆疲劳分析田［D］．长沙：中南大学，2008．

［3］ 王武勤，雷俊卿．桥梁失事案例剖析［C］∥中国土木工程学会．中国土木工程学会第九届年会论文集：工程安全及耐久性．北京：中国水利水电出版社，2000：265－269．

［4］ 方 兴，白 玲，刘 磊．南京大胜关长江大桥钢吊杆两端连接涡振疲劳性能的仿真分析［J］．铁道建筑，2011（3）：1－3．

［5］ 余 岭，顾金钧，汪正兴，等．大型桥梁吊杆涡振试验研究［J］．机械强度，1996（4）：16－20．

［6］ 刘慕广．两类大长细比桥梁构件的风振特性研究［D］．长沙：湖南大学，2009．

［7］ 顾金钧，赵煜澄，邵克华．九江长江大桥应用新型TMD抑制吊杆涡振［J］．土木工程学报，1994，27（3）：3－13．

［8］ 张龙奇．自然风作用下大跨钢桁拱桥刚性长吊杆减振措施研究［D］．成都：西南交通大学，2011．

［9］ 李 峰．输电塔典型节点钢管杆件涡激振动研究［D］．上海：同济大学，2008．

［10］ DENG H Z，JIANG Q，LI F，et al．Vortex－induced Vibration Tests of Circular Cylinders Connected with Typical Joints in Transmission Towers［J］．Journal of Wind ＆ Engineering，2011，99（10）：1069－1078．

［11］ ZHOU C Y，SO R M．LAM K．Vortex－induced Vibration of an Elastic Circular Cylinder［J］．Journal of Fluids and Structures，1999，13（2）：165－189．

［12］ 周家付．基于ANSYS的挖掘机连杆螺栓的疲劳寿命预测［J］．筑路机械与施工机械化，2011，28（1）：77－78，82．

［13］ 刘 静．基于ANSYS的路面冷再生机机架结构分析［J］．筑路机械与施工机械化，2012，29（11）：70－72．

［14］ 谢里阳，任俊刚，吴宁祥，等．复杂结构部件概率疲劳寿命预测方法与模型［J］．航空学报，2015，36（8）：2688－2695．

［15］ 雷宏刚，付 强，刘晓娟．中国钢结构疲劳研究领域的30年进展［J］．建筑结构学报，2010，31（S1）：84－91．

［16］ 刘文光，陈国平，贺红林，等．结构振动疲劳研究综述［J］．工程设计学报，2012，19（1）：1－8，24．

［17］ 周志刚．随机风作用下风力发电机齿轮传动系统动力学及动态可靠性研究［D］．重庆：重庆大学，2012．