平头弹低速冲击下薄钢板的穿甲破坏机理研究

徐伟， 侯海量， 朱锡， 陈长海， 李茂

(海军工程大学 舰船工程系， 湖北 武汉 430033)

0 引言

穿甲侵彻过程是非常复杂的力学行为，弹靶相互作用影响因素非常复杂，例如弹靶材料特性及其强度比、弹体几何形状和初始速度、靶板厚度和组合方式以及侵彻角度等均会对弹体的侵彻性能和靶板的失效模式产生较大影响。文献[1-4]针对不同头部形状弹体的侵彻性能开展了试验和数值研究。Gupta等[3]指出：当靶板较薄时，平头弹正冲击下靶板出现剪切冲塞失效；而球头弹正冲击下靶板首先出现拉伸变薄，随后在局部区域形成裂纹，裂纹的进一步扩展造成靶板失效，尖头弹正冲击下则会出现花瓣开裂。文献[5-11]深入研究了平头弹冲击下靶板的响应。Woodward[5]通过计算靶板的剪切功、弯曲变形能以及薄膜拉伸变形能，提出了亚弹速范围内简支薄板在钝头弹正冲击下的理论公式，但是其失效准则未能充分考虑拉伸与剪切应力的共同作用。Wen等[6-8]则先后分析了简支梁和板在平头弹低速冲击下的响应，其根据准静态理论分析了低速冲击下薄板的“载荷—位移”关系式，据此得到了钝头弹冲击下靶板吸能的解析解，其在弹体初速较小时吻合情况较好。国内学者针对平头弹开展了广泛而深入的研究，例如：Chen等[9-11]先后分析了弹体在不同初速下正冲击不同厚度靶板的侵彻特性，其剪切模型在剪切破坏中还考虑了结构拉伸与弯曲，在内嵌模型中则采用了动态膨胀理论，其理论模型与试验结果吻合较好，该研究成果对建立平头弹正侵彻钢板的理论模型具有重要意义；蒋志刚等[12]通过理论分析得到了塑性金属靶板在刚性弹冲击下最小穿透能量的半理论、半经验公式；潘建华等[13]分析了高速冲击下绝热剪切模型与低速冲击Wen-Jones模型转化的临界条件；其他学者则针对弹体冲击下靶板的失效模式、破口大小、吸能特性，开展了广泛的研究[14-18]，并对比了双层与单层靶板之间的吸能特性[19]，其研究成果对于建立适用广泛的理论模型具有重要作用。然而上述模型中均假定弹体为刚性，其适用于弹体没有变形或变形可以忽略不计的情形，但是当弹体材料与靶板材料强度比较小时，弹体会出现较大变形，例如文献[20]针对侵彻过程中弹靶的耦合作用进行了理论分析，得出了非刚性钝头弹侵彻靶板时弹体的墩粗变形理论模型，但是其研究侧重于弹体的理论分析，对于靶板变形和弹体剩余速度未曾提及。本文通过弹道冲击试验，结合数值仿真以及理论分析方法，同时参考文献[20]中弹体变形的理论模型，探讨了平头弹低速冲击下弹体和薄板的变形与破坏(试验初速在300～500 m/s之间，属于低速范畴[21])，分析了侵彻过程中靶板的受力特征，并讨论了靶板的失效模式，根据试验结果确定了碟形区最终变形挠度的拟合函数，并对弹体和靶板的塑性变形能进行了理论分析，利用能量守恒原理建立了平头弹低速侵彻薄钢板的剩余速度计算模型。

1 试验设计

弹道试验采用14.5 mm口径滑膛弹道枪，通过火药发射，弹体初始速度通过火药量控制。弹体初速采用激光测速系统(1号和2号光幕靶)得到。同时采用高速摄影仪记录弹体的侵彻过程，用于分析弹体侵彻靶板后的姿态变化。靶板为Q235钢，正方形靶板尺寸为400 mm×400 mm×2 mm，靶板上呈圆形均匀分布12个螺栓孔，圆形半径为185 mm. 通过12个M8螺栓固定于靶架上，靶架上的圆形开孔半径为175 mm，即靶板的自由跨度为350 mm. 试验采用长径比l0/dp为1.33的平头弹，弹体直径dp为14.5 mm，长度l0为19.3 mm，质量为25 g，弹体材料为经淬火处理的45号钢，弹体和靶板的准静态力学性能参数如表1所示。

表1 弹丸和靶板的力学性能参数[22]

试验初速在300～500 m/s之间，主要用于模拟战斗部侵彻舰船防护外板的情形。

2 数值计算模型

采用非线性有限元分析软件ANSYS/LS-DYNA建立三维有限元模型，弹体和靶板均采用六面体单元。靶板中心4倍弹径内网格尺寸为0.75 mm，4倍弹径外采用放射性网格，靶板在厚度方向划分8个单元。弹体与靶板之间采用面面侵彻接触。靶板材料采用双线性弹塑性本构模型，材料的应变率效应由Cowper-Symonds模型描述。

(1)

(2)

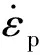
材料失效应变εf由下述方程描述：

(3)

式中：D1～D5为材料常数；σeff为von Mises等效应力；σh为材料在三向应力状态下的静水压力。当破坏参数Df达到1时，材料发生失效，

Df=∑(Δεp/εf),

式中：εf为失效应变。

弹体和靶板材料参数如表2所示。

表2 弹丸和靶板材料参数[22]

3 试验及仿真结果

表3为弹道试验得到的初始速度和剩余速度。侵彻角为90°，仿真值通过读取弹体PART获得。

表3 试验和仿真结果及主要参数

4 结果分析

4.1 弹体变形

本文弹体直径与靶板厚度比dp/ht为7.25，然而弹体与靶板材料的屈服强度比为1.42，弹体侵彻金属靶板过程中，在弹体头部产生向尾部传播的压缩波，由于弹靶作用过程较长，弹体在侵彻过程中同样出现一定程度的变形。弹体以初速v0撞击靶板后，弹体尾端速度保持不变，而头部则以速度u向靶板不断侵彻，由于在本试验弹速范围内，(v0-u)小于弹体材料中的塑性波速cp[23]，因而在弹靶接触界面与向尾端传播的压缩波阵面间形成一个“塑性区”，该塑性区内的弹体材料由于惯性效应由轴向流向弹体头部，受靶板的阻碍作用，弹体头部材料沿径向塑性流动，从而形成类似“泰勒”撞击的墩粗变形。图1为试验后收集的弹体变形破坏形貌，由图1可知，弹体头部均发生了一定程度的墩粗变形，随着弹体初始速度的增加，弹体墩粗变形也不断变大。

4.2 破坏过程及机理

为了进一步分析弹靶作用过程及变形机理，提取靶板中面节点的法向与径向位移并绘制曲线如图2所示。其中sz和sr分别为法向(弹体运动方向)和径向(垂直于弹体运动方向)位移，r′=r/rp，r为节点距撞击中心的距离，rp为弹体半径。正侵彻条件下，弹体运动垂直于靶板，弹靶之间作用力完全对称，相应地靶板响应在各个方向也完全对称，取靶板某一方向进行分析。由图2可知：弹靶接触初期，2 μs时刻，弹体紧贴靶板沿法向运动。在1倍弹径内靶板的法向位移与弹体的平头面完全贴合，其径向位移基本为0；径向节点由于弹体挤压作用，出现较大横向位移(此处径向位移为正值，即由弹体撞击区向外运动)在1倍弹径附近，节点的法向位移基本为0，径向则由于弹体的挤压作用而出现较大的横向位移(此处径向位移为正值，即由弹体撞击区向外运动)；在1倍弹径以外，应力波均未能到达，靶板的法向位移为0，径向位移也基本为0. 随着弹靶作用过程的继续，弹体速度降低，压缩剪切作用减弱，靶板的拉伸作用逐渐增强，10 μs时刻，在1倍弹径内靶板的法向位移与弹体的平头面并不完全贴合，径向由于拉伸作用而出现较大的横向位移；在1倍弹径附近，节点的法向与径向位移均较大；在1倍弹径以外，靶板的法向位移较大，由于面内拉伸作用径向位移较大，其中拉伸位移以1倍弹径为分界点，1倍弹径以内拉伸位移为正(由内向外)，1倍弹径以外拉伸位移为负(由外向内)。当弹体穿透靶板后，靶板仍具有一定速度，其法向位移不断增加，但增加速度不断降低最后趋于稳定。在穿透初期，20 μs时刻，靶板的法向运动使得其进一步发生碟形变形，在1～1.5倍弹径范围内，由于靶板的弯曲作用节点径向位移为正；1.5倍弹径以外，弯曲变形较小结构以拉伸变形为主，因而节点径向位移为负，但随着靶板速度的降低和r′的增加，径向位移逐渐减小。

由图3可知，正应力与剪应力在边界产生反射波之前呈现明显的波形传播规律，根据不同时刻波峰传播的距离，确定正应力和剪应力的波速分别为5.19×103m/s和3.22×103m/s. 靶板材料的弹性模量Et为210 GPa，密度ρt为7.8×103kg/m3，泊松比υ为0.3，从理论上分析[23]可知：

二维应力状态下膨胀波波速为

剪切波速为

由此可知，根据广义应力图计算所得应力波速和理论值吻合较好，即该广义应力表示法能有效反映结构的受力特征。

1)压缩剪切变形阶段：从弹体接触靶板开始，弹体被减速，与其接触的靶板被加速，此时弹靶接触界面的速度最高，产生的压缩应力最大，远超过钢板的动态压缩强度。由于接触区材料被加速，沿面内传播的剪切波使与接触区相邻的靶材(以下称为协变区)也获得一定的横向速度，接触区与协变区之间较大的速度差导致接触边缘区出现剪切变形，靶板在碰撞的局部区域发生变形失效，同时弹体发生略微的墩粗变形，如图4(a)所示。该阶段1倍弹径内广义正应力较大(且为负值)，即为由内向外的压缩应力；1倍弹径处广义剪切应力值较大，由于应力波的传播需要一定时间，接触区各层的径向正应力值并不相同，故在1倍弹径内板中的广义弯矩值较大。

2)碟形变形阶段：随着弹体运动，接触区的靶板材料法向速度不断增加，弹体动能不断降低。当压缩波传播至靶板背面时，背面无约束，压缩波反射并形成拉伸波。拉伸波形成后在靶板厚度方向上沿弹体侵彻相反方向传播，当拉伸波与弹靶接触界面相遇时，靶板压缩变形结束。在此过程中，沿面内传播的剪切波使协变区的范围以及靶材速度不断增加，此时接触区的靶材速度降低，协变区的靶材速度增加，二者速度差不足以继续使靶材发生剪切失效，但是接触区和协变区的靶材同样具有一定的法向速度，靶板继续发生横向碟形变形(以下协变区因其碟形变形特征而简称碟形区)。如图4(b)所示，该阶段靶板面内的拉应力较大，同时由于横向速度影响，面内的弯矩值也较大，接触区与协变区的速度差使得接触区边缘存在剪应力，但是剪应力范围和幅值较上一阶段已大大减弱。

3)拉伸与剪切混合失效阶段：随着弹体运动的法向速度进一步降低，同时由于剪切波和塑性波的作用，碟形区的靶材速度进一步增加，因而接触区与碟形区靶材的速度差进一步降低，弹体法向运动的同时带动靶板材料一起运动，整个接触区和碟形变形区靶板材料会产生拉伸变形，接触区边缘由于速度差存在剪切变形，拉应力和剪应力的联合作用，使靶板材料产生失效裂纹(拉伸与剪切混合失效)，如图4(c)所示，碟形区由于法向速度的影响产生碟形变形。该阶段1倍弹径内(接触区)单元的广义径向膜力较大；由于裂纹的形成与扩展，使1倍至2倍弹径处单元的广义剪切应力较大；1倍弹径以外(碟形区)单元的广义膜力和弯矩均较大。

4)弹体贯穿阶段：随着弹体的进一步运动，裂纹逐渐扩展形成直径近似于弹径的帽形失效块，同时靶板进一步发生碟形变形。该阶段主要是靶板动能转换为靶板变形能，由于靶板法向挠度增加，接触区附近靶材不断扩张，因而径向弯矩和膜力仍较大，如图4(d)所示。

4.3 靶板失效模式

根据上述分析可知，弹靶接触初期主要为弹体的压缩墩粗和靶板的剪切失效，随后由于法向速度降低，靶板出现拉伸和弯曲变形，最后由于剪切和拉伸应力的联合作用，靶板发生失效，上述各作用力大小和作用时间因弹体初速的不同而存在一定差异，相应地产生不同的穿甲破坏模式。

当速度较小时(小于弹道极限)，接触初期产生较小的剪切变形后靶板便出现碟形变形，由于初始速度较小，弹体未能穿透靶板，接触区出现部分剪切失效和拉伸变形，非接触区为碟形变形，相应的失效模式为局部剪切—碟形变形失效模式，如图6(a)所示。当初始速度大于弹道极限时，弹体穿透靶板，弹靶接触初期同样产生剪切变形，随后靶板出现较大的碟形变形，接触区出现较大程度的拉伸变形，在拉应力和剪应力的联合作用下弹体最终穿透靶板，非接触区出现较大程度的碟形变形，相应的失效模式为带有碟形变形的拉伸与剪切混合失效模式，如图6(b)所示。当初始速度远大于弹道极限时，弹体穿透靶板，同样出现带有碟形变形的拉伸与剪切混合失效模式，只是碟形变形的幅值与范围变小，拉伸作用弱化、剪切失效更明显。图6(c)、图6(d)为工况序号5和工况序号6侵彻下靶板失效的试验图。由图6可知，平头弹低速侵彻下靶板的主要失效模式为带有碟形变形的拉伸与剪切混合失效模式，不同初始速度下仅是作用范围和变形大小以及靶板失效时拉伸和剪切作用大小不同。

图7为不同初始速度下各靶板沿径向各点处的变形挠度值及整体变形轮廓，图7中纵坐标w为变形挠度值。由图7可知，在一定速度范围内，不同初始速度下非接触区的整体变形大体相同，仅变形幅值不同，变形幅值随着初始速度的增加渐趋于稳定。确定靶板的变形位移场或速度场函数是建立剩余速度理论模型的基础，本文采用指数衰减函数对碟形变形进行拟合，结果显示其与试验数据吻合较好，因而平头弹正侵彻下靶板的法向变形函数可近似表达为

w=w0e-a(r-rp)，r>rp，

(4)

式中：w0为靶板的变形幅值；a为靶板变形系数；r为节点距撞击中心的距离；rp为弹体半径。

需要指出的是，指数函数趋零速度缓慢，而靶板在一定弹径外其挠度基本为0，因而在一定弹径外其拟合效果并不理想，但当弹径超过一定范围后，靶板变形较小，相应的吸能也减小，其变形挠度和吸能分析基本可以忽略不计。

4.4 塞块形状

弹体穿透靶板时，在靶板上形成直径近似于弹径的帽形失效块，如图8所示。

4.5 剩余速度

平头弹低速冲击下能量耗散于弹体变形、塞块形成和靶板变形，假设弹体穿透靶板后塞块与弹体一起运动，即塞块和弹体的剩余速度相同，根据能量守恒原理可知：

(5)

式中：mp为弹体质量；Epp为弹体的塑性变形能；Etp为靶板的塑性变形能；Es为剪切冲塞能；mg为塞块质量；vr为剩余速度，

(6)

根据上述弹体变形分析可知，弹体墩粗变形所消耗的能量为

(7)

式中：dp为弹体直径；σdp为弹体动态屈服应力；le为弹体塑性区长度。文献[20]针对柱形平头弹墩粗变形的理论，分析给出了考虑弹体与靶板同时变形的弹体塑性区长度。文献[20]指出，随着λ值的增大，弹体最终的变形区长度随之增加，最后趋于稳定，如图9所示，其中纵坐标为无因次变量le/l0，l0为弹体原长度。

图9中λ值为

(8)

式中：ρp为弹体密度；系数k的表达式为

(9)

ρt为靶板密度，cet为靶板弹性波速，ρp为弹体密度，cep为弹体弹性波速。

弹体侵彻过程中的剪切功为

Es=2πreτdthtδs,

(10)

式中：re为环形剪切带的半径，可取弹体外径；τdt为动态剪切强度，可取τdt=0.5σdt，σdt为动态屈服强度；ht靶板厚度；δs为剪切带宽度，由文献[8]得

(11)

靶板的塑性变性能主要为非接触区靶板碟形变形所消耗的能量[15]，其由3部分组成：

Etp=Erb+Eθb+Erm,

(12)

式中：Erb为径向弯曲变形能；Eθb为环向弯曲变形能；Erm为径向拉伸应变能。

(13)

式中：rj为侵彻过程结束时塑性铰距撞击中心的距离；kr为非接触区径向曲率，

(14)

M为非接触区靶板单位长度的动态极限弯矩，

(15)

动态屈服强度采用Cowper-Symonds模型[24]

(16)

(17)

(18)

(19)

式中：kθ为非接触区的环向曲率，εr为径向应变，

(20)

表4为本文理论计算所得弹体剩余速度与弹道冲击试验值的对比结果，其中变形幅值w0通过测量靶板变形获得，靶板变形系数a根据拟合结果获得。根据实测结果可知，10倍弹径外靶板的变形挠度几乎为0，故上述rj取10rp.

表4 弹体剩余速度理论值与试验值对比

注：上标1表示考虑弹体变形能，上标2表示不考虑弹体变形能。

由表4可知：本文理论计算模型与试验结果吻合较好；上述各工况试验误差均在10%以内；如果不考虑弹体变形能，则理论值与试验值的误差较大，相应的理论方法不能有效预估弹体剩余速度，也充分说明了当弹体与靶板材料强度相差较小时，弹体的变形不能忽略。

5 结论

本文通过弹道冲击试验并结合数值模拟及理论分析，从弹体变形、靶板穿甲过程和变形机理及破坏模式、塞块形状、弹体剩余速度等方面，研究了平头弹低速侵彻强度比相当的薄板时弹道特性，得出主要结论如下：

1)当平头弹侵彻强度比相当的靶板时弹体头部会出现一定程度的墩粗变形，弹体的塑形变形能不可忽略。

2)根据靶板受力特征，可将平头弹侵彻金属薄板的穿甲破坏分为4个阶段，即压缩剪切变形、碟形变形、拉伸与剪切混合失效和弹体贯穿阶段。

3)当初速小于弹道极限时，靶板失效模式为局部剪切—碟形变形；当初速大于弹道极限时，其失效模式为带有碟形变形的拉伸与剪切混合失效模式。初速较小时拉伸作用较为明显，初速较大时剪切作用更大。

4)根据能量守恒原理建立的平头弹低速侵彻薄板的剩余速度计算模型，其理论计算值与试验结果吻合较好，有效验证了理论模型的适用性。

参考文献(References)

[1] Borvik T, Langseth M, Hopperstad O S, et al. Perforation of 12 mm thick steel plates by 20 mm diameter projectiles with flat, hemispherical and conical noses: part I: experimental study[J]. International Journal of Impact Engineering, 2002, 27(1): 19-35.

[2] Borvik T, Hopperstad O S, Berstad T, et al. Perforation of 12 mm thick steel plates by 20 mm diameter projectiles with flat, hemispherical and conical noses: part II: numerical simulations[J]. International Journal of Impact Engineering, 2002, 27(1): 37-64.

[3] Gupta N K, Iqbal M A, Sekhon G S. Effect of projectile nose shape, impact velocity and target thickness on deformation behavior of aluminum plates[J]. International Journal of Solids and Structures, 2007, 44(10): 3411-3439.

[4] 余庆波，郭焕果，张田育子，等. 不同头形刚性弹丸侵彻钢靶力学行为[J]. 北京理工大学学报, 2017, 37(4): 331-336.

YU Qing-bo, GUO Huan-guo, ZHANG Tian-yuzi, et al. Dynamic behavior of non-deformation projectile with different nose shape penetrating steel plate [J]. Transactions of Beijing Institute of Technology, 2017, 37(4): 331-336. (in Chinese)

[5] Woodward R L. A structural model for thin plate perforation by normal impact of blunt projectiles[J]. International Journal of Impact Engineering, 1987, 6(2): 129-140.

[6] Wen H M, Reddy T Y, Reid S R. Deformation and failure of clamped beams under low speed impact loading[J]. International Journal of Impact Engineering, 1995, 16(3): 435-454.

[7] Wen H M. Deformation and perforation of clamped work-hardening plates struck transversely by blunt missiles[J]. Nuclear Engineering and Design, 1996, 160(1/2): 51-58.

[8] Wen H M, Jones N. Low velocity perforation of punch-impact-loaded metal plates[J]. Journal of Pressure Vessel Technology, 1996, 118(2): 181-187.

[9] Chen X W, Li Q M. Shear plugging and perforation of ductile circular plates struck by a blunt projectile[J]. International Journal of Impact Engineering, 2003, 28(5): 513-536.

[10] Chen X W, Zhou X Q, Li X L. On perforation of ductile metallic plates by blunt rigid projectile[J]. European Journal of Mechanics A/Solids, 2009, 28(2): 273-283.

[11] 陈小伟，梁冠军，姚勇，等. 平头弹穿透金属靶板的模式分析[J]. 力学学报, 2009, 41(1): 84-89.

CHEN Xiao-wei, LIANG Guan-jun, YAO Yong, et al. Perforation modes of metal plates struck by a blunt rigid projectile[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(1): 84-89.(in Chinese)

[12] 蒋志刚, 曾首义， 周建平. 金属薄靶板冲塞破坏最小穿透能量分析刚性平头弹[J]. 工程力学, 2004, 21(5): 203-208.

JIANG Zhi-gang, ZENG Shou-yi, ZHOU Jian-ping. Analyses of critical impact energy for plugging failure of thin metallic plates[J]. Engineering Mechanics, 2004, 21(5): 203-208. (in Chinese)

[13] 潘建华, 文鹤鸣. 平头弹丸正撞击下延性金属靶板的破坏模式[J]. 高压物理学报, 2007, 21(2): 157-164.

PAN Jian-hua, WEN He-ming. Failure modes of ductile metal plates under normal impact by flat-ended projectiles[J]. Chinese Journal of High Pressure Physics, 2007, 21(2): 157-164. (in Chinese)

[14] 邓云飞, 张伟, 孟凡柱，等. Q235钢单层板对平头刚性弹抗穿甲特性研究[J]. 振动与冲击, 2015, 34(2): 74-78.

DENG Yun-fei, ZHANG Wei, MENG Fan-zhu, et al. Ballistic resistance of Q235 steel monolithic plates impacted by rigid blunt-nosed projectiles[J]. Journal of Vibration and Shock, 2015, 34(2): 74-78. (in Chinese)

[15] 侯海量, 朱锡, 李伟, 等. 低速大质量球头弹冲击下薄板穿甲破坏机理数值分析[J]. 振动与冲击, 2008,27(1): 40-45.

HOU Hai-liang, ZHU Xi, LI Wei, et al. Numerical analysis of perforation mechanism for a thin plate subjected to impact by hemispherical-nosed projectiles with low velocity[J]. Journal of Vibration and Shock, 2008,27(1): 40-45. (in Chinese)

[16] 陈长海，朱锡，侯海量，等. 球头弹丸速冲击下薄板大变形的理论计算[J]. 华中科技大学学报：自然科学版, 2012, 40(12): 88-93.

CHEN Chang-hai, ZHU Xi, HOU Hai-liang, et al. Theoretical calculation of large deformation for thin plate impacted by hemispherical-nosed projectile with low velocity[J]. Journal of Huazhong University of Science & Technology:Natural Science, 2012, 40(12): 88-93. (in Chinese)

[17] Iqbal M A, Tiwari G, Gupta P K,et al. Ballistic performance and energy absorption characteristics of thin aluminium plates[J]. International Journal of Impact Engineering, 2015, 77(3): 1-15.

[18] 司马玉州，肖新科，王要沛,等. 7A04-T6高强铝合金板对平头杆弹抗侵彻行为的试验与数值模拟研究 [J]. 振动与冲击, 2017,36(11): 1-7.

SIMA Yu-zhou, XIAO Xin-ke, WANG Yao-pei, et al. Test and numerical simulation for anti-penetrating behavior of a high strength 7A04-T6 aluminium alloy plate against a blunt projectile’s impact[J]. Journal of Vibration and Shock, 2017,36(11): 1-7. (in Chinese)

[19] 刘兵, 陈小伟. 平头弹穿透间隙式双层靶的穿甲模式[J]. 爆炸与冲击, 2016, 36(1): 24-30.

LIU Bing, CHEN Xiao-wei. Perforation modes of double-layered plates with air space struck by a blunt rigid projectile[J]. Explosion and Shock Waves, 2016, 36(1): 24-30. (in Chinese)

[20] 张晓晴, 杨桂通, 黄小清. 柱形平头弹体墩粗变形的理论分析[J]. 华南理工大学学报：自然科学版, 2005, 33(1): 32-36.

ZHANG Xiao-qing, YANG Gui-tong, HUANG Xiao-qing. Theoretical analysis of the mushrooming deformation of flattened cylindrical projectile[J]. Journal of South China University of Technology:Natural Science Edition 2005, 33(1): 32-36. (in Chinese)

[21] 赵文宣.终点弹道学[M].北京:兵器工业出版社，1989.

ZHAO Wen-xuan. Terminal ballistics[M].Beijing: Publishing House of Ordnance Industry,1989.(in Chinese)

[22] 侯海量. 大型舰船水上舷侧结构抗毁伤机理研究[D]. 武汉：海军工程大学，2006.

HOU Hai-liang. Study on mechanism of damage-resistant of large scale surface warship top side structure[D].Wuhan: Naval University of Engineering, 2006. (in Chinese)

[23] 王礼立. 应力波基础[M]. 北京：国防工业出版社，2005.

WANG Li-li. Foundation of stress waves[M].Beijing: National Defense Industry Press, 2005. (in Chinese)

[24] 朱锡，张振华，梅志远，等. 舰船结构毁伤力学[M]. 北京：国防工业出版社，2013.

ZHU Xi, ZHANG Zhen-hua, MEI Zhi-yuan, et al. Damage mechanics of warship structure subjected to explosion[M]. Beijing: National Defense Industry Press, 2013. (in Chinese)